26.4: Métodos basados en caracteres

Figura 26.14: Una visión general de los métodos basados en caracteres

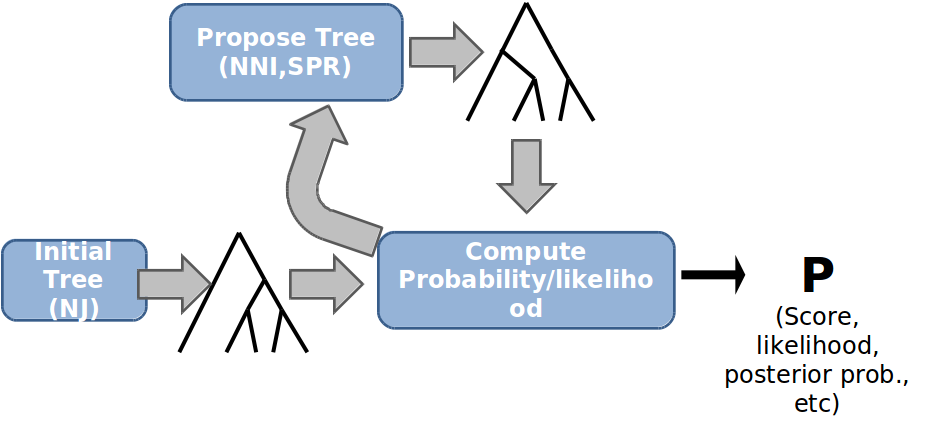
En los métodos basados en caracteres, el objetivo es crear primero un algoritmo válido para puntuar la probabilidad de que un árbol dado produzca las secuencias observadas en sus hojas, luego buscar a través del espacio de posibles árboles un árbol que maximice esa probabilidad. Buenos algoritmos para la puntuación de árboles, y aunque la búsqueda en el espacio de los árboles es teóricamente NP-dura (Debido a la gran cantidad de árboles posibles), los métodos de búsqueda heurística tratables pueden en muchos casos encontrar buenos árboles. Primero discutiremos los algoritmos de puntuación de árboles, luego las técnicas de búsqueda.

Apuntar

Hay dos algoritmos principales para la puntuación de árboles. El primer enfoque, que llamaremos reconstrucción de parsimonia, se basa en la navaja de Occam, y puntúa una topología basada en el número mínimo de mutaciones que implica, dadas las secuencias (conocidas) en las hojas. Este método es simple, intuitivo y rápido. El segundo enfoque es un método de máxima verosimilitud que puntúa árboles modelando explícitamente la probabilidad de observar las secuencias en las hojas dada una topología de árbol.

Parsimonia

Conceptualmente, este método es sencillo. Simplemente asigna un valor de para cada par de bases en cada nodo ancestral de tal manera que se minimiza el número de sustituciones. La puntuación es entonces solo la suma sobre todos los pares de bases de ese número mínimo de mutaciones en cada par de bases. (Recordemos que el objetivo final es encontrar un árbol que minimice ese marcador.)

Para reconstruir las secuencias ancestrales en los nodos internos del árbol, el algoritmo primero explora las secuencias foliares (conocidas), asignando un conjunto de bases en cada nodo interno en función de sus hijos. A continuación, itera hacia abajo en el árbol, escogiendo bases de los conjuntos permitidos en cada nodo, esta vez en función de los padres del nodo. A continuación se ilustra este algoritmo en detalle (tenga en cuenta que hay 2N-1 nodos totales, indexados desde la raíz, de tal manera que los nodos hoja conocidos tienen índices N-1 a 2N-1):

Figura 26.15: Puntuación de parsimonia: unión e intersección

Figura 26.16: Rastreo de parsimonia para encontrar neucleótidos ancestrales

Figura 26.17: Puntuación de parsimonia por programación dinámica

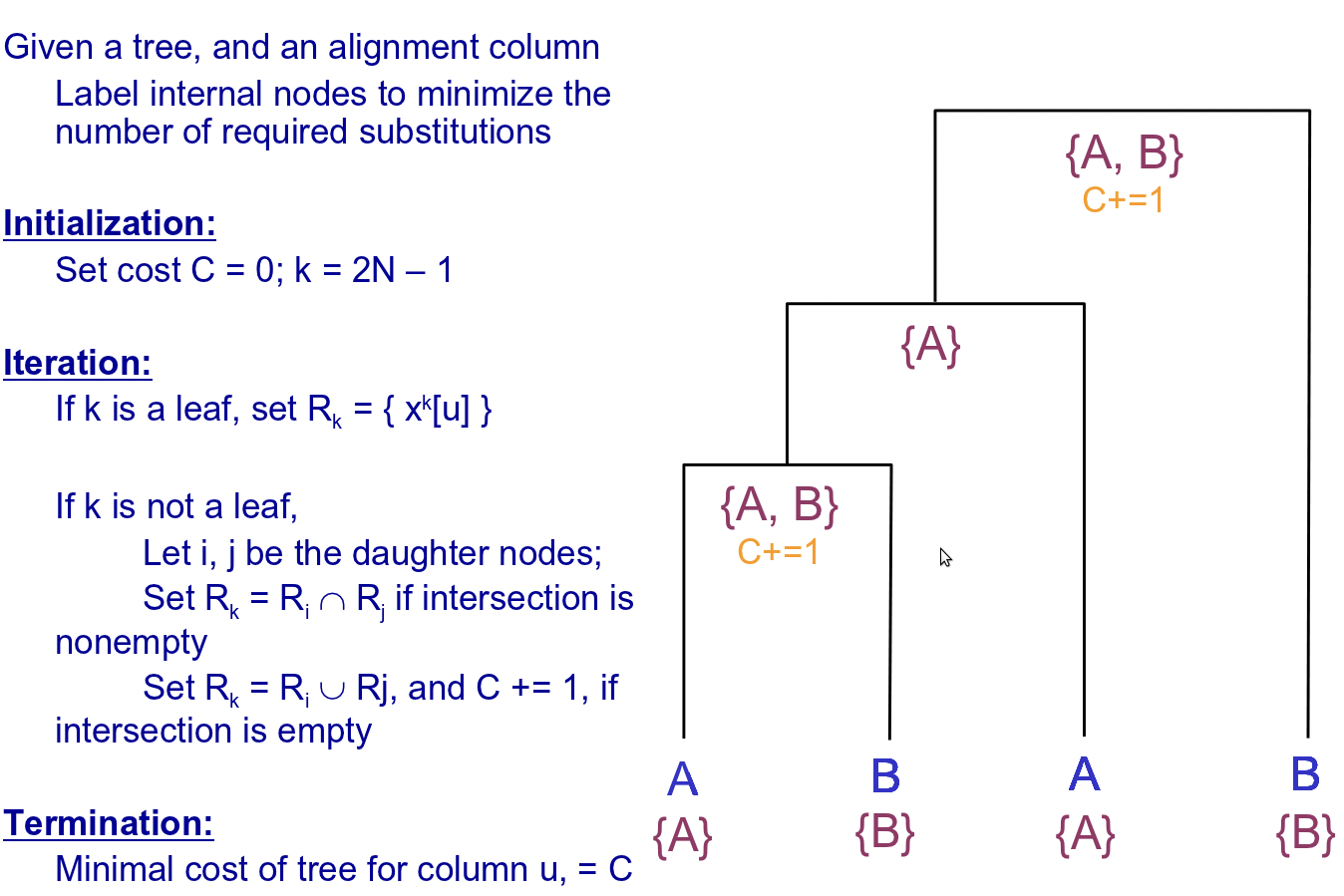
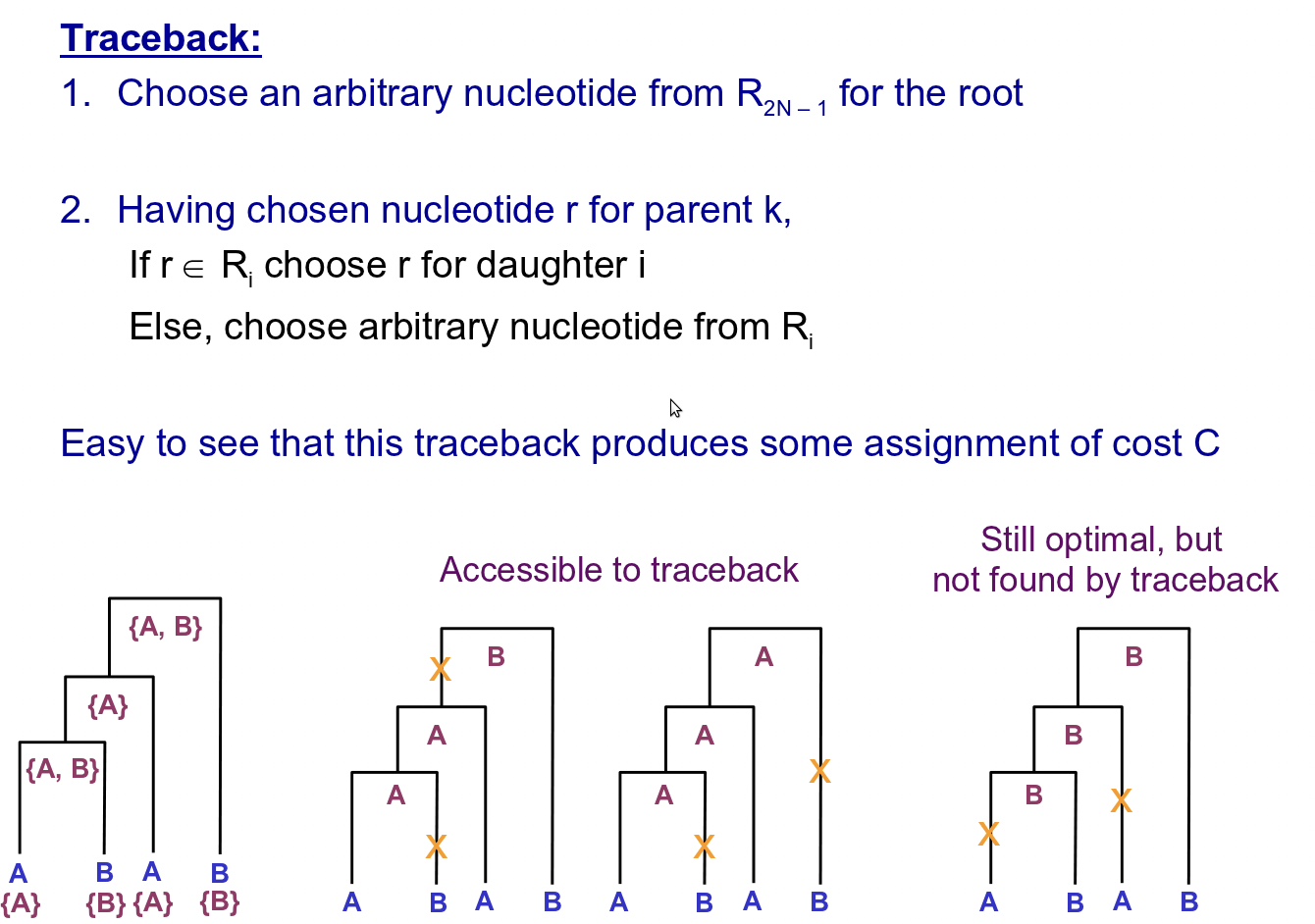
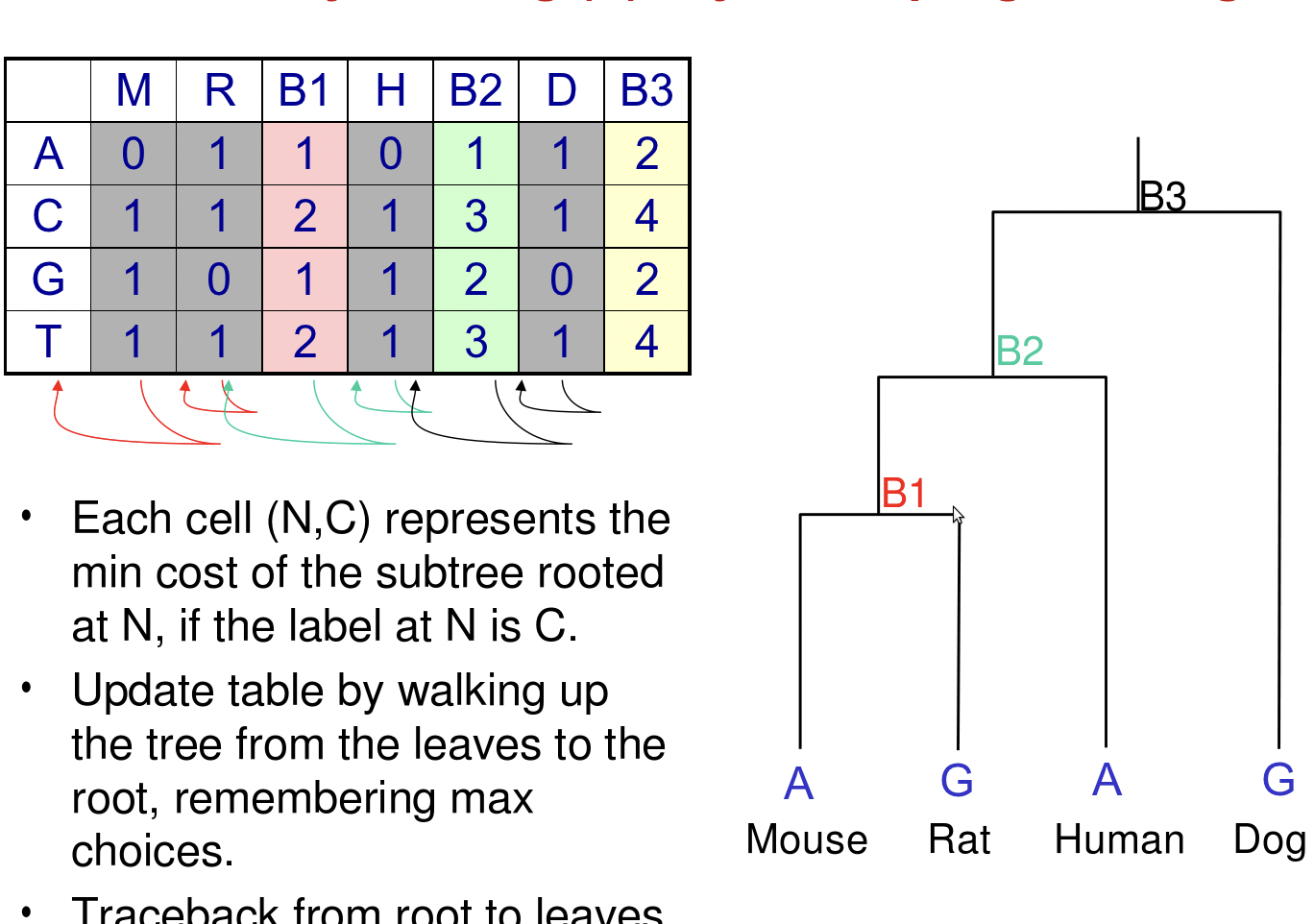
Como mencionamos antes, este método es sencillo y rápido. Sin embargo, esta simplicidad puede distorsionar las puntuaciones que asigna. Por un lado, el algoritmo aquí presentado asume que un par de bases dado se somete a una sustitución a lo largo de como máximo una rama de un nodo dado, lo que puede llevarlo a ignorar muy probablemente secuencias internas que violen esta suposición. Además, este método no modela explícitamente el tiempo representado a lo largo de cada borde y, por lo tanto, no puede explicar la mayor probabilidad de una sustitución a lo largo de bordes que representan una larga duración temporal, o la posibilidad de diferentes tasas de mutación a través del árbol. Los métodos de máxima verosimilitud resuelven ampliamente estas deficiencias y, por lo tanto, se usan más comúnmente para la puntuación

Máxima probabilidad - algoritmo de pelado

Al igual que con los métodos generales de Máxima verosimilitud, este algoritmo puntúa un árbol de acuerdo con la probabilidad conjunta (logarítmica) de observar los datos y el árbol dado, es decir P (D, T). El algoritmo de peeling vuelve a considerar pares de bases individuales y asume que todos los sitios evolucionan de manera independiente. Al igual que en el método de parsimonia, este algoritmo considera todos los pares de bases independientemente: calcula la probabilidad de observar los caracteres dados en cada par base en los nodos hoja, dado el árbol, un conjunto de longitudes de rama, y la asignación de máxima verosimilitud de la secuencia interna, luego simplemente multiplica esta probabilidad sobre todos los pares de bases para obtener la probabilidad total de observar el árbol. Tenga en cuenta que el modelado explícito de longitudes de rama es una diferencia con respecto al enfoque anterior.

Figura 26.18: Un árbol a puntuar usando el algoritmo de peeling. n=4

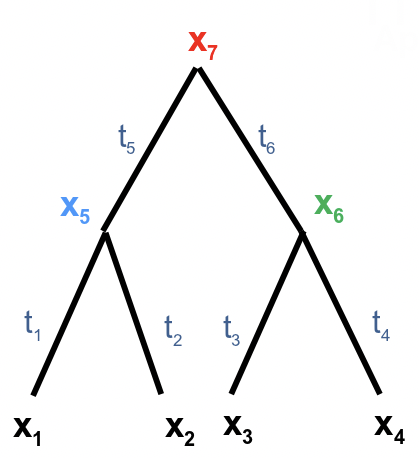
Aquí cada nodo tiene un carácter xi y ti es la longitud de rama correspondiente de su padre. Tenga en cuenta que ya conocemos los valores x ₁, x ₂ ···x _n, por lo que son constantes, pero x _n+1, ···x _2n-1 son caracteres desconocidos en nodos ancestrales que son variables a las que asignaremos valores de máxima verosimilitud. (También tenga en cuenta que hemos adoptado un esquema de indexación de hojas a raíz para los nodos, lo contrario del esquema que usamos antes). Queremos computar P (x ₁ x ₂ · · · x _n |T). Para ello sumamos sobre todas las combinaciones posibles de valores en los nodos ancestrales. A esto se le llama marginación. En este ejemplo particular

\[P\left(x_{1} x_{2} x_{3} x_{4} \mid T\right)=\sum_{x_{5}} \sum_{x_{6}} \sum_{x_{7}} P\left(x_{1} x_{2} \cdots x_{7} \mid T\right)\nonumber\]

Aquí hay 4 términos ^n-1, pero podemos usar el siguiente truco de factorización:

\[=\sum_{x_{7}}\left[P\left(x_{7}\right)\left(\sum_{x_{5}} P\left(x_{5} \mid x_{7}, t_{5}\right) P\left(x_{1} \mid x_{5}, t_{1}\right) P\left(x_{2} \mid x_{5}, t_{2}\right)\right)\left(\sum_{x_{6}} P\left(x_{6} \mid x_{7}, t_{6}\right) P\left(x_{3} \mid x_{6}, t_{3}\right) P\left(x_{4} \mid x_{6}, t_{4}\right)\right)\right] \nonumber\]

Aquí asumimos que cada rama evoluciona de manera independiente. Y la probabilidad P (b|c, t) denota la probabilidad de que la base c mute a la base b dado el tiempo t, que se obtiene esencialmente del modelo Jukes Cantor o algún modelo más avanzado discutido anteriormente. A continuación podemos mover los factores que son independientes de la variable de suma fuera de la suma. Eso da:

\[=\sum_{x_{7}}\left[P\left(x_{7}\right)\left(\sum_{x_{5}} P\left(x_{5} \mid x_{7}, t_{5}\right) P\left(x_{1} \mid x_{5}, t_{1}\right) P\left(x_{2} \mid x_{5}, t_{2}\right)\right)\left(\sum_{x_{6}} P\left(x_{6} \mid x_{7}, t_{6}\right) P\left(x_{3} \mid x_{6}, t_{3}\right) P\left(x_{4} \mid x_{6}, t_{4}\right)\right)\right]\nonumber\]

Sea T _i el subárbol debajo de i. En este caso, nuestro array de programación dinámica 2n-1\(\times\) 4 calcula L [i, b], la probabilidad P (T _i |x _i = b) de observar T _i, si el nodo i contiene base b. Entonces queremos calcular la probabilidad de observar T = T _2n-1 , que es

\[\sum_{b} P\left(x_{2 n-1}=b\right) L[2 n-1, b]\nonumber\]

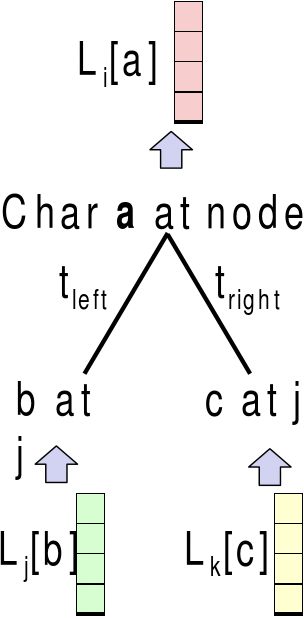
Tenga en cuenta que por cada nodo ancestral i y su hijo j, k, tenemos

\[L[i, b]=\left(\sum_{c} P\left(c \mid b, t_{j}\right) L[j, c]\right)\left(\sum_{c} P\left(c \mid b, t_{k}\right) L[k, c]\right)\nonumber\]

Sujeto a las condiciones iniciales para los nodos hoja, es decir, para i\(\leq\) n:

L [i, b] = 1 si x _i = b y 0 en caso contrario

Figura 27.19: La recurrencia

Tenga en cuenta que todavía no tenemos los valores P (x _2n-1 = b). Por lo general se asigna por igual o de alguna distribución previa, pero no afecta mucho a los resultados. El paso final es, por supuesto, multiplicar todas las probabilidades para sitios individuales para obtener la probabilidad de observar el conjunto de secuencias completas. Además, una vez que hemos asignado los valores de máxima verosimilitud para cada nodo interno dada la estructura de árbol y el conjunto de longitudes de rama, podemos multiplicar la puntuación resultante por algunas probabilidades previas de la estructura de árbol y el conjunto de longitudes de rama, que a menudo se generan utilizando modelos explícitos de procesos evolutivos, como el proceso Yule o modelos de nacimiento-muerte como el proceso Moran. El resultado de esta multiplicación final se denomina probabilidad a posteriori, utilizando el lenguaje de inferencia bayesiana. La complejidad general de este algoritmo es O (nmk ²) donde n es el número de hojas (taxones), m es la longitud de la secuencia y k es el número de caracteres.

Hay addvantages y desventajas de este algoritmo. Tales como

Ventajas:

1. Inherentemente estadístico y basado en modelos evolutivos.
2. Por lo general, el más consistente de los métodos disponibles.
3. Se utiliza tanto para análisis de caracteres como de velocidad
4. Se puede utilizar para inferir las secuencias de los ancestros extintos.

5. Dar cuenta de los efectos de longitud de ramificación en árboles desequilibrados.
6. Secuencias de nucleótidos o aminoácidos, otro tipo de datos.

Desventajas:

1. No tan simples e intuitivos como muchos otros métodos.
2. Intenso computacionalmente Limitado por, número de taxones y longitud de secuencia).

3. Al igual que la parsimonia, puede ser engañada por altos niveles de homoplasía.
4. Las violaciones de los supuestos del modelo pueden dar lugar a árboles incorrectos.

Buscar

Una búsqueda exhaustiva sobre el espacio de todos los árboles sería extremadamente costosa. El número de árboles de enraizamiento completo con n + 1 hojas es el número enésimo catalán

\ [C_ {n} =\ frac {1} {n+1}\ izquierda (\ begin {array} {c}
2 n\\
n
\ end {array}\ derecha)\ approx\ frac {4^ {n}} {n^ {3/2}\ sqrt {\ pi}}\ nonumber\]

Además, debemos calcular el conjunto de verosimilitud máxima de longitudes de rama para cada uno de estos árboles. Por lo tanto, es un problema difícil de NP maximizar la puntuación absolutamente para todos los árboles. Afortunadamente, los algoritmos de búsqueda heurística generalmente pueden identificar buenas soluciones en el espacio del árbol. El marco general para dichos algoritmos de búsqueda es el siguiente:

Inicialización: Tome algún árbol como base de iteración (aleatoriamente o según algún otro anterior, o desde los algoritmos directos basados en la distancia).

Propuesta: Proponer un nuevo árbol modificando ligeramente al azar el árbol actual.

Puntuación: Calificar la nueva propuesta de acuerdo con los métodos descritos anteriormente.

Seleccionar: Seleccione aleatoriamente el nuevo árbol o el árbol viejo (probabilidades correspondientes según la relación de puntuación (verosimilitud).

Iterar: Repita el paso de propuesta a menos que se cumplan algunos criterios de terminación (alguna puntuación umbral o número de pasos alcanzados.

la idea básica aquí es la suposición heurística de que las puntuaciones de árboles estrechamente relacionados son similares, de manera que se pueden obtener buenas soluciones mediante la optimización local sucesiva, que se espera converja hacia una buena solución general.

Propuesta de árbol

Un método para modificar árboles es el Nearest Neighbor Exchange (NNI), ilustrado a continuación.

Figura 27.20: Un paso de unidad usando el esquema de intercambio de vecinos más cercanos

Otro método común, no descrito aquí, es la bisección y unión de árboles (TBJ). El criterio importante para tales reglas de propuesta es que:

1. a) El espacio arbóreo debe estar conectado, es decir, cualquier par de árboles debe ser obtenible entre sí mediante propuestas sucesivas.

2. b) Una nueva propuesta individual debe estar suciamente cercana a la original. Para que sea más probable que sea una buena solución en virtud de la proximidad a una buena solución ya descubierta. Si los pasos individuales son demasiado grandes, el algoritmo puede alejarse de una solución ya descubierta (también depende del paso de selección). En particular, señalar que la medida de similitud por la que la medida de estos tamaños de paso es precisamente la dierencia en las puntuaciones de verosimilitud asignadas a los dos árboles.

Selección

Elegir si adoptar o no una propuesta dada, como el proceso de generar la propuesta misma, es inherentemente heurístico y varía. Una regla general es:

1. Si el nuevo tiene una mejor puntuación, acéptalo siempre.

2. Si tiene peor puntuación, debería haber alguna probabilidad de seleccionarlo, de lo contrario el algoritmo pronto se fijará en unos mínimos locales, ignorando mejores alternativas un poco lejos.

3. No debe haber demasiada probabilidad de seleccionar una nueva propuesta peor, de lo contrario, corre el riesgo de rechazar una buena solución conocida.

Es la compensación entre los pasos 2 y 3 lo que determina una buena regla de selección. Metropolis Hastings es un Método Montecarlo de la Cadena de Markov (MCMC) que define reglas específicas para explorar el espacio estatal de una manera que lo convierte en una muestra de la distribución posterior. Estos algoritmos funcionan algo bien en la práctica, pero no hay garantía para encontrar el árbol apropiado. Entonces se usa un método conocido como bootstrapping, que básicamente es ejecutar el algoritmo una y otra vez usando subconjuntos de los pares base en las secuencias de hoja,. luego favoreciendo árboles globales que coincidan con las topologías generadas usando solo estas subsecuencias.