17.4: Muestreo de Gibbs- Muestra de distribución conjunta (M, Zij)
- Page ID
- 54165
Muestreo de posiciones de motivo basadas en el vector Z
El muestreo de Gibbs es similar al EM excepto que es un proceso estocástico, mientras que EM es determinista. En el paso de expectativa, solo consideramos nucleótidos dentro de la ventana de motivos en el muestreo de Gibbs. En el paso de maximización, tomamos muestras de Z ij y usamos el resultado para actualizar el PWM en lugar de promediar sobre todos los valores como en EM.
Paso 1: Inicialización Al igual que con EM, generas tu PWM inicial con un muestreo aleatorio de posiciones iniciales iniciales. La principal diferencia radica en el paso Maximización. Durante la EM, el algoritmo crea el motivo de secuencia considerando todos los posibles puntos de partida del motivo. Durante Gibbs, el algoritmo escoge un único punto de partida del motivo con la probabilidad de los puntos de partida Z.
Paso 2: Elimina una secuencia, Xi, de tu conjunto de secuencias. Cambiará la ubicación inicial de para esta secuencia en particular.
Paso 3: Actualizar Usando el conjunto restante de secuencias, actualice el PWM contando con qué frecuencia ocurre cada base en cada posición, agregando pseudorecuentos según sea necesario.
Paso 4: Muestra Utilizando el PWM recién actualizado, computar la puntuación de cada punto de partida en la secuencia Xi. Para generar cada puntaje, Zij, se utiliza la siguiente fórmula:
\[ A_{i j}=\frac{\prod_{k=j}^{j+W-1} p_{e k}, k-j+1}{\prod_{k=j}^{j+W-1} p_{c k}, 0} \nonumber \]
Esta es simplemente la probabilidad de que la secuencia se generó usando el motivo PWM dividida por la probabilidad de que la secuencia se generó usando el PWM de fondo.
Seleccione una nueva posición inicial para X i eligiendo aleatoriamente una posición en función de su Z ij.
Paso 5: Iterar Loop de nuevo al Paso 2 e iterar el algoritmo hasta la convergencia.
Más probabilidades de encontrar el máximo global, fácil de implementar
Debido a que Gibbs actualiza su motivo de secuencia durante la Maximización basándose en una sola muestra del Motivo en lugar de cada muestra ponderada por sus puntuaciones, Gibbs es menos dependiente del PWM inicial. Es mucho más probable que EM se atasque en un máximo local que Gibbs debido a este hecho. No obstante, esto no quiere decir que Gibbs siempre devolverá el máximo global. Gibbs debe ejecutarse varias veces para asegurarse de haber encontrado el máximo global y no el máximo local.Dos implementaciones populares de Gibbs Sampling aplicadas a este problema son AlignAce y BioProspector. Un Sampler Gibbs más general se puede encontrar en el programa WinBugs. Tanto AligNace como BioProspector utilizan el algoritmo antes mencionado para varias elecciones de valores iniciales y luego reportan motivos comunes. El muestreo de Gibbs es más fácil de implementar que el E-M, y en teoría, converge rápidamente y es menos probable que se atasque en un óptimo local. Sin embargo, la búsqueda es menos sistemática.
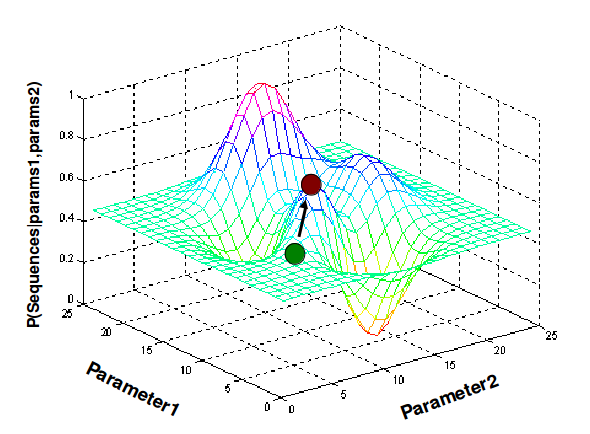
Figura 17.6: Muestreo de Gibbs


