7.1: Patrones de Turing para generar rayas y manchas
- Page ID
- 53119
Alan Turing fue un matemático británico que fue criptógrafo y pionero en informática. Como pasatiempo lateral, también fue un biólogo teórico que desarrolló algoritmos para tratar de explicar patrones complejos utilizando entradas simples y fluctuación aleatoria. Su modelo de "reacción-difusión" utiliza un sistema de dos proteínas para generar un patrón de manchas regularmente espaciadas, que pueden convertirse en franjas con una tercera fuerza externa. En este modelo, hay una proteína activadora que se activa tanto a sí misma como a una proteína inhibidora, que sólo inhibe al activador 1. Por sí misma, la expresión transitoria de la proteína activadora solo produciría un patrón de “ambas proteínas apagadas” o “punto de inhibidor activado” ya que el activador activaría al inhibidor, desactivando así la expresión del activador (Figura 1 caso). Las cosas se ponen más interesantes cuando las moléculas pueden difundirse o transportarse a través del tejido. En este caso, el activador se enciende aleatoriamente y comienza a difundirse alejándose de su fuente puntual, activándose en celdas cercanas. Al mismo tiempo, activa el inhibidor, que también se difunde lejos de la fuente puntual, inhibiendo al activador. Dependiendo del tiempo de activación y difusión o transporte, esto puede resultar en la formación de un anillo expansivo de expresión del activador (Figura 1 tasas iguales). Para obtener manchas, sin embargo, necesitamos dos capas más de complejidad. Primero, debe haber fluctuaciones aleatorias en la expresión que enciendan el activador a niveles bajos a través de un tejido. Segundo, el activador debe difundirse más lentamente que el inhibidor. En este caso, las manchas aleatorias de activador pueden estabilizarse cuando están lo suficientemente alejadas entre sí. Cada una de las pequeñas manchas activa la expresión de activador (que no se difunde rápidamente) e inhibidor (que se difunde demasiado rápido para eliminar completamente la expresión del activador de la fuente puntual inicial). Este gradiente de inhibidor que se difunde desde cada punto evita que las células cercanas produzcan activador. El resultado general de esto es un patrón regular de manchas (Figura 1 paneles inferiores y laterales). El patrón exacto depende del tamaño y la forma del tejido, la velocidad de difusión del activador e inhibidor, así como cualquier otro elemento de patrón que pueda estar presente.
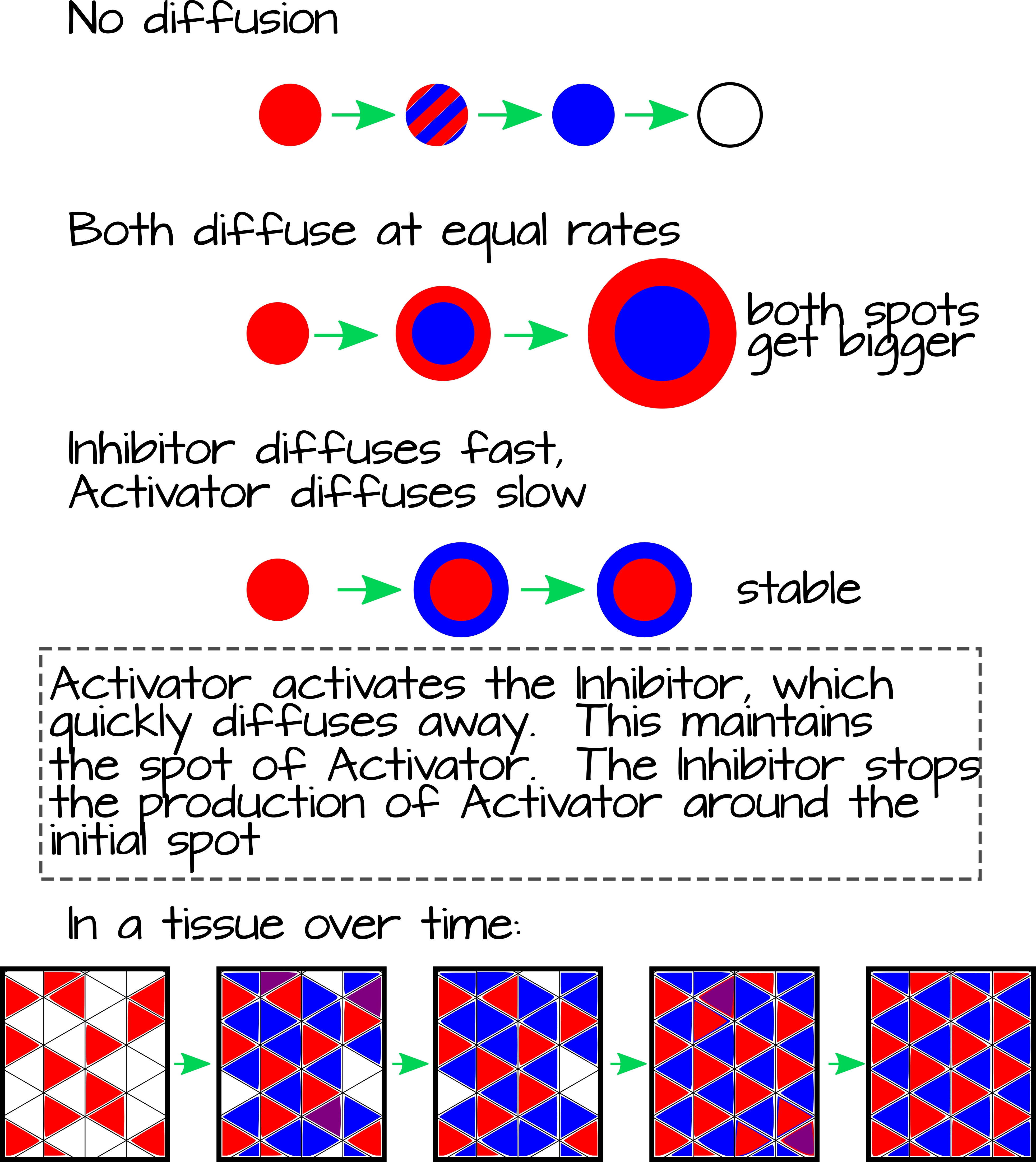
Una versión editable svg de esta figura se puede descargar en: https://scholarlycommons.pacific.edu/open-images/35/
¿Pueden las matemáticas explicar cómo los animales obtienen sus patrones? Cómo el modelo de reacción-difusión de Alan Turing simula patrones en la naturaleza
En un tejido muy largo y estrecho, solo hay una dirección de difusión que puede ocurrir y esto convierte el patrón de puntos de Turing en un patrón de rayas (Figura 2). Fuerzas similares, como el crecimiento direccional y un gradiente morfogénico, también pueden convertir el patrón de puntos en franjas 2. Sin una fuerza externa, el defecto debe ser manchas o un patrón de labrintina serpenteante, dependiendo de las propiedades del activador e inhibidor. Hiscock y Megason proponen cuatro formas principales de obtener un patrón de rayas. Además de hacer que la difusión sea más probable en una dirección que en otra, un tejido puede estar sujeto a un “gradiente de producción”. Este gradiente es una proteína o cofactor transcripcional/traduccional que provoca una mayor expresión génica tanto del activador como del inhibidor en un lado del tejido. Los modelos computacionales predicen que este tipo de gradiente provoca que las franjas se orienten perpendiculares al gradiente (Figura 2) 2. Las rayas se orientarán en paralelo a un “gradiente de parámetros”, donde las propiedades activadoras e inhibidoras de las dos proteínas son mayores en un extremo del tejido que en el otro. Este tipo de modificación podría producirse por un gradiente de una proteína o cofactor que se une al activador y tanto impide que active la expresión génica como sea inhibido por el inihbitor (Figura 2) 2. Finalmente, el tejido puede crecer direccionalmente. Por ejemplo, tus extremidades se desarrollaron en gran medida al crecer lejos de tu cuerpo (distalmente), con una tasa de crecimiento mucho más lenta en otras direcciones. Esto se debe a que la AER en la parte más distal de la yema de la extremidad causa proliferación celular debajo de ella. Un modelo computacional muestra que un modelo de Turing de reacción-difusión generará franjas paralelas a la dirección de crecimiento del tejido (Figura 2) 2. Un minilab nos ayuda a explorar estos modelos más a fondo con una herramienta en línea.
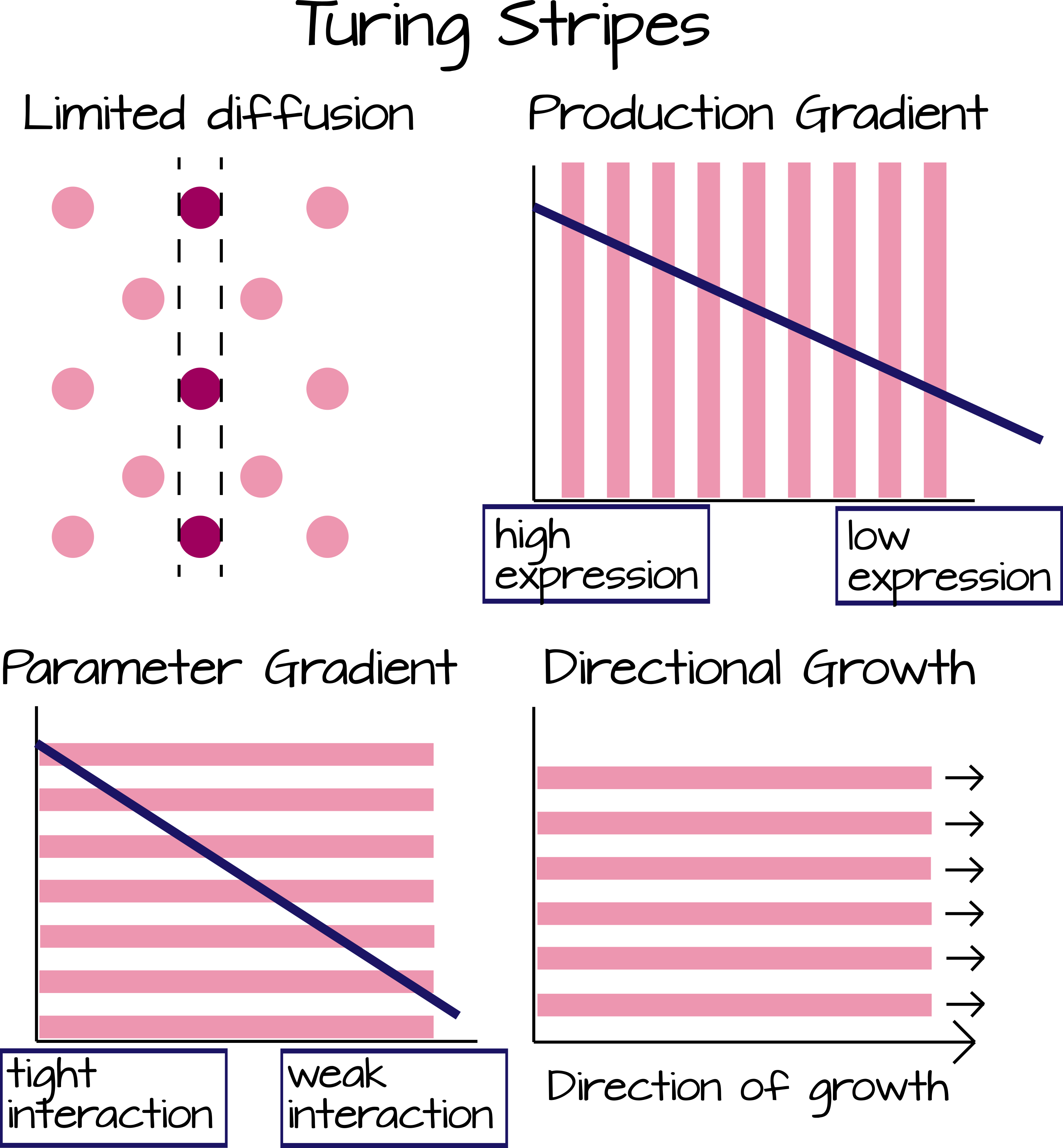
Una versión editable svg de esta figura se puede descargar en: https://scholarlycommons.pacific.edu/open-images/36/


