2.4: Uso de la pendiente topográfica para determinar la altura del árbol
- Page ID
- 52780
Para la mayoría de los fines de manejo de recursos naturales, las áreas terrestres y las distancias se miden en unidades inglesas (Los datos de investigación se recogen en unidades métricas). Por lo tanto, medimos el área en acres, la altura de los árboles en pies y, comúnmente, la distancia horizontal en cadenas (1 cadena = 66 pies). Por esta razón, muchos instrumentos para medir taludes tienen dos escalas:% pendiente y pendiente topográfica. La pendiente topográfica (o Tslope) es esencialmente la misma que% de pendiente, excepto que en lugar de expresar la relación de subida sobre carrera como una proporción de 1:100, Tslope se expresa en una proporción de 1:66 de la siguiente manera:
\[\left(\frac{rise}{run}\right)(66)=\text { Tslope }\]
El multiplicador diferente (66) es la única diferencia entre Tslope y %slope. Para resolver la ecuación de Tslope para “rise” hacemos lo siguiente:
- Multiplique ambos lados de la ecuación por “run” para cancelar la ejecución en el lado izquierdo de la ecuación\[\frac{(r u n)(r i s e)(66)}{r u n}=(run)(\text { Tslope })\]
- Divide ambos lados por “66” para cancelar 66 en el lado izquierdo de la ecuación\[\frac{(\text {rise})(66)}{66}=\frac{(r u n)}{66}(\text { Tslope })\]
Eso nos deja con la siguiente ecuación:
\[rise=\frac{(run)}{66}(\text { Tslope })\]
donde\(rise =height\)
Entonces, al igual que con %slope, el multiplicador Tslope (66) se convierte en el denominador.
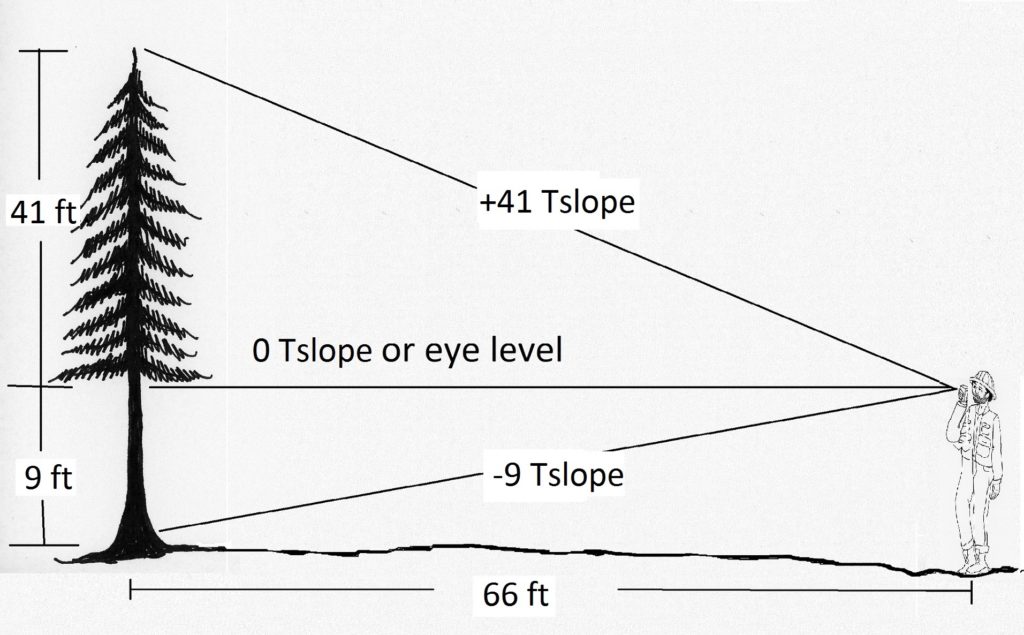
La pendiente topográfica se usa más comúnmente cuando se mide la altura comercial, pero también es fina para medir la altura total en árboles más cortos. Aquí hay un ejemplo (Figura 2.7):
Ejemplo\(\PageIndex{1}\)
Si Jake sale a una distancia horizontal de 66 pies (una cadena) del árbol, su carrera igualará el\(Tslope\) multiplicador. El “66” cancelará, y simplemente puede sumar sus lecturas de pendiente superior y de tocón juntas.
Solución
\[rise=\frac{(run)}{66}\left(T_{\text {slape }}\right)\]
\[rise=\frac{(66)}{66}(41+9)\]
\[\text { rise (height) }=50 \text { feet. }\]


