2.8: Resumen de preguntas

Última actualización
Guardar como PDF

Page ID: 52820

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

1. Determinar las alturas totales de los árboles ilustrados a continuación. Preste atención a las distancias horizontales y la escala de pendiente utilizada para cada una.

2. ¿Cómo se debe determinar la altura total del árbol de la parte superior plana de abajo?

3. Calcula la altura del árbol más magro a continuación.

Respuestas a las preguntas de resumen

1. A.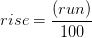 (% pendiente)

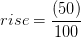(137+11)

subida (altura) = 74 pies

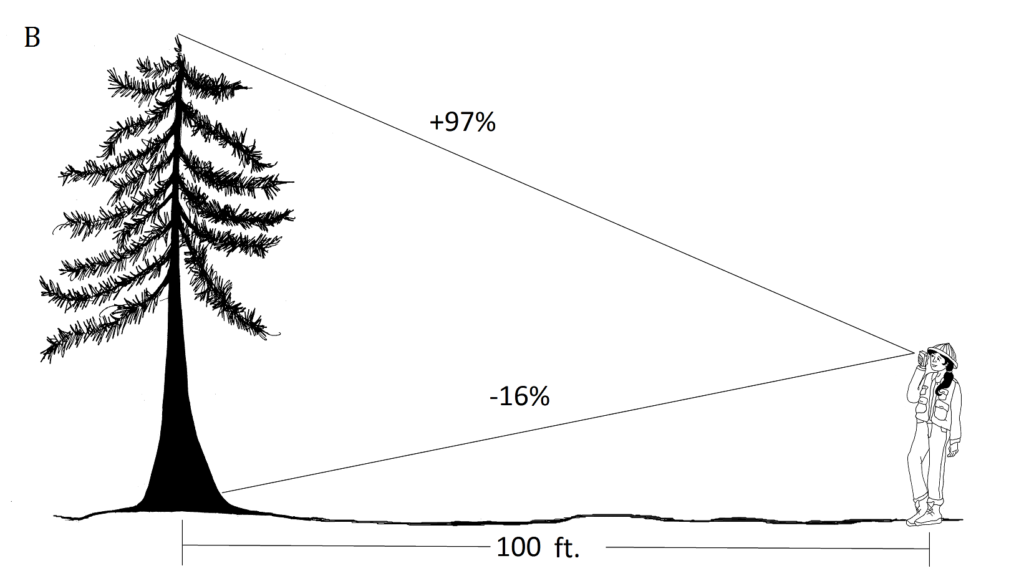
I.B.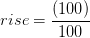 (97+16)

= 113 pies

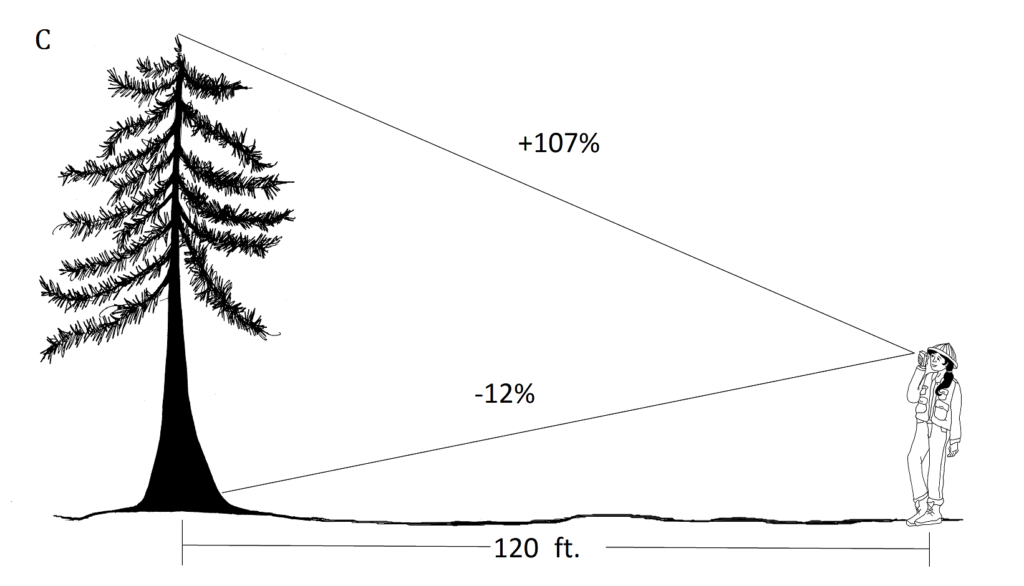
I.C.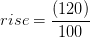 (107+12)

= 143 pies

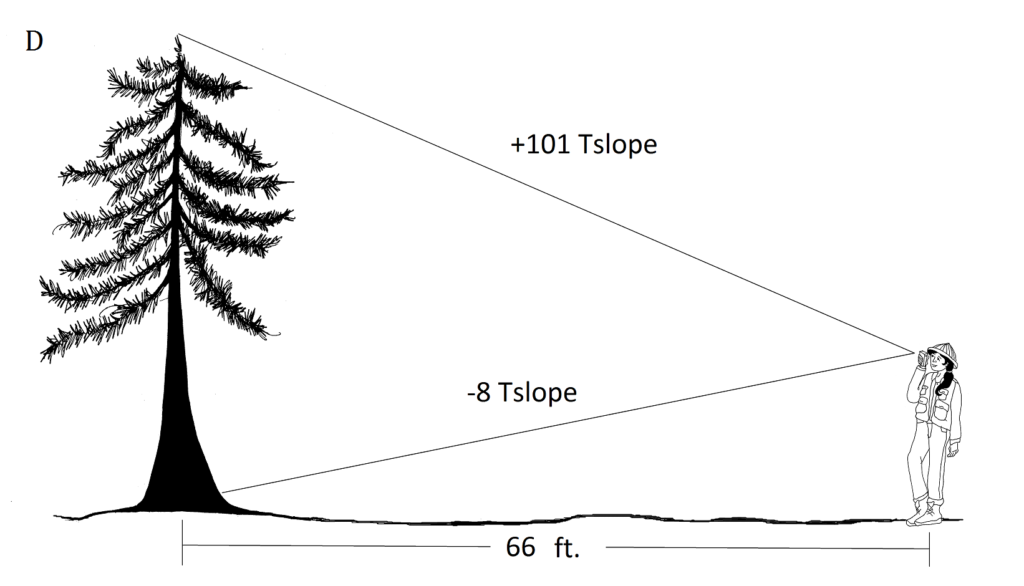
I.D.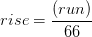 (Tslope)

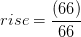(101+8)

subida (altura) = 109 pies

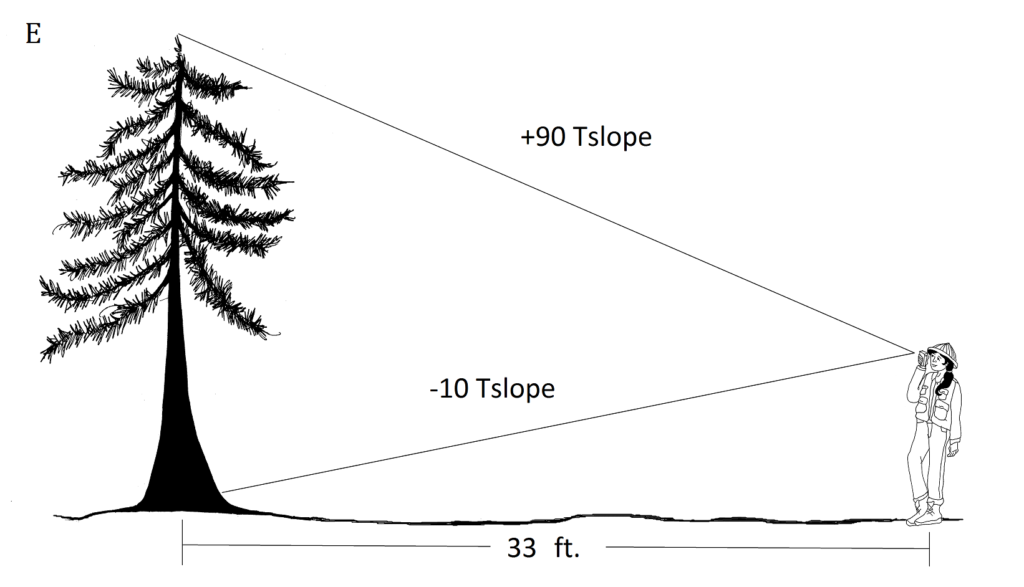
E.I.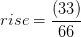 (90+10)

= 50 pies

2. La parte superior del árbol tendrá que ser reconstruida debido a la parte superior rota. Esto se puede hacer usando un árbol vecino que sea similar en tamaño y ahusamiento como referencia.

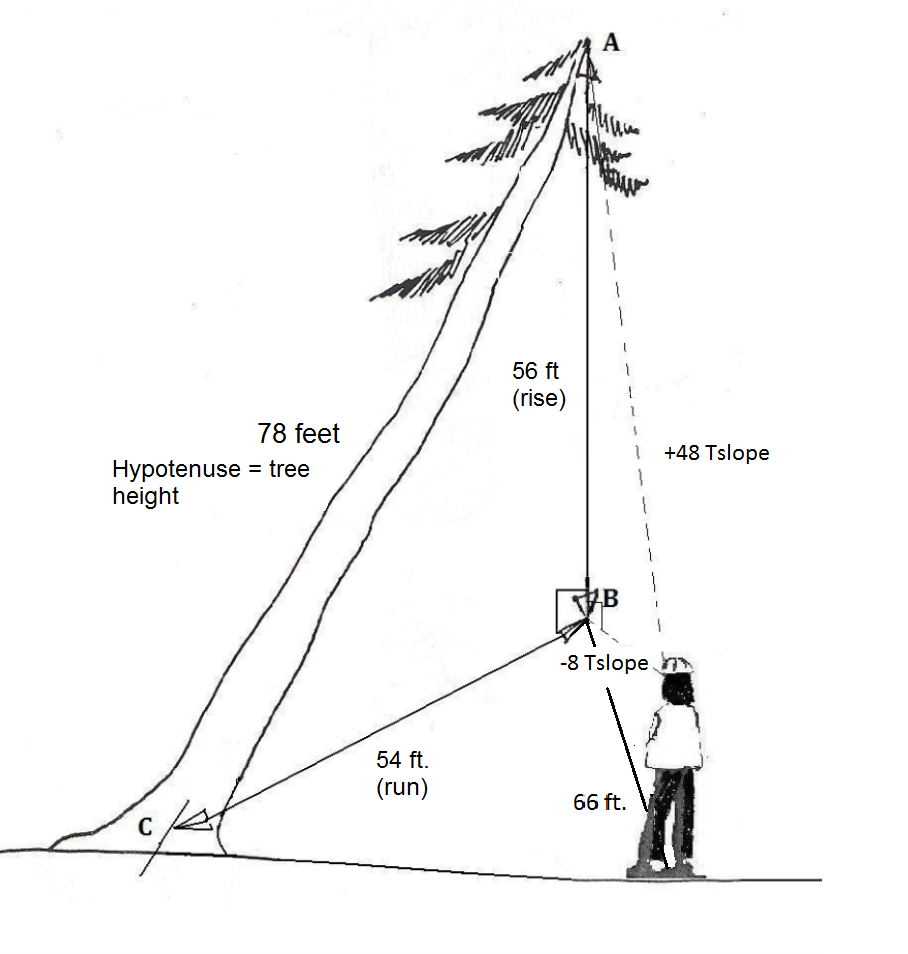
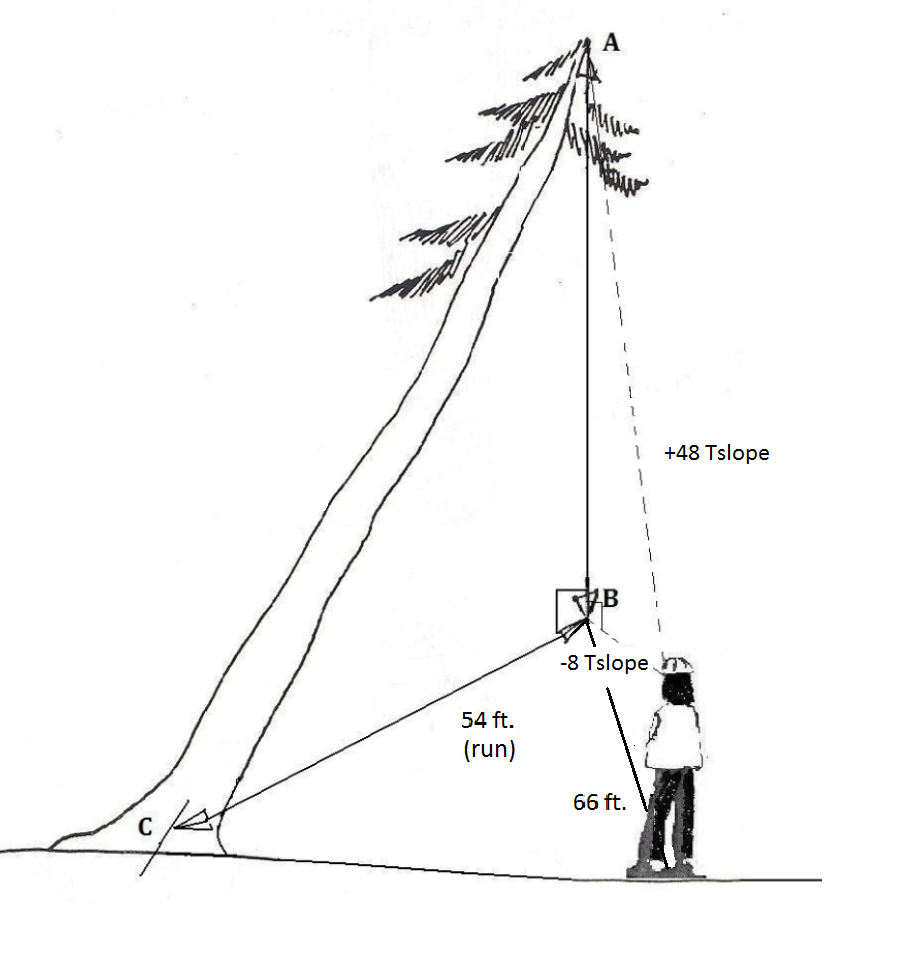
3. a. El ascenso de la línea de caída desde la parte superior del árbol hasta el suelo =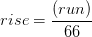 (Tslope)

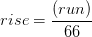(48+8)

= 56 pies

b. La distancia horizontal desde la base del árbol hasta la línea de caída es de 54 pies. Así tenemos dos lados del triángulo rectángulo.

Usando el Teorema de Pitágoras para determinar la longitud del árbol (hipotenusa):

a ² + b ² = c ² donde:

56 ² + 54 ² = c ²

6052 = c ²

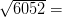78 pies