12: El impacto de la deriva genética en alelos seleccionados
- Page ID
- 58112
“La selección natural es un mecanismo para generar un grado sumamente alto de improbabilidad”. —R.A. Fisher
En el capítulo anterior asumimos que la selección que actuaba sobre nuestros alelos era lo suficientemente fuerte como para que pudiéramos ignorar la acción de la deriva genética en la conformación de frecuencias alélicas. Sin embargo, la deriva genética afecta a todos los alelos, por lo que en este capítulo exploramos la interacción de selección y deriva. Los alelos fuertemente seleccionados pueden perderse de la población a través de la deriva cuando son raros en la población, mientras que los alelos débilmente beneficiosos y débilmente nocivos están sujetos a los caprichos aleatorios de la deriva genética a lo largo de todo su tiempo en la población. Comprender la interacción entre la selección y la deriva genética es clave para comprender hasta qué punto las poblaciones pequeñas pueden estar limitadas por mutación en sus tasas de adaptación, y cómo las tasas de evolución molecular y genómica pueden diferir entre los taxones.
Pérdida estocástica de alelos fuertemente seleccionados
Incluso los alelos fuertemente beneficiosos pueden perderse de la población cuando son suficientemente raros. Esto se debe a que el número de crías que dejan los individuos a la siguiente generación es fundamentalmente estocástico. Un coeficiente de selección de s=\(1\%\) es un coeficiente de selección fuerte, que puede conducir un alelo a través de la población en unos pocos cientos de generaciones una vez establecido el alelo. Sin embargo, si los individuos tienen en promedio un pequeño número de crías por generación, el primer individuo en portar nuestro alelo beneficioso, que tiene en promedio\(1\%\) más hijos que sus compañeros, podría tener fácilmente cero descendencia, lo que lleva a la pérdida de nuestro alelo antes de que tenga la oportunidad de propagación.
Para dar una primera puñalada a este problema, pensemos en una población haploide muy grande en la que un solo individuo comienza con el alelo seleccionado, y preguntemos sobre la probabilidad de pérdida eventual de nuestro alelo seleccionado a partir de esta única copia. Para derivar esta probabilidad de loss (\(p_L\)), haremos uso de un argumento simple. Nuestro alelo seleccionado se perderá eventualmente de la población si cada individuo con el alelo no deja descendientes.
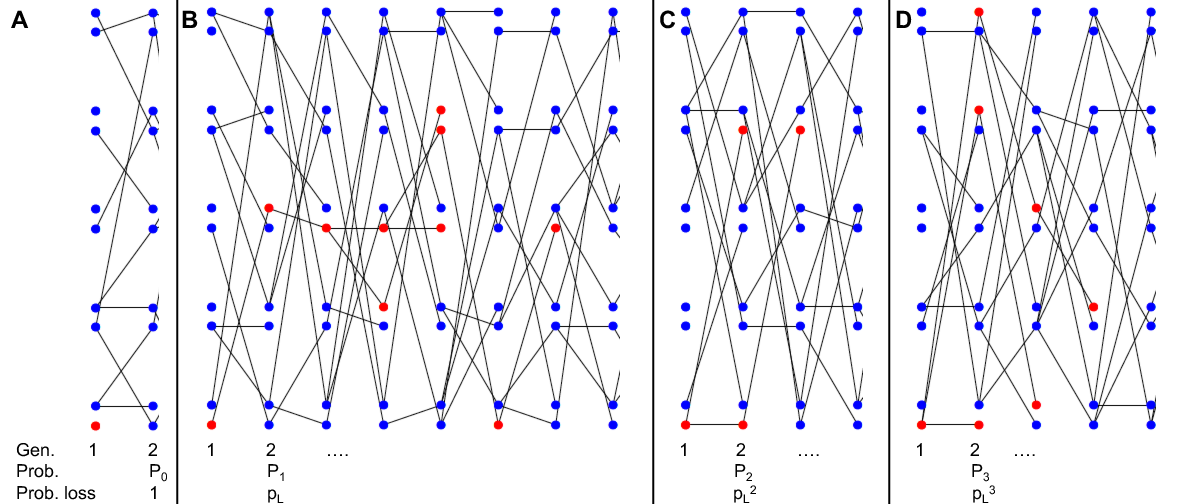
Bueno podemos pensar en diferentes casos:
- En nuestra primera generación, con probabilidad\(P_0\) nuestro alelo individual no deja copias de sí mismo a la siguiente generación, en cuyo caso nuestro alelo se pierde (Figura\(\PageIndex{1}\) A).
- Alternativamente, nuestro alelo podría dejar una copia de sí mismo a la siguiente generación (con probabilidad\(P_1\)), en cuyo caso con probabilidad\(p_L\) esta copia finalmente se extingue (Figura\(\PageIndex{1}\) B).
- Nuestro alelo podría dejar dos copias de sí mismo a la siguiente generación (con probabilidad\(P_2\)), en cuyo caso con probabilidad\(p_L^2\) ambas copias eventualmente se extinguen (Figura\(\PageIndex{1}\) C).
- De manera más general, nuestro alelo podría dejar\(k\) copias (\(k>0\)) de sí mismo a la siguiente generación (con probabilidad\(P_k\)), en cuyo caso con probabilidad\(p_L^k\) todas estas copias eventualmente se extinguen (por ejemplo, Figura\(\PageIndex{1}\) D).
Resumiendo estas probabilidades, vemos que
\[p_L = \sum_{k=0}^{\infty} P_k p_L^{k}\]
Ahora tendremos que especificar\(P_k\), la probabilidad de que un individuo que porta nuestro alelo seleccionado tenga\(k\) descendencia. Para que esta población se mantenga constante en tamaño, asumiremos que los individuos sin la mutación seleccionada tienen en promedio una descendencia por generación, mientras que los individuos con nuestro alelo seleccionado tienen en promedio\(1+s\) descendencia por generación. Supondremos que el número de crías que tiene un individuo es Poisson distribuido con la media dada por\(1\) o\(1+s\), es decir, la probabilidad de que un individuo con el alelo seleccionado tenga\(i\) hijos es
\[P_i= \frac{(1+s)^i e^{-(1+s)}}{i!}\]
Sustituyendo\(P_k\) en la ecuación anterior, vemos
\[\begin{aligned} p_L &= \sum_{k=0}^{\infty} \frac{(1+s)^ke^{-(1+s)}}{k!} p_L^{k} \nonumber \\ &= e^{-(1+s)} \left( \sum_{k=0}^{\infty} \frac{\left(p_L(1+s) \right)^k}{k!} \right)\end{aligned}\]
El término entre paréntesis es en sí mismo una expansión exponencial, por lo que podemos reescribir esta ecuación como
\[p_L = e^{(1+s)(p_L-1)} \label{prob_loss}\]
Resolver para nos\(p_L\) daría nuestra probabilidad de pérdida para cualquier coeficiente de selección. Vamos a reescribir nuestro resultado en términos de la probabilidad de escapar de la pérdida,\(p_F = 1-p_L\). Podemos reescribir la ecuación\ ref {prob_loss} como
\[1-p_F = e^{-p_F(1+s)}\]
\[1-p_F \approx 1-p_F(1+s)+p_F^2(1+s)^2/2\]
Resolviendo esto encontramos que
\[p_F = 2s. \label{eqn:prob_fix_strong}\]
Así, incluso un alelo con coeficiente de\(1\%\) selección tiene una\(98\%\) probabilidad de perderse cuando se introduce por primera vez en la población por mutación.
Si la tasa de mutación hacia nuestro alelo ventajoso es\(\mu\), y hay\(N\) individuos en nuestra población haploide, entonces surgen mutaciones\(N \mu\) ventajosas por generación. Cada una de estas nuevas mutaciones beneficiosas tiene una probabilidad\(p_F\) de fijación. Así es el número de mutaciones ventajosas que surgen por generación que eventualmente se fijarán en la población\(N \mu p_F\), y el tiempo de espera para que surja una mutación que fijará es el recíproco de esto:\(\frac{1}{N\mu p_F}\). Así, al adaptarse a una nueva presión de selección a través de nuevas mutaciones, el tamaño de la población, el tamaño de la diana mutacional y la ventaja selectiva de nuevas mutaciones, todo importa. Una de las razones por las que se utilizan combinaciones de fármacos contra virus como el VIH y la malaria es que, aunque los virus se adapten a uno de los fármacos, la carga viral (\(N\)) del paciente se reduce considerablemente, lo que hace muy poco probable que la población logre fijar un segundo alelo farmacorresistente.
Modelo diploide de pérdida estocástica de alelos fuertemente seleccionados.
También podemos adaptar este resultado a un ajuste diploide. Suponiendo que los heterocigotos para el\(1\) alelo tienen en promedio\(1+hs\) hijos, la probabilidad de que el alelo no\(1\) se pierda, a partir de una sola copia en la población, es
\[p_F = 2 h s \label{eqn:diploid_escape}\]
para\(h>0\). Tenga en cuenta que esta es una parametrización ligeramente diferente de nuestro modelo diploide en el capítulo anterior; aquí\(h\) está el dominio de nuestro alelo positivamente seleccionado, con\(h=1\) correspondiente a la ventaja selectiva total expresada en un individuo con una sola copia. Así, la probabilidad de que no se pierda un alelo beneficioso depende solo de la ventaja relativa de aptitud del heterocigoto; esto se debe a que cuando el alelo es raro suele estar presente en heterocigotos y por lo tanto su probabilidad de escapar de la pérdida solo depende de la aptitud de estos individuos en comparación con homocigotos para el alelo ancestral (suponiendo una población exogámica).
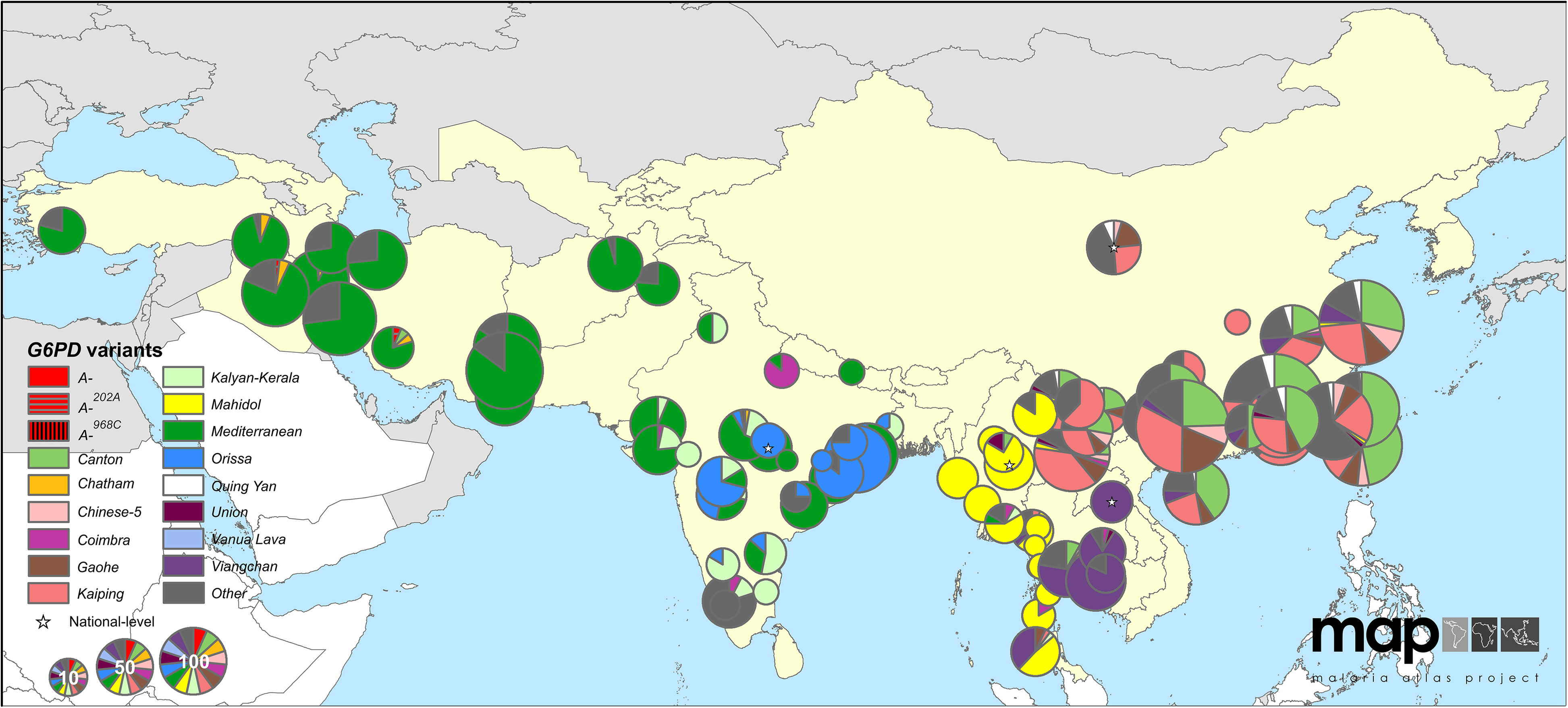
En aproximadamente los últimos diez mil años, los alelos adaptativos que confieren resistencia a la malaria han surgido en varios genes y se han propagado a través de poblaciones humanas en áreas donde la malaria es endémica. Un caso particularmente impresionante de evolución convergente en respuesta a las presiones de selección impuestas por la malaria son los numerosos cambios a lo largo del gen G6PD, que incluyen al menos 15 variantes comunes solo en Asia Central y Oriental que disminuyen la actividad de la enzima. Estos alelos se encuentran ahora con una frecuencia combinada de alrededor del 8% de frecuencia en áreas endémicas de malaria, raramente superando el 20%. Se desconoce si todas estas variantes confieren resistencia a la malaria, pero varios de estos alelos han demostrado efectos contra la malaria y se cree que tienen una ventaja selectiva para los heterocigotos\(sh > 5\%\) donde la malaria es endémica.
Con una ventaja del 5% en heterocigotos, un alelo G6PD presente como una sola copia solo tendría un 10% de probabilidad de fijación en la población. Si es así, ¿cómo es que la adaptación a la malaria ha ocurrido repetidamente a través de cambios en el G6PD? Bueno, tal vez la adaptación no partió de una sola copia del alelo seleccionado. ¿Cuántas copias de los alelos por deficiencia de G6PD esperamos que se estén segregando en la población antes de que cambiaran las presiones de selección?

En ausencia de malaria, estos alelos G6PD son deletéreos con portadores que padecen deficiencia de G6PD, lo que lleva a anemia hemolítica cuando los individuos están expuestos a una variedad de compuestos diferentes, notablemente los presentes en las habas. Hay más de cien bases donde pueden surgir alelos por deficiencia de G6PD, por lo que suponiendo una tasa de mutación\(\approx 10^{-8}\) por par de bases por generación, podemos estimar aproximadamente la tasa de mutaciones que surgen que afectan al gen G6PD\(\mu \approx 10^{-6}\) según generación. En ausencia de malaria, el costo selectivo de ser un heterocigoto portador de un alelo deficiente en G6PD debe haber sido del orden de\(5\%\) o más, y así la frecuencia del alelo bajo equilibrio mutación-selección habría sido\(\approx \frac{10^{-6}}{0.05} =2 \times 10^{-5}\). Asumiendo un tamaño poblacional efectivo de\(2-20\) millones de individuos, hace aproximadamente cinco a diez mil años eso significa que habría habido cuarenta a cuatrocientos ejemplares del alelo por deficiencia de G6PD presentes en la población cuando las presiones de selección cambiaron en la introducción de la malaria. La posibilidad de que uno de estos alelos recién adaptativos se pierda es\(90\%\) pero la posibilidad de que todos estén perdidos es\(<(0.9)^{40}\approx 0.02\), es decir, habría habido una mayor\(98\%\) probabilidad de que la adaptación ocurriera a través de uno o más alelos en G6PD . ¿Cuántos alelos escaparían a la deriva? Bien con\(40 - 400\) copias del alelo pre-malaria, y cada uno de ellos teniendo una\(10\%\) probabilidad de escapar de la deriva, esperamos que entre\(4\) y los alelos\(40\) G6PD escapen a la deriva y contribuyan a la adaptación . Vemos alelos G6PD\(15\) comunes en Eurasia, por lo que nuestro sencillo modelo de adaptación a partir del equilibrio mutación-selección parece razonable.

'El tamiz de Haldane' es el nombre para la idea de que las mutaciones que contribuyen a la adaptación probablemente sean dominantes o al menos codominantes.
- Explique brevemente este argumento con un modelo verbal relativo a los resultados que hemos desarrollado en los dos últimos capítulos.
- Se cree que el tamiz de Haldane es menos importante para la adaptación de la variación de pie previamente perjudicial, que la adaptación de una nueva mutación. ¿Puedes explicar la intuición detrás de esta idea?
- Es probable que el tamiz de Haldane sea menos importante en poblaciones endogámicas, por ejemplo, autofecundantes. ¿Por qué es esto?
La interacción entre la deriva genética y la selección débil
Para alelos fuertemente seleccionados, una vez que el alelo ha escapado a la pérdida inicial a bajas frecuencias, su trayectoria se determinará determinísticamente por sus coeficientes de selección. Sin embargo, si la selección es débil en comparación con la deriva genética, la estocástica de la reproducción puede jugar un papel en la trayectoria que toma un alelo incluso cuando es común en la población. Si la selección es suficientemente débil en comparación con la deriva genética, entonces la deriva genética dominará la dinámica de los alelos y se comportarán como si fueran efectivamente neutrales. Así, la medida en que la selección puede dar forma a los patrones de evolución molecular dependerá de las fuerzas relativas de selección y deriva genética. Pero, ¿qué tan débil debe ser la selección en un alelo para que la deriva domine a la selección? ¿Y estas interacciones entre la selección y la deriva tienen consecuencias a largo plazo para la evolución de los patrones de todo el genoma?
Para modelar la selección y derivar cada generación, primero podemos calcular el cambio determinista en nuestra frecuencia alélica debido a la selección usando nuestra fórmula determinista. Luego, usando nuestra frecuencia de alelos esperada recién calculada, podemos muestrear binomialmente dos alelos para cada una de nuestras crías para construir la siguiente generación. Este enfoque para modelar conjuntamente la deriva genética y la selección se llama el modelo Wright-Fisher.
Bajo el modelo Wright-Fisher, calcularemos el cambio esperado en la frecuencia alélica debido a la selección y la varianza alrededor de esta expectativa por deriva. Para hacer nuestros cálculos más sencillos, supongamos un modelo aditivo, es decir\(h=1/2\), y\(s \ll 1\) eso para que\(\overline{w} \approx 1\). Usando nuestro modelo determinista de selección direccional, del Capítulo\ ref {Chapter:OneLocusSelection}, y estas aproximaciones nos dan nuestro cambio determinista debido a la selección
\[\Delta_S p = \mathbb{E}(\Delta p) = \frac{s}{2} p(1-p) \label{eqn:WF_mean}\]
Para obtener nuestra nueva frecuencia en la próxima generación,\(p_1\), realizamos muestras binomiales de nuestra nueva frecuencia determinista\(p^{\prime}= p + \Delta_S p\), por lo que la varianza en nuestro cambio de frecuencia alélica de una generación a la siguiente viene dada por
\[Var(\Delta p) = Var(p_1 - p) = Var(p_1) = \frac{p^{\prime}(1-p^{\prime})}{2N} \approx \frac{p(1-p)}{2N}. \label{eqn:WF_var}\]
donde la frecuencia alélica anterior\(p\) cae porque es una constante y la varianza en nuestra nueva frecuencia alélica se deriva del hecho de que estamos muestreando binomialmente\(2N\) nuevos alelos de una frecuencia\(p^{\prime}\) para formar la siguiente generación.
Para obtener nuestro primer vistazo a los efectos relativos de la selección vs. deriva, simplemente podemos observar cuándo nuestro cambio en la frecuencia de los alelos causado por la selección dentro de una generación se transmite razonablemente fielmente a través de las generaciones. En particular, si nuestro cambio esperado en la frecuencia alélica es mucho mayor que la varianza alrededor de este cambio, la deriva genética jugará poco papel en el destino de nuestro alelo seleccionado (una vez que el alelo no esté en un número de copias bajo dentro de la población). ¿Cuándo deriva genética dominante la selección? Esto sucederá si\(\mathbb{E}(\Delta p) \gg Var(\Delta p)\), es decir, cuándo\(|Ns| \gg 1\). Por el contrario, cualquier esperanza de nuestro alelo seleccionado siguiendo su camino determinista se deshará rápidamente si nuestro cambio en las frecuencias alélicas debido a la selección es mucho menor que la varianza inducida por la deriva. Entonces, si el valor absoluto de nuestro coeficiente de selección población-tamaño-escala\(| Ns| \ll 1\), entonces la deriva dominará el destino de nuestro alelo.
Para avanzar más en la comprensión del destino de los alelos con coeficientes de selección del orden se\(\frac{1}{N}\) requiere un modelado más cuidadoso. Sin embargo, bajo nuestro modelo diploide, con un coeficiente de selección aditiva\(s\), podemos obtener la probabilidad de que el alelo se\(1\) fije dentro de la población, a partir de una frecuencia\(p\):
\[p_F(p) = \frac{1-e^{-2Ns p }}{1-e^{-2Ns}} \label{eqn:prob_fixed}\]
A continuación se esboza la prueba de este resultado (ver Sección 1.1). Un nuevo alelo que llega a la población con frecuencia\(p=1/(2N)\) tiene una probabilidad de alcanzar la fijación de
\[p_F \left(\frac{1}{2N} \right) = \frac{1-e^{-s }}{1-e^{-2Ns}} \label{eqn:new_mut_prob_fixed}\]
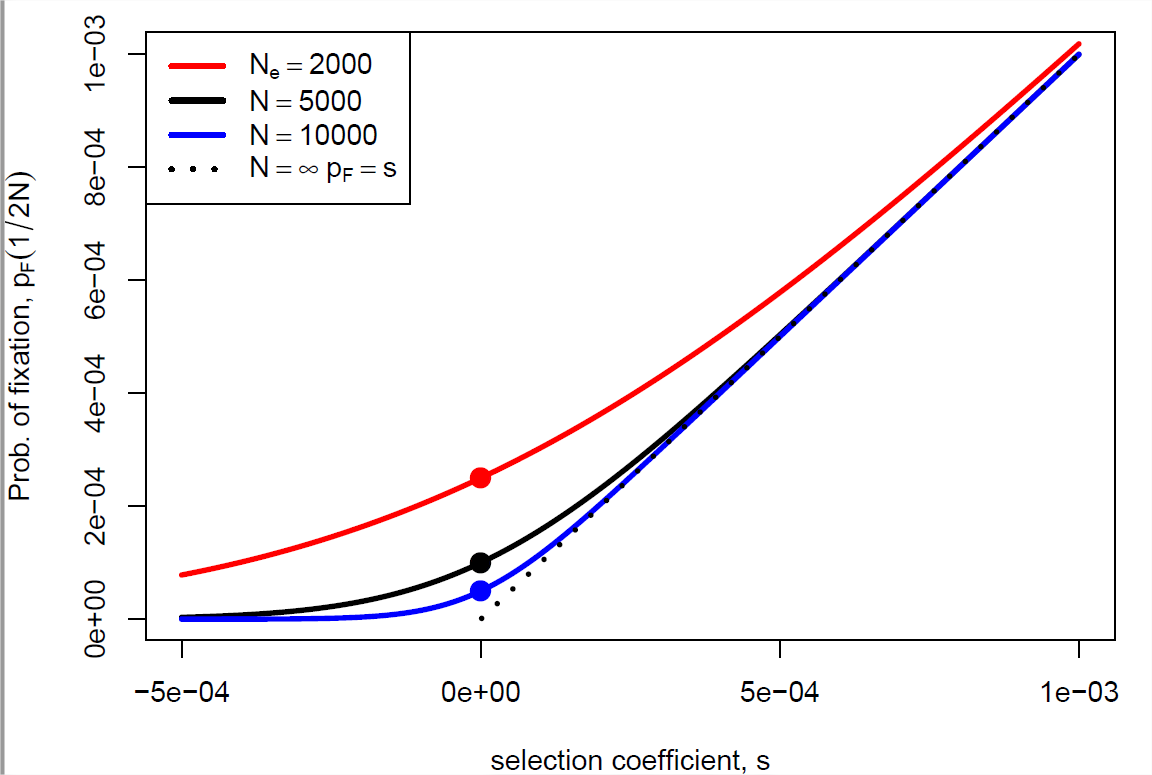
Si\(s \ll1\) pero\(Ns \gg 1\) entonces\(p_F(\frac{1}{2N}) \approx s\), lo que amablemente nos devuelve el resultado que obtuvimos anteriormente para un alelo bajo selección fuerte (Ecuación\ ref {eqn:diploid_escape}). Nuestra probabilidad de fijación (Ecuación\ ref {eqn:new_mut_prob_fixed}) se traza como una función de\(s\) y\(N\) en la Figura\(\PageIndex{7}\). Para recuperar nuestro resultado neutral, podemos tomar el límite\(s \rightarrow 0\) para obtener nuestra probabilidad de fijación neutra,\(\frac{1}{2N}\).
En el caso de\(Ns\) que esté cerca de\(1\), entonces
\[p_F \left( \frac{1}{2N} \right) \approx \frac{s}{1-e^{-2Ns}} \label{eqn:escape_from_intro}\]
Esto es mayor que nuestro resultado anterior del argumento\(p_F=s\) del proceso de ramificación (usando nuestro modelo aditivo de\(h=1/2\)), cada vez más para los más pequeños\(N\). ¿Por qué es esto? Bueno, en una población más pequeña una nueva mutación comienza con una frecuencia mayor (\(\frac{1}{2N}\)) que en una población mayor, esto da un impulso inicial al alelo seleccionado en poblaciones más pequeñas.
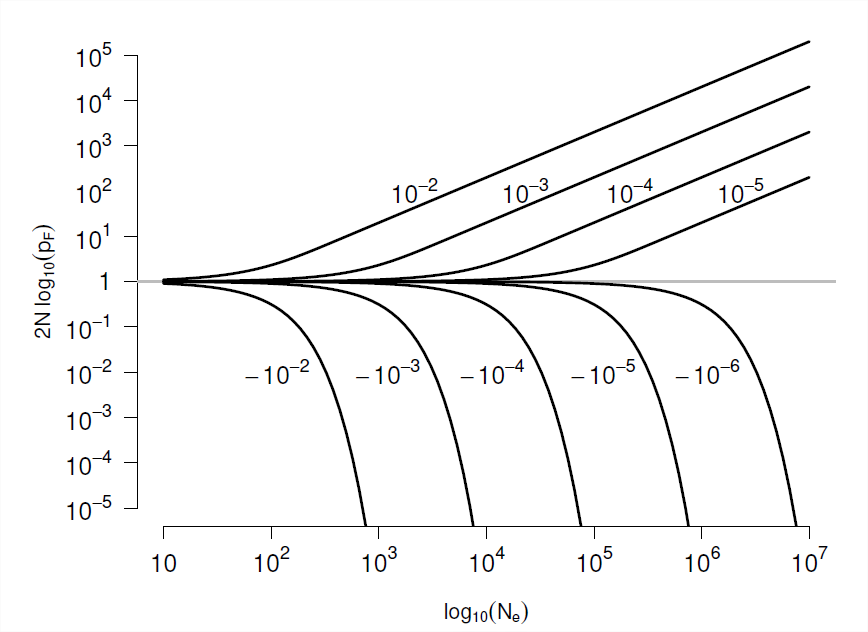
Si, para que la selección opere sobre un alelo, necesitamos que el coeficiente de selección satisfaga\(|Ns|\gg 1\), entonces eso sostiene si\(|s|\gg \frac{1}{N}\). Bueno, los tamaños efectivos de la población suelen ser razonablemente grandes, del orden de cientos de miles o millones de individuos, por lo que los coeficientes de selección del orden de\(10^{-5}\) a\(10^{-6}\) pueden seleccionarse efectivamente sobre, estos representan (des) ventajas increíblemente leves en términos del número de crías que dejan a la siguiente generación (ver Figura\(\PageIndex{8}\)). Si bien somos incapaces de detectar midiendo todos los tamaños excepto los grandes efectos de aptitud física, excepto en algunos experimentos elegantes (por ejemplo, en microbios), tales efectos pequeños son visibles para la selección en grandes poblaciones. Por lo tanto, si se ejercen presiones de selección consistentes durante largos períodos de tiempo, la selección natural puede afinar potencialmente varios aspectos de un organismo.
Como ejemplo de esta afinación, considere cuán cuidadosamente elaborada y optimizada es la secuencia de codones para la traducción. Debido a la degeneración del código proteico, múltiples codones codifican para el mismo aminoácido. Por ejemplo, hay seis codones diferentes que pueden codificar leucina. Si bien estos codones sinónimos son equivalentes a nivel de proteína, las células sí difieren en el número de moléculas de ARNt que se unen a estos codones y por lo tanto la eficacia y precisión con la que se pueden formar proteínas a través de la traducción y el plegamiento. Estas ligeras diferencias en las tasas de traducción probablemente a menudo corresponden a pequeñas diferencias en la condición física, pero ¿importan?
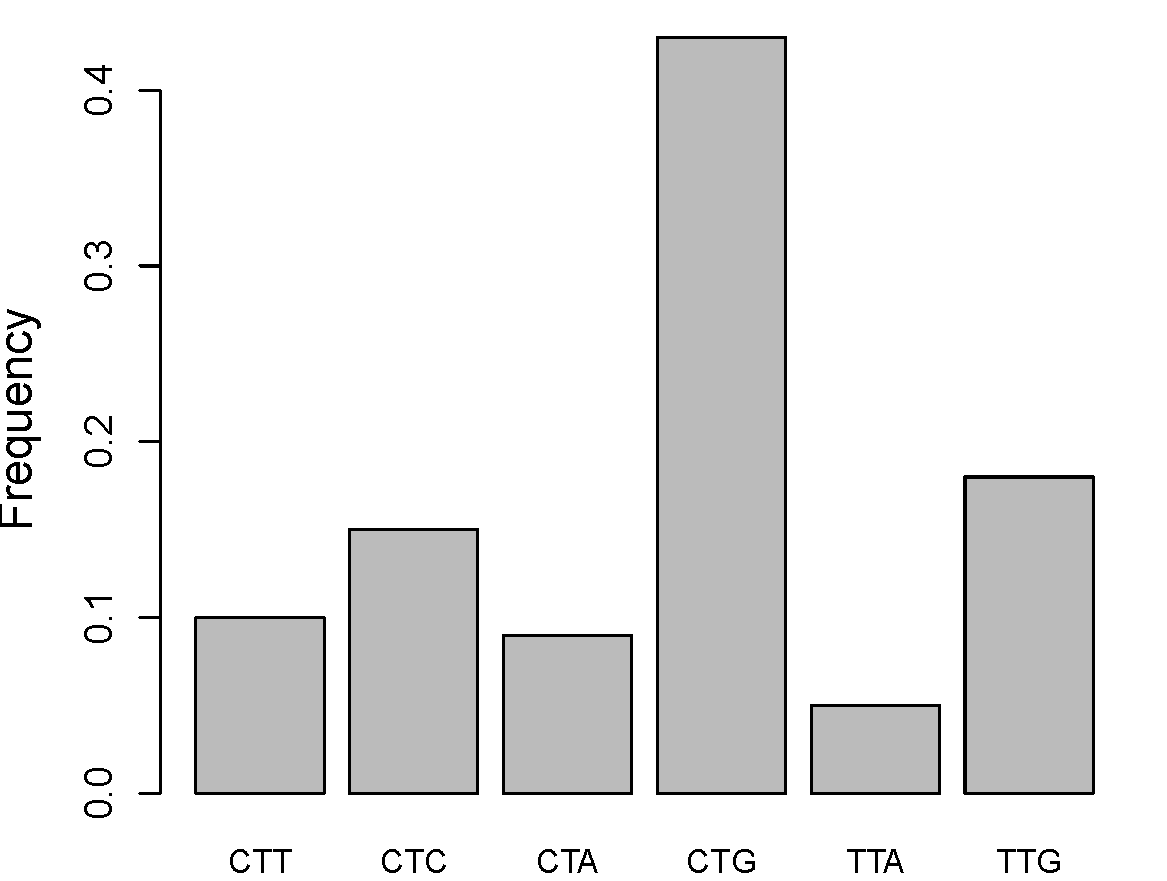
En muchos organismos existe un fuerte sesgo en los codones para codificar aminoácidos particulares, ver Figura\ ref {fig:leucina}, con el codón más abundante que coincide con el ARNt más abundante en las células. Este “sesgo de codón” probablemente refleja la acción combinada de selección débil y presión mutacional, empujando la composición de codones del genoma y las abundancias de ARNt hacia un compromiso adaptativo. Estas presiones de selección han actuado durante largos períodos de tiempo, ya que los patrones de uso de codones suelen ser muy similares para especies que divergieron hace muchas decenas de millones de años. En comparación con otros genes, los genes altamente expresados muestran un fuerte sesgo hacia el uso de codones que coinciden con los ARNt abundantes, consistente con la idea de que el contenido de codones sinónimos de genes altamente expresados está evolucionando para optimizar su traducción (ver Figura\ ref {fig:gene_expression_codon_bias} para un ejemplo temprano). Estos patrones probablemente representan la acción de presiones de selección que son increíblemente débiles en promedio, pero que se han desarrollado a lo largo de vastos períodos de tiempo.
La fijación de alelos ligeramente deletéreos
De la Figura\(\PageIndex{7}\) podemos ver que los alelos débilmente deletéreos también se pueden fijar, especialmente en poblaciones pequeñas. Para entender cuán probable es que los alelos deletéreos por casualidad alcancen la fijación por deriva genética, supongamos un modelo diploide con selección aditiva (con un coeficiente de selección de\(-s\) contra nuestro alelo\(2\)).
Si\(N s \gg 1\) entonces nuestro alelo deletéreo (alelo\(2\)) no puede llegar a la fijación. Sin embargo, si no\(Ns\) es grande, entonces la probabilidad de fijación
\[p_F \left( \frac{1}{2N} \right) \approx \frac{s}{e^{2Ns}-1} \label{eqn:fix_deleterious}\]
para nuestro alelo deletéreo de una sola copia. Así que los alelos deletéreos pueden fijarse dentro de las poblaciones (aunque a una tasa baja) si no\(Ns\) es demasiado grande. Como antes, esto se debe a que si bien las mutaciones deletéreas nunca escaparán a la pérdida en poblaciones infinitas, pueden llegar a fijarse en población finita al alcanzar\(2N\) copias.
Surge una mutación aditiva que disminuye la aptitud relativa de los heterocigotos por\(10^{-5}\). ¿Cuál es la probabilidad de que esta mutación se fije en una población diploide con tamaño efectivo de\(10^4\)? ¿Cuál es la probabilidad que fija en una población de tamaño efectivo\(10^6\)? Al comparar ambos con su probabilidad neutra describir la intuición detrás de este resultado.
OHTA propuso la teoría 'casi neutra' de la evolución molecular en una serie de artículos. Ella sugirió que una fracción razonable de mutaciones funcionales recién nacidas puede tener coeficientes de selección muy débiles, de manera que las especies con tamaños de población efectivos más pequeños pueden tener mayores tasas de fijación de estos alelos muy débilmente perjudiciales. En efecto, su sugerencia es que el parámetro\(C\) de restricción de una región funcional no es una propiedad fija, sino que depende de la capacidad de la población para resistir la afluencia de mutaciones muy débilmente deletéreas.
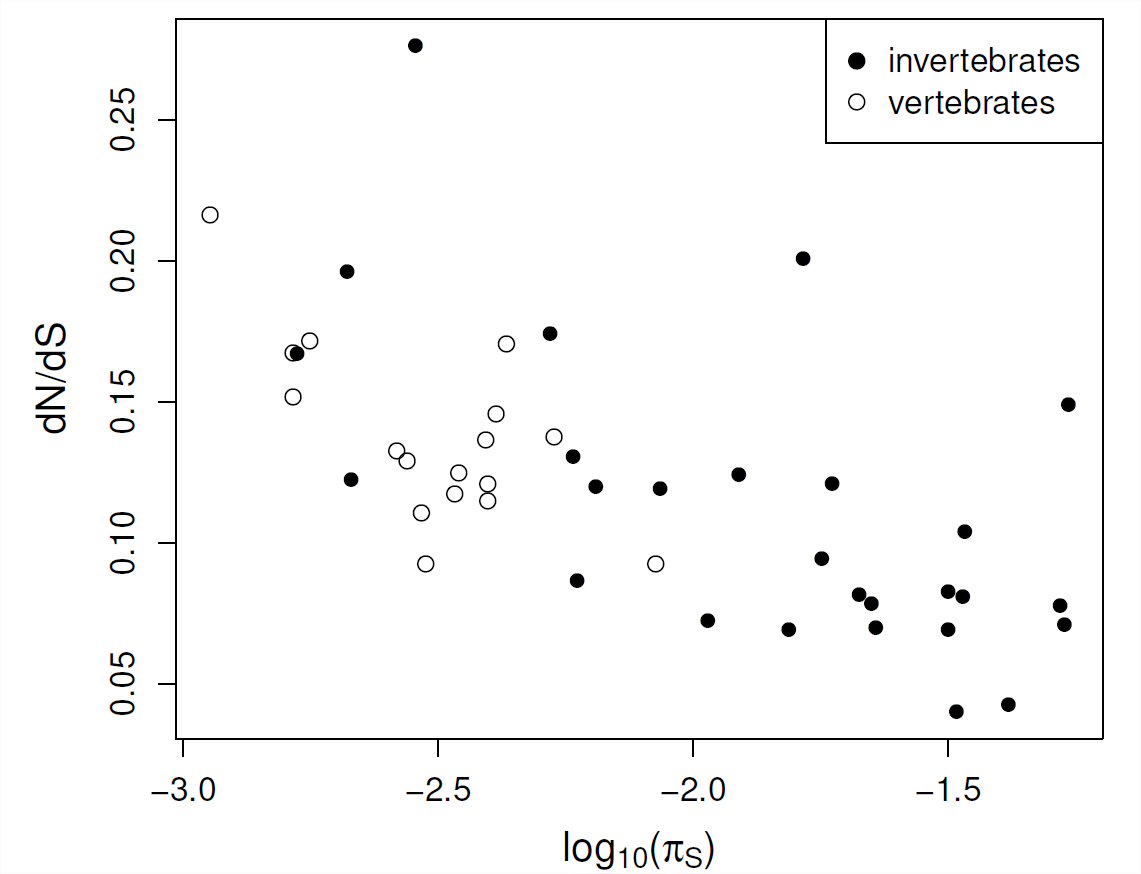
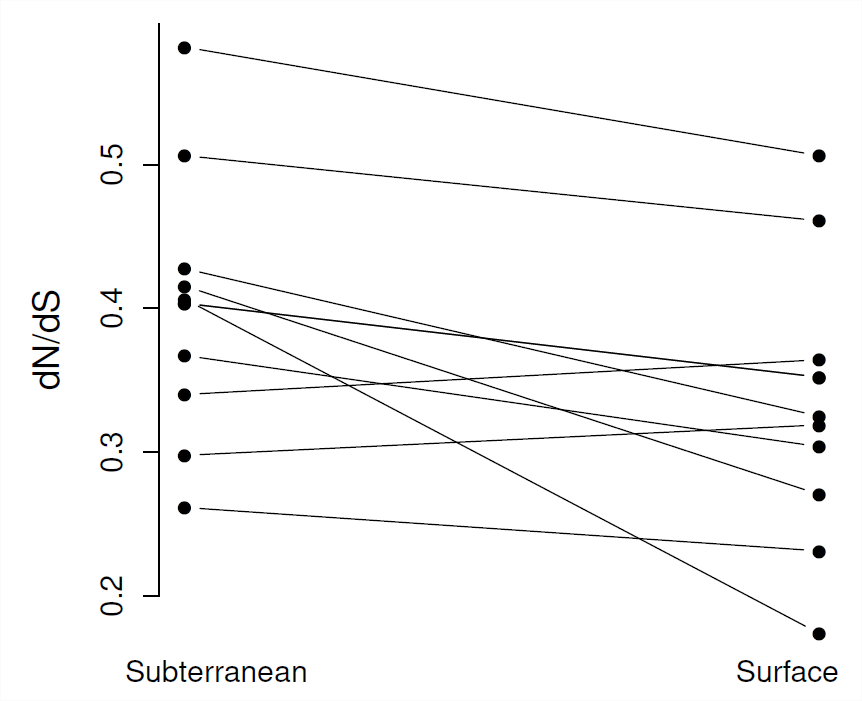
En todas las especies, los promedios de todo el genoma\(\frac{d_N}{d_S}\) parecen estar correlacionados con medidas del tamaño efectivo de la población (como la diversidad sinónima), ver Figura\(\PageIndex{9}\). Esta evidencia apoya la idea de que en especies con tamaños de población efectivos más pequeños (menores\(\pi_S\)), las proteínas pueden estar sujetas a menores grados de restricción, ya que mutaciones muy débilmente perjudiciales son capaces de fijar. Por lo tanto, alguna proporción razonable de sustituciones funcionales en poblaciones con tamaños de población efectivos pequeños, como los humanos, puede ser levemente perjudicial.
Apéndice: La probabilidad de fijación de alelos débilmente seleccionados
¿Cuál es la probabilidad de que un alelo aditivo débilmente beneficioso o deletéreo fije en nuestra población? Dejaremos\(P(\Delta p)\) ser la probabilidad de que nuestra frecuencia alélica cambie\(\Delta p\) en la próxima generación. Usando esto, y siguiendo el argumento de difusión de, podemos escribir nuestra probabilidad de fijación\(p_F(p)\) en términos de la probabilidad de lograr una fijación promediada sobre la frecuencia en la próxima generación
\[p_F(p) = \int p_F(p+\Delta p) P(\Delta p) d(\Delta p) \label{eqn:prob_fix_diff_step1}\]
Esto es muy similar a la técnica que utilizamos al derivar nuestra probabilidad de escapar de la pérdida en una población muy grande arriba.
Entonces necesitamos una expresión para\(p_F(p+\Delta p)\). Para obtener esto, haremos una expansión de la serie Taylor de\(p_F(p)\), asumiendo que\(\Delta p\) es pequeña:
\[p_F(p+\Delta p) \approx p_F(p) + \Delta p \frac{dp_F(p)}{dp} + (\Delta p)^2 \frac{d^2p_F(p)}{dp^2} (p)\]
haciendo caso omiso de términos de orden superior.
Tomando la expectativa\(\Delta p\) en ambos lados, como en la Ecuación\ ref {eqn:prob_fix_diff_step1}, obtenemos
\[p_F(p) = p_F(p) + \mathbb{E}(\Delta p) \frac{dp_F (p)}{dp} + \mathbb{E}((\Delta p)^2) \frac{d^2p_F(p)}{dp^2}\]
Bueno,\(\mathbb{E}(\Delta p) = \frac{s}{2}p(1-p)\) y\(Var(\Delta p)= \mathbb{E}((\Delta p)^2)-\E^2(\Delta p)\), entonces si\(s \ll 1\) entonces\(\E^2(\Delta p) \approx 0\), y\(\mathbb{E}(\Delta p)^2 = \frac{p(1-p)}{2N}\). Sustituyendo en estos valores y restando\(p\) de ambos lados de nuestra ecuación, esto nos deja con
\[0= \frac{s}{2}p(1-p)\frac{dp_F (p) }{dp} + \frac{p(1-p)}{2N} \frac{d^2p_F (p) }{dp^2}\]
y podemos especificar las condiciones de contorno a ser\(p_F(1)=1\) y\(p_F(0)=0\). Resolver esta ecuación diferencial es un proceso algo complicado, pero al hacerlo encontramos que
\[p_F(p) = \frac{1-e^{-2Ns p }}{1-e^{-2Ns}}\]
Esta prueba puede extenderse a alelos con dominio arbitrario, sin embargo, esto no conduce a una expresión analíticamente tratable por lo que no perseguimos esto aquí.
Resumen del capítulo 12
- Incluso los alelos fuertemente ventajosos pueden perderse cuando son raros en la población. En una población haploide es la probabilidad de que un alelo fuertemente aventajoso escapa a la pérdida a partir de una sola copia\(p_F=2s\). En una población diploide esta probabilidad es\(p_F=2hs\), donde\(hs\) está la ventaja relativa de aptitud para heterocigotos. Los alelos fuertemente deletéreos no se pueden fijar en grandes poblaciones.
- Los alelos se seleccionan fuertemente cuando su coeficiente de selección absoluto a escala poblacional es\(|Ns| \gg 1\). Los alelos son efectivamente neutrales cuando\(|Ns| \ll 1\). Alelos que se seleccionan débilmente cuando su\(|Ns|\) está en orden\(1\).
- Las dinámicas de los alelos débilmente seleccionados están sujetas a selección y deriva genética a lo largo de su tiempo en la población, y su probabilidad de fijación (\(p_F\)) depende de\(N\) y\(s\).
- Los alelos muy débilmente seleccionados se pueden seleccionar de manera eficiente en grandes poblaciones. Así, los niveles de restricción evolutiva pueden ser más fuertes en especies con grandes tamaños de población a largo plazo.
Las ardillas melánicas sufren una mayor tasa de depredación (debido a los halcones) que las ardillas normalmente pigmentadas grises. El melanismo se debe a una mutación autosómica dominante. La frecuencia de las ardillas melánicas al nacer es\(4 \times 10^{-5}\).
- Si la tasa de mutación a nuevos alelos melánicos es\(10^{-6}\), asumiendo que el alelo melánico está en equilibrio mutación-selección, ¿cuál es la reducción en la aptitud del heterocigoto? De repente, los niveles de contaminación aumentan dramáticamente en nuestra población, y la depredación por halcones ofrece ahora una ventaja igual (y opuesta) a los individuos oscuros, ya que alguna vez ofrecía a los individuos normalmente pigmentados.
- ¿Cuál es la probabilidad de que se pierda una sola copia de este alelo (presente una sola vez en la población)?
- Si el tamaño poblacional de nuestras ardillas es de un millón de individuos, y está en equilibrio mutación-selección, ¿cuál es la probabilidad de que la población se adapte de uno o más alelos del charco permanente de alelos melánicos?
Encuentras que la diversidad genética por parejas en humanos es\(0.0005\) /bp y en cucarachas es\(0.01\) /bp. Supongamos que en ambas especies la tasa de mutación es de aproximadamente\(\mu = 2 \times 10^{-8}\) /bp/generación en ambas especies. Supongamos que introduce una mutación deletérea en cada población con un coeficiente selectivo de\(s=10^{-6}\). Calcular la probabilidad de que este alelo se fije en humanos y cucarachas, dado que el alelo comienza en una copia (a frecuencia\(\frac{1}{2N}\)). Compara tu respuesta con la probabilidad neutra de que el alelo mutante tenga una fijación en ambos casos.


