5.4: Pruebas de correlaciones evolutivas

Hay muchas maneras de probar las correlaciones evolutivas entre dos personajes. Los métodos tradicionales como PIC y PGLS funcionan muy bien para probar la regresión evolutiva, que es muy similar a probar correlaciones evolutivas. Sin embargo, cuando se utilizan esos métodos, la conexión con modelos reales de evolución de personajes puede permanecer opaca. Así, primero presentaré enfoques para probar la evolución correlacionada basada en la selección de modelos usando análisis AIC y bayesiano. Después volveré a los métodos “estándar” para la regresión evolutiva al final del capítulo.

Sección 5.4a: Prueba de correlaciones de caracteres usando máxima verosimilitud y AIC

Para probar una correlación evolutiva entre dos caracteres, estamos realmente interesados en los elementos de la matriz R. Para dos caracteres, x e y, R se puede escribir como:

(eq. 5.8)

\[ \mathbf{R} = \begin{bmatrix} \sigma_x^2 & \sigma_{xy} \\ \sigma_{xy} & \sigma_y^2 \\ \end{bmatrix} \]

Nos interesa el parámetro σ _{x y} -la covarianza evolutiva- y si es igual a cero (sin correlación) o no. Una forma sencilla de probar esta hipótesis es establecer dos hipótesis competitivas y compararlas entre sí. Una hipótesis (H ₁) es que los rasgos evolucionan independientemente unos de otros, y otra (H ₂) que los rasgos evolucionan con alguna covarianza σ _{x y}. Podemos escribir estas dos matrices de tasas como:

(eq. 5.9)

\[ \begin{array}{lcr} \mathbf{R}_{H_1} = \begin{bmatrix} \sigma_x^2 & 0 \\ 0 & \sigma_y^2 \\ \end{bmatrix} & \mathbf{R}_{H_2} = \begin{bmatrix} \sigma_x^2 & \sigma_{xy} \\ \sigma_{xy} & \sigma_y^2 \\ \end{bmatrix}\\ \end{array} \]

Podemos calcular una estimación ML de los parámetros en RH ₂ usando la ecuación 5.4. La estimación de máxima verosimilitud de _RH1 se puede obtener señalando que, si la evolución de caracteres es independiente en todos los caracteres, entonces ambos σ _x ² y σ _y ² se puede obtener tratando cada carácter por separado y usando ecuaciones del capítulo 3 para resolver para cada uno. Resulta que las estimaciones ML para σ _x ² y σ _y ² son siempre exactamente las mismas para H ₁ y H ₂.

Para comparar estos dos modelos, calculamos la probabilidad de cada uno utilizando la ecuación 5.4. Luego podemos comparar estas dos probabilidades usando una prueba de razón de verosimilitud o comparando las puntuaciones de AICc (ver capítulo 2).

Figura 5.3. La relación entre la masa corporal de los mamíferos y el tamaño del hogar. Para ilustrar el efecto de contabilizar un árbol, se traza una línea sólida para la línea de regresión a partir de un análisis estándar, y una línea punteada de PGLS, que utiliza el árbol filogenético. Estos métodos se discuten con más detalle en la siguiente sección. Imagen del autor, puede ser reutilizada bajo licencia CC-BY-4.0.

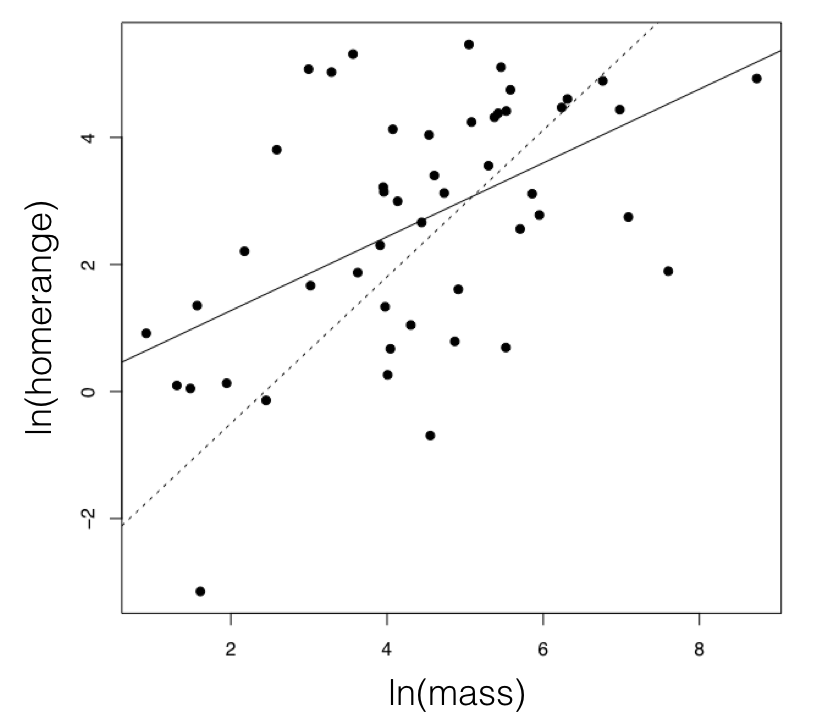
Para el ejemplo de mamíferos, podemos considerar los dos rasgos del tamaño corporal (transformado en ln) y el tamaño del rango del hogar (Garland 1992). Estos dos caracteres tienen una correlación positiva mediante el análisis de regresión estándar (r = 0.27), y una regresión lineal es significativa (P = 0.0001; Figura 5.3). Si ajustamos un modelo de movimiento browniano multivariado a estos datos, considerando el rango hogareño como rasgo 1 y la masa corporal como rasgo 2, obtenemos las siguientes estimaciones de parámetros:

(eq. 5.10)

\[ \begin{array}{cc} \hat{\mathbf{a}}_{H_2} = \begin{bmatrix} 2.54 \\ 4.64 \\ \end{bmatrix} & \hat{\mathbf{R}}_{H_2} = \begin{bmatrix} 0.24 & 0.10 \\ 0.10 & 0.09 \\ \end{bmatrix}\\ \end{array} \]

Obsérvese el elemento positivo fuera de la diagonal en la matriz R estimada, sugiriendo una correlación evolutiva positiva entre estos dos rasgos. Este modelo corresponde a la hipótesis 2 anterior, y tiene una probabilidad logarítmica de l n L = −164.0. Si ajustamos un modelo sin correlación entre los dos rasgos, obtenemos:

(eq. 5.11)

\[ \begin{array}{cc} \hat{\mathbf{a}}_{H_1} = \begin{bmatrix} 2.54 \\ 4.64 \\ \end{bmatrix} & \hat{\mathbf{R}}_{H_1} = \begin{bmatrix} 0.24 & 0 \\ 0 & 0.09 \\ \end{bmatrix}\\ \end{array} \]

Cabe señalar nuevamente que solo las estimaciones de la correlación evolutiva se vieron afectadas por esta restricción del modelo; todas las demás estimaciones de parámetros siguen siendo las mismas. Este modelo tiene una probabilidad logarítmica más pequeña (más negativa) de l n L = −180.5.

Una prueba de razón de verosimilitud da Δ = 33.0, y P < <0.001, rechazando la hipótesis nula. La diferencia en las puntuaciones A I C _c es 30.9, y el peso Akaike para el modelo 2 es efectivamente 1.0. Todas las formas de comparar estos dos modelos dan fuerte apoyo a la hipótesis 2. Podemos concluir que existe una correlación evolutiva entre la masa corporal y el tamaño del rango del hogar en mamíferos. Lo que esto significa en términos evolutivos es que, a través de los mamíferos, los cambios evolutivos en la masa corporal tienden a covariar positivamente con los cambios en el rango del hogar.

Sección 5.4b: Pruebas de correlaciones de caracteres mediante selección de modelos bayesianos

También podemos implementar un enfoque bayesiano para probar la evolución correlacionada de dos personajes. La forma más sencilla de hacerlo es simplemente usar el algoritmo estándar para MCMC bayesiano para ajustar un modelo correlacionado a los dos caracteres. Podemos modificar el algoritmo presentado en el capítulo 2 de la siguiente manera:

1. _{Muestree un conjunto de valores de parámetros iniciales σ x ², σ y 2, σ x y, $\ bar {z} _1 (0) $ y $\ bar {z} _2 (0) $ de distribuciones anteriores.} Para este ejemplo, podemos establecer nuestra distribución anterior como uniforme entre 0 y 1 para σ _x ² y σ _y ², uniforme de -1 a +1 para σ _{x y}, uniforme de 1 a 9 para $\ bar {z} _1 (0) $ (LnMASs), y -3 a 5 para $\ bar {z} _1 (0) $ (LnHomeRange).
2. Dados los valores actuales de los parámetros, seleccione nuevos valores de parámetros propuestos utilizando la densidad propuesta Q (p ′| p). Aquí, para los cinco valores de parámetros, utilizaremos una densidad de propuesta uniforme con ancho 0.2, de manera que Q (p ′| p) ∼ U (p − 0.1, p + 0.1).
3. Calcula tres proporciones:

• El odds ratio anterior, R _{p r i o r}. Esta es la relación de la probabilidad de dibujar los valores de los parámetros p y p' del anterior. Dado que nuestros antecedentes son uniformes, R _{p r i o r} = 1.
• La relación de densidad propuesta, R _{p r o p o s a l}. Esta es la relación de probabilidad de propuestas que van de p a p' y a la inversa. Nuestra densidad propuesta es simétrica, de manera que Q (p ′| p) = Q (p | p ′) y R _{p r o p o s a l} = 1.
• El cociente de verosimilitud, R _{l i k e l i h o o d}. Esta es la relación de probabilidades de los datos dados los dos valores de parámetros diferentes. Podemos calcular estas probabilidades a partir de la ecuación 5.6 anterior (eq. 5.12).
  \ [R_ {verosimilitud} =\ frac {L (P'|d)} {L (P|d)} =\ frac {P (d|P')} {P (d|P)}\ [

4. Encuentre R _{a c c e p t}, el producto de las probabilidades previas, la relación de densidad propuesta y la razón de verosimilitud. En este caso, tanto las probabilidades previas como las relaciones de densidad propuesta son 1, por lo que R _{a c c e p t} = R _{l i k e l i h o d}.
5. Dibuja un número aleatorio x de una distribución uniforme entre 0 y 1. Si x < R _{a c c e p t}, acepte el valor propuesto de todos los parámetros; de lo contrario rechace, y conserve los valores actuales de los parámetros.
6. Repita los pasos 2-5 una gran cantidad de veces.

Luego podemos inspeccionar la distribución posterior para que el parámetro sea significativamente mayor que (o menor que) cero. Como ejemplo, dirigí este MCMC durante 100 mil generaciones, descartando las primeras 10 mil generaciones como burn-in. Luego muestreé la distribución posterior cada 100 generaciones, y obtuve las siguientes estimaciones de parámetros: $\ hat {\ sigma} _x^2 = 0.26$ [intervalo creíble (IC) 95%: 0.18 - 0.38], $\ hat {\ sigma} _y^2 = 0.10$ (IC 95%: 0.06 -0.15), y $\ hat {\ sigma} _ {xy} = 0.11$ (IC 95%: 06 - 0.17; ver Figura 5.4). Estos resultados son comparables a nuestras estimaciones de ML. Además, el IC 95% para σ _{x y} no se solapa con 0; de hecho, ninguna de las 901 muestras posteriores de σ _{x y} es menor que cero. Nuevamente, podemos concluir con confianza que existe una correlación evolutiva entre estos dos personajes.

Sección 5.5c: Pruebas de correlaciones de caracteres usando enfoques tradicionales (PIC, PGLS)

El enfoque descrito anteriormente, que prueba una correlación evolutiva entre caracteres utilizando la selección de modelos, no se aplica típicamente en la literatura de biología comparada. En cambio, la mayoría de las pruebas de correlación de caracteres se basan en la regresión filogenética utilizando uno de dos métodos: contrastes filogenéticos independientes (PIC) y mínimos cuadrados filogenéticos generales (PGLS). PGLS es en realidad matemáticamente idéntico a los PIC en el caso simple descrito aquí, y más flexible que los PIC para otros modelos y tipos de caracteres. Aquí revisaré tanto PIC como PGLS y explicaré cómo funcionan y cómo se relacionan con los modelos descritos anteriormente.

Los contrastes filogenéticos independientes pueden ser utilizados para realizar una prueba de regresión para la relación entre dos caracteres diferentes. Para ello, se calculan los PIC estandarizados para el rasgo x y el rasgo y. Luego se usa regresión lineal estándar forzada a través del origen para probar una relación entre estos dos conjuntos de PIC. Es necesario forzar la regresión a través del origen porque la dirección de resta de los contrastes a través de cualquier nodo del árbol es arbitraria; una reflexión de todos los contrastes a través de ambos ejes simultáneamente no debería tener efecto en los análisis ³.

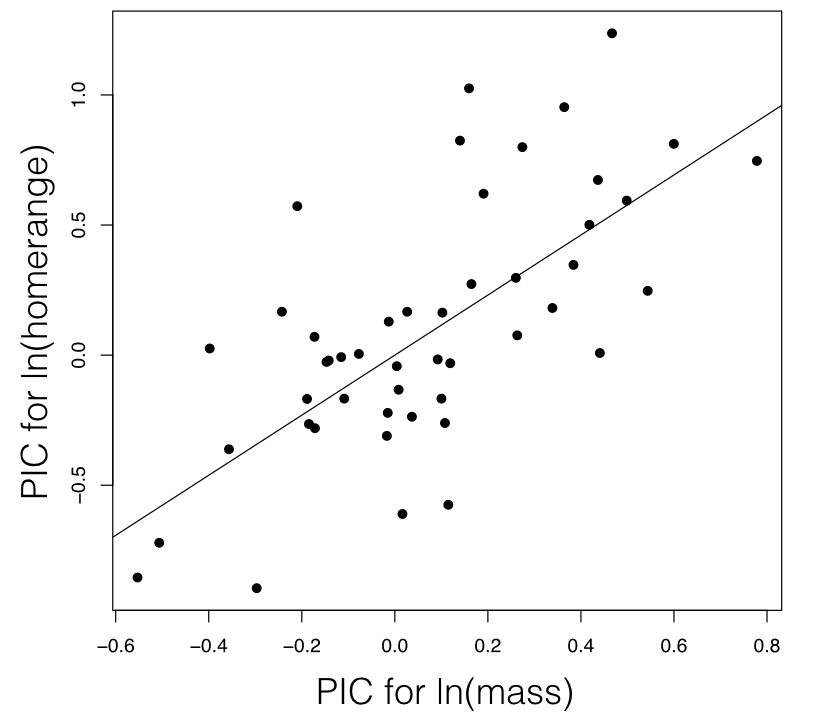
Para el homerange y la masa corporal de mamíferos, una prueba de regresión PIC muestra una correlación significativa entre los dos rasgos (P < <0.0001; Figura 5.5).

Figura 5.4. Regresión basada en contrastes independientes. La línea de regresión es forzada a través del origen. Imagen del autor, puede ser reutilizada bajo licencia CC-BY-4.0.

Hay un inconveniente en el análisis de regresión PIC, aunque —no se recupera una estimación de la intercepción de la regresión de y sobre x — es decir, el valor de y uno esperaría cuando x = 0. La forma más fácil de obtener esta estimación de parámetros es usar en su lugar mínimos cuadrados filogenéticos generalizados (PGLS). El PGLS utiliza la maquinaria estadística común de mínimos cuadrados generalizados y la aplica a datos comparativos filogenéticos. En mínimos cuadrados generalizados normales, se construye un modelo de la relación entre y y x, como:

(eq. 5.13)

y = X _D b +

Aquí, y es un vector n × 1 de valores de rasgo y b es un vector de coeficientes de regresión desconocidos que deben estimarse a partir de los datos. X _D es una matriz de diseño que incluye los rasgos que uno desea probar para una correlación con y y, si el modelo incluye una intercepción, una columna de 1s. Para probar correlaciones, utilizamos:

(eq. 5.14)

\[ \mathbf{X_D} = \begin{bmatrix} 1 & x_1 \\ 1 & x_2 \\ \dots & \dots \\ 1 & x_n \\ \end{bmatrix} \]

En el caso de un predictor y una variable de respuesta, b es 2 × 1 y el modelo resultante se puede utilizar para probar correlaciones entre dos caracteres. Sin embargo, X _D también podría ser multivariante, y puede incluir más de un carácter que podría estar relacionado con y. Esto nos permite llevar a cabo el equivalente de regresión múltiple en un contexto filogenético. Finalmente, son los residuales, la diferencia entre los valores y predichos por el modelo y sus valores reales. En la regresión tradicional, se supone que los residuos están todos distribuidos normalmente con la misma varianza. Por el contrario, con GLS, se asume que los residuales podrían no ser independientes entre sí; en cambio, son multivariados normales con cero promedio esperado y alguna matriz de varianza-covarianza Ω.

En el caso del movimiento browniano, podemos modelar los residuos como teniendo varianzas y covarianzas que siguen la estructura del árbol filogenético. En otras palabras, podemos sustituir nuestra matriz de varianza-covarianza filogenética C como la matriz Ω. Luego podemos realizar análisis GLS estándar para estimar los parámetros del modelo:

(eq. 5.15)

\[ \hat{\mathbf{b}} = (\mathbf{X}_D ^ \intercal \mathbf{\Omega}^{-1} \mathbf{X}_D ^ \intercal)^{-1} \mathbf{X}_D ^ \intercal \mathbf{\Omega}^{-1} \mathbf{y} = (\mathbf{X}_D ^ \intercal \mathbf{C}^{-1} \mathbf{X}_D ^ \intercal)^{-1} \mathbf{X}_D ^ \intercal \mathbf{C}^{-1} \mathbf{y} \]

El primer término en $\ hat {\ mathbf {b}} $ es la media filogenética $\ bar {z} (0) $. El otro término en $\ hat {\ mathbf {b}} $ será una estimación para la pendiente de la relación entre y y x, cuyo cálculo controla estadísticamente el efecto de las relaciones filogenéticas.

La aplicación de PGLS a la masa corporal de los mamíferos y al rango del hogar da como resultado una estimación idéntica de la pendiente y el valor P a la que obtenemos usando contrastes independientes. PGLS también devuelve una estimación de la intercepción de esta relación, que no se puede obtener de los PIC.

Por supuesto, otra diferencia es que los PIC y PGLS utilizan regresión, mientras que el enfoque descrito anteriormente prueba una correlación. Estos dos tipos de pruebas estadísticas son diferentes. Pruebas de correlación para una relación entre x e y, mientras que la regresión intenta encontrar la mejor manera de predecir y a partir de x. Para correlación, no importa a qué variable llamemos x y a cuál llamemos y. Sin embargo, en regresión obtendremos una pendiente diferente si predecimos y dado x en lugar de predecir x dado y. El modelo que asumen los modelos de regresión filogenética también es diferente del modelo anterior, donde asumimos que los dos personajes evolucionan bajo un modelo de movimiento browniano correlacionado. Por el contrario, PGLS (e implícitamente, PICs) asumen que las desviaciones de cada especie de la línea de regresión evolucionan bajo un modelo de movimiento browniano. Podemos imaginar, por ejemplo, que las especies pueden deslizarse libremente a lo largo de la línea de regresión, pero que evolucionar alrededor de esa línea puede ser capturada por un modelo browniano normal. Otra forma de pensar sobre un modelo PGLS es que estamos tratando x como una propiedad fija de especies. La desviación de y de lo que se predice por x es lo que evoluciona bajo un modelo de movimiento browniano. Si esto parece extraño, ¡es porque lo es! Existen otros modelos más complejos para modelar la evolución correlacionada de dos personajes que hacen suposiciones más evolutivamente realistas (por ejemplo, Hansen 1997); volveremos a este tema más adelante en el libro. Al mismo tiempo, el PGLS es un método bien utilizado para la regresión evolutiva, y es indudablemente útil a pesar de sus suposiciones algo extrañas.

El análisis de PGLS, como se describió anteriormente, asume que podemos modelar la estructura de error de nuestro modelo lineal como evolucionando bajo un modelo de movimiento browniano. Sin embargo, se puede cambiar la estructura de la matriz de varianza-covarianza de error para reflejar otros modelos de evolución, como Ornstein-Uhlenbeck. Volvemos a este tema en un capítulo posterior.