5.2: Enzimas

Para 1941, sus estudios correlacionando mutaciones con deficiencias enzimáticas en Neurospora crassa (moho del pan) y Drosophila melanogaster llevaron a George Beadle y Edward Tatum a proponer la hipótesis de un gen/una enzima en 1941. En 1958, compartieron el Premio Nobel de Fisiología y Medicina por esta obra. En el momento del premio, su hipótesis se había transformado dos veces: primero en el ein de un gen/uno-prot, y luego en la hipótesis de un gen/uno-polipéptido. Esta historia legítimamente venerada ayudó a lanzar la era de la biología molecular, ¡haciendo que el descubrimiento de los catalizadores de ARN fuera una gran sorpresa! El descubrimiento de catalizadores de ARN, apodados ribozimas, le valió a Sidney Altman y Thomas Cech el Premio Nobel de Química en 1989. Ahora se conocen ribozimas que catalizan el empalme de ARN (la eliminación de regiones no deseadas de un ARN precursor. Las ribozimas también se asocian con una región de ARN ribosómico, donde participan en la catálisis de la síntesis de proteínas. Aquí, el enfoque aquí se basa en la larga historia de catálisis de enzimas proteicas, pero se debe reconocer que los mecanismos de los mecanismos catalíticos enzimáticos a discutir involucran características esenciales en todos los biocatalizadores.

Las enzimas son generalmente solubles dentro o fuera de las células, mientras que algunas son parte de membranas u otras estructuras celulares. En todos los casos, se unen a sustratos solubles (los reactivos en reacciones catalizadas por enzimas). El gran tamaño y la exquisita diversidad de estructuras proteicas hacen que las enzimas sean catalizadores altamente específicos. La especificidad de una enzima es el resultado de la forma del sitio activo de la enzima, que depende de la disposición tridimensional de los aminoácidos dentro y alrededor de la región. Los sustratos de una reacción bioquímica catalizada se unen y mantienen en su lugar sobre la enzima mientras se realizan reordenamientos rápidos de enlaces. Debido a su flexibilidad, las enzimas experimentan cambios de forma en el sitio activo durante la catálisis misma. Además, esta flexibilidad permite que pequeños metabolitos en las células interactúen y cambien las formas de muchas enzimas. Este último fenómeno permite la regulación alostérica, permitiendo a las células controlar las tasas e incluso la dirección de las reacciones y vías bioquímicas. Como veremos, las enzimas también pueden estar unidas a grupos protésicos o iones que contribuyen a la forma y actividad de la enzima.

Casi no se produce ninguna reacción química que no sea directamente el resultado de la catálisis enzimática, desde la digestión de nutrientes en la boca, estómago e intestino delgado hasta prácticamente todas las reacciones químicas dentro de sus células [echa un vistazo a Kornberg A (1989) Never a Dull Enzyme. Ann. Rev. Biochem. 58:1-30].

A. Mecanismos de la Catálisis Enzimática

Describimos la acción de la catálisis biológica de dos maneras. Una forma toma en cuenta las características estructurales de la enzima (forma del sitio activo, conformación general, las afinidades de la enzima por sus sustratos). La otra forma implica la energía de la acción enzimática. Veremos que las enzimas bajan la energía de activación de una reacción química. La energía de activación es una barrera energética inherente a la reacción. Por supuesto, las consideraciones estructurales y energéticas de la catálisis enzimática están relacionadas.

1. Consideraciones estructurales de la catálisis

De un curso de química, puede recordar que la velocidad de una reacción no catalizada depende de la concentración de los reactivos en solución. Se trata de la Ley de Acción de Masas, reconocida en el siglo XIX. Mira esta simple reacción:

\[\ce{A + B <=> C + D}\]

La Ley de Acción de Masas hace dos supuestos clave:

1. En cualquier momento dado después del inicio de la reacción, la velocidad de formación del producto es proporcional a las concentraciones de los reactivos y productos ([A], [B], [C] y [D] en este caso).
2. Las reacciones químicas en el laboratorio finalmente alcanzan el equilibrio, momento en el que la velocidad neta de formación de los productos de reacción es cero (es decir, las reacciones directa e inversa ocurren a la misma velocidad).

Al inicio de la reacción escrita anteriormente, dado que aún no hay productos, la velocidad de reacción debe ser directamente proporcional solo a la concentración de los reactivos. Por lo tanto, la Ley de Acción de Masas predice que una reacción química ocurrirá más rápido a concentraciones más altas de A y B. Esto se debe a que hay más moléculas reaccionantes en solución y una mayor probabilidad de que colisionen en una orientación que permita los reordenamientos de enlaces para el reacción a ocurrir.

Por supuesto, las concentraciones de reactivos disminuyen a medida que los productos se acumulan con el tiempo. Entonces la velocidad de formación de C & D debería ralentizarse, ahora afectada por las concentraciones de producto así como de reactivos; recuerde, ¡todas las reacciones químicas son inherentemente reversibles! Puede reconocer las ecuaciones de velocidad química de un curso de química; estas permiten cuantificar las velocidades de reacción para nuestra reacción de muestra. Aquí está la tasa de formación de los productos, C y D:

\[\text{Rate of formation of products (C & D)} = \mathrm{k_1[A][B] – k_{-1}[C][D]}\]

Esta ecuación reconoce que la reacción es reversible. Por lo tanto, la velocidad de reacción neta es igual a la velocidad de la reacción directa\(\ce{k_1[A][B]}\) menos la velocidad de la reacción inversa\(\ce{k_{-1}[C][D]}\). La ecuación es válida (aplicable) en cualquier momento durante la reacción. \(\ce{k_1}\)y\(\ce{k_{-1}}\) son constantes de velocidad para las reacciones hacia adelante y hacia atrás, respectivamente.

Entonces, ¿cómo funcionan los catalizadores? Los catalizadores aumentan las velocidades de reacción química al unir los reactivos más rápidamente de lo que se encontrarían basándose solo en el movimiento molecular aleatorio en solución. Esto es posible porque los catalizadores tienen afinidad por sus sustratos.

En el caso de los catalizadores inorgánicos, las fuerzas genéricas relativamente débiles explican la afinidad de los reactivos y los catalizadores inorgánicos. Así, un catalizador metálico (por ejemplo, plata, platino) atrae moléculas con la configuración apropiada (por ejemplo, carga). Si la atracción (afinidad) es suficiente, el metal mantendrá los reactivos en su lugar el tiempo suficiente para catalizar los reordenamientos de enlaces de una reacción química.

A diferencia de los catalizadores inorgánicos, las enzimas han evolucionado formas altamente específicas con propiedades físico-químicas. Como resultado, las enzimas suelen atraer solo los sustratos necesarios para una reacción bioquímica particular. El sitio activo de una enzima tiene la afinidad exquisitamente selectiva por su (s) sustrato (s). Esta afinidad es muchas veces mayor que la de los catalizadores inorgánicos para reactivos genéricos. El resultado es que las enzimas son catalizadores más eficientes, más rápidos.

Las primeras ideas sobre cómo la interacción sustrato-enzima podría ser tan específica sugirieron un mecanismo de cerradura y llave, ilustrado a continuación.

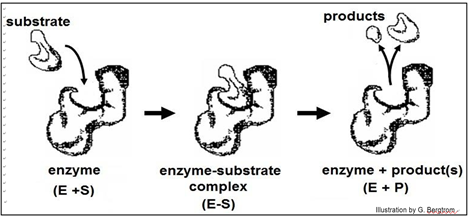
Según este modelo, la afinidad de la enzima por el sustrato los une, después de lo cual el sustrato encaja de manera única en el sitio activo como una llave en una cerradura. Una vez en el sitio activo, el sustrato (s) sufriría los reordenamientos de enlaces específicos para la reacción catalizada para generar productos y regenerar una enzima inalterada. Pero la cristalografía de rayos X de la interacción enzima-sustrato reveló que el sitio activo de la enzima cambia de forma durante la catálisis. Este cambio alostérico sugirió el mecanismo revisado de ajuste inducido de acción enzimática modelado a continuación.

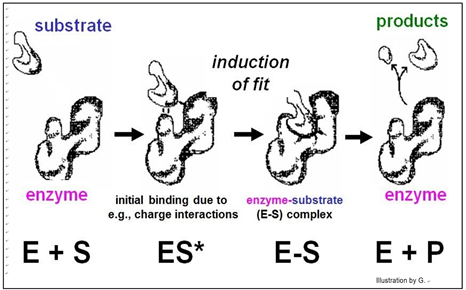
En este modelo, la afinidad enzima-sustrato hace que el sustrato se una a la superficie de la enzima. Una vez unida, la enzima sufre un cambio alostérico, atrayendo el sustrato (s) más firmemente al sitio activo y catalizando la reacción. Por supuesto, después de que los productos de reacción se desprenden, la enzima vuelve a su forma original.

2. Consideraciones energéticas de la catálisis

_{Los catalizadores funcionan disminuyendo la energía de activación (E a) para una reacción, aumentando así drásticamente la velocidad de la reacción.} La energía de activación es esencialmente una barrera para unir los sustratos que interactúan para someterse realmente a una reacción bioquímica. Comparar el movimiento aleatorio de sustratos en solución que ocasionalmente se encuentran entre sí. Aún más raramente se topan entre sí de la manera justa para provocar una reacción. Esto explica por qué agregar más reactivos o aumentar la temperatura de una reacción puede acelerarla..., aumentando el número de colisiones moleculares aleatorias así como productivas. A diferencia de las moléculas y reacciones en un tubo de ensayo, los organismos vivos no tienen estas opciones para realizar reacciones bioquímicas rápidas, o controlar las velocidades de reacción.

Las superficies catalíticas inorgánicas atraen reactivos donde puede ocurrir catálisis. Los atractivos son débiles en comparación con los de las enzimas y sus sustratos. El sitio activo de una enzima atrae muy fuertemente sustratos distribuidos aleatoriamente, lo que hace que la catálisis enzimática sea más rápida que la catálisis inorgánica. Nuevamente, las células no pueden usar catalizadores inorgánicos, la mayoría de los cuales son insolubles y atraerían a los reactivos indiscriminadamente... ¡no es una buena manera para que las células controlen el metabolismo El advenimiento de las enzimas con su especificidad y alta tasa de catálisis fue un evento clave en la evolución química requerida para los orígenes de la vida. Como vimos, el cambio alostérico durante la 'inducción de fit' permite catálisis específica. De hecho, una reacción catalizada será más rápida que la misma reacción catalizada por una pieza de metal, y por supuesto mucho más rápida (¡millones de veces más rápida!) que la reacción no catalizada. La energía de la catálisis ayuda a explicar por qué. Echa un vistazo a la energía de una simple reacción en la que A & B se convierten a C & D, que se muestra a continuación.

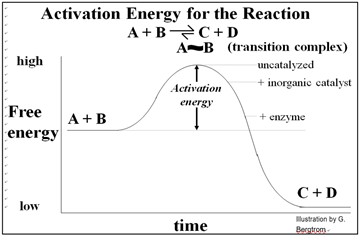
Realizadas en un sistema cerrado, las reacciones catalizadas por enzimas alcanzan su equilibrio más rápidamente. Al igual que con todos los catalizadores, las enzimas no son consumidas por las reacciones que catalizan, ni alteran las concentraciones de equilibrio de los reactivos y productos de estas reacciones. ¡Las aproximadamente 4000 reacciones bioquímicas que se sabe que se catalizan en las células son sin duda una subestimación! Pero recuerda también, ¡que estimamos que el genoma humano solo tiene entre 20,000 y 25,000 genes diferentes!

B. Regulación enzimática

Señalamos que algunas enzimas están reguladas, lo que solo significa que los factores en la célula pueden ralentizar o acelerar su tasa de catálisis. De esta manera, la célula puede responder rápidamente a las necesidades metabólicas reflejadas por los niveles intracelulares de estos factores. Los factores que ralentizan la catálisis se denominan inhibidores. A los que aceleran la catálisis se les llama activadores. Además de responder a indicadores moleculares intracelulares del estado metabólico de la célula, las enzimas pueden ser inhibidas por fármacos, venenos o cambios en el medio químico (por ejemplo, pH). Dado que las reacciones celulares ocurren como parte de las vías bioquímicas, la regulación de una sola enzima puede afectar a una vía completa. Por ejemplo, mira la vía genérica que se ilustra a continuación.

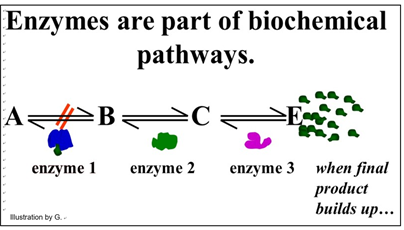
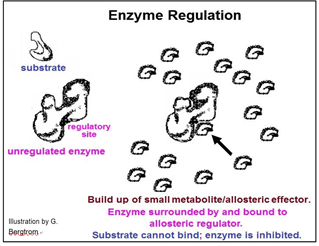
Esta vía existe para producir la sustancia E. En condiciones normales, otra serie de reacciones metabólicas consumiría E. No obstante, si la célula está satisfaciendo sus necesidades metabólicas y ya no necesita tanto E, se acumulará en la célula. Si hay un exceso de E en la célula, podría unirse a una de las enzimas. En la vía mostrada, E se une a la enzima 1. Esta unión provoca un cambio alostérico que inhibe la catálisis y ralentiza toda la ruta. En este ejemplo, de regulación alostérica, podemos suponer que la regulación inhibitoria de la enzima 1 evolucionó para controlar la tasa de producción de la sustancia E. Este es un modo común de regulación alostérica enzimática, llamada inhibición por retroalimentación.

Las enzimas se pueden regular precisamente porque pueden doblarse fuera de forma (¡o en forma para el caso!). Algunos metabolitos pequeños se convierten en información química cuando se acumulan en las células, convirtiéndose en los indicadores del estado metabólico celular. El resultado es una disminución o aumento de las actividades enzimáticas para lograr una respuesta celular adecuada.

Ya sea un activador o un inhibidor de la catálisis enzimática, las moléculas reguladoras normalmente se unen a enzimas en sitios reguladores alostéricos, causando cambios alostéricos locales que se transmiten al sitio activo. La inhibición enzimática ocurrirá si un cambio en la forma reduce la afinidad de la enzima por el sustrato o la velocidad de los reordenamientos de enlaces después de que el sustrato haya entrado en el sitio activo. La activación enzimática se produciría si el efecto alostérico aumentara esta afinidad y/o velocidad catalítica. El mecanismo de regulación alostérica de la actividad enzimática se ilustra a continuación.

Podemos entender los efectos que cambian las tasas de catálisis enzimática determinando la cinética enzimática. Al comparar los datos cinéticos para cada enzima en una ruta bioquímica, se puede determinar una reacción limitante de velocidad estándar bajo un conjunto dado de condiciones. Por ejemplo, si las pruebas clínicas revelan que un paciente está produciendo demasiado metabolito bioquímico, entonces la velocidad catalítica de la enzima normalmente limitante de la velocidad en su vía de síntesis puede haber aumentado. ¿Y entonces qué, si el paciente está produciendo muy poco del metabolito? O bien la velocidad catalítica de la enzima limitante de velocidad ha disminuido o la velocidad catalítica de otra enzima en la ruta bioquímica se ha vuelto limitante de la velocidad. Las razones por las que una bioquímica celular se desviaría de los niveles “normales” incluyen:

1. Infección viral y bacteriana o venenos ambientales: estos pueden interferir con una reacción específica en una vía metabólica; ¡los remedios dependen de esta información!
2. Enfermedad crónica resultante de deficiencias enzimáticas mutacionales: los tratamientos pueden incluir medicamentos diseñados para mejorar o inhibir (según corresponda) la actividad enzimática.
3. Enfermedad genética ligada a la deficiencia metabólica: si una enzima específica es la culpable, podría ser posible investigar un curso de tratamiento pre y/o postnatal.
4. Cambios en el estilo de vida y opciones: estos pueden incluir hábitos alimenticios, generalmente remediados por un cambio en la dieta.
5. Cambios en el estilo de vida producidos por las circunstancias más que por la elección: estos son cambios debidos al envejecimiento, como la posibilidad de aparición de Diabetes Tipo 2; esto puede retrasarse cambiando a una dieta baja en carbohidratos favoreciendo cambios hormonales que mejoren el metabolismo adecuado del azúcar.

Conocer la (s) reacción (es) limitante (es) de velocidad en vías bioquímicas puede identificar enzimas reguladas y conducir a un remedio para corregir un desequilibrio metabólico. Como se señaló, las ribozimas son moléculas de ARN que catalizan reacciones bioquímicas; su cinética también puede analizarse y clasificarse. A continuación, observamos una visión general de la cinética enzimática (para explicaciones claras y detalladas de los mecanismos catalíticos enzimáticos, consulte Jencks WP [1987, Catalysis in Chemistry and Enzimology. Mineola, NY, Courier Dover Publications]). Consideraremos cómo se regulan las enzimas más adelante, cuando discutamos la glucólisis, una vía bioquímica que la mayoría de los seres vivos utilizan para extraer energía de los nutrientes.

C. Cinética enzimática

Todas las reacciones químicas catalizadas muestran cinética de saturación, como se muestra a continuación.

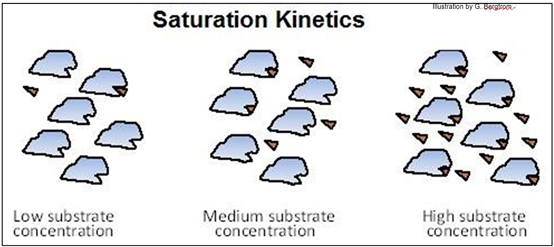
Observe cómo a alta concentración de sustrato, los sitios activos en todas las moléculas enzimáticas se unen a las moléculas de sustrato.

El experimento descrito a continuación determinará la cinética de la conversión de S a P por la enzima E.

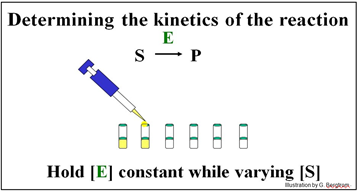
Se configuran una serie de tubos de reacción, cada uno con la misma concentración de enzima ([E]) pero diferentes concentraciones de sustrato ([S]). Se grafica la concentración de P ([P]) producida en diferentes momentos justo después del inicio de la reacción en cada tubo para determinar la velocidad inicial de formación de P para cada concentración de sustrato ensayado (ver más adelante).

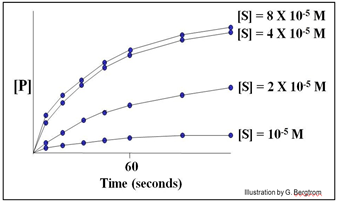
En este ejemplo hipotético, las velocidades de las reacciones (cantidad de P hecha a lo largo del tiempo) no aumentan a concentraciones de sustrato superiores a 4 X10 ^-5 M. Por lo tanto, las curvas superiores representan la velocidad máxima de la reacción a la concentración experimental de enzima. Decimos que la velocidad máxima de reacción ocurre a la saturación.

A continuación, podemos estimar la velocidad de reacción inicial (v _o) a cada concentración de sustrato trazando la pendiente de los primeros puntos de tiempo a través del origen de cada curva en la gráfica. Considera la gráfica a continuación, de las velocidades de reacción iniciales estimadas de esta manera.

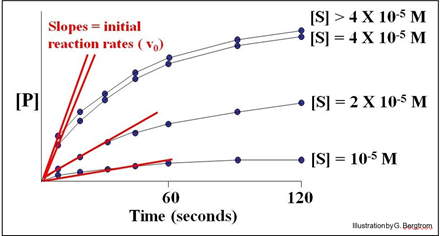
Cada línea recta es el v _o para la reacción en una [S] diferente cerca del comienzo de la reacción, cuando [S] es alta y [P] es muy baja. A continuación, trazamos estas tasas (pendientes, o valores v _o) frente a las diferentes concentraciones de S en el experimento para obtener la curva de la cinética de reacción a continuación.

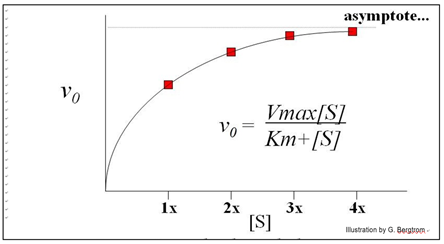
Este es un ejemplo de la cinética de Michaelis-Menten común a muchas enzimas, que lleva el nombre de los dos bioquímicos que se dieron cuenta de que la curva describía la hipérbola rectangular.

Dicho de otra manera, la ecuación describe matemáticamente el mecanismo de catálisis de la enzima. La siguiente ecuación describe matemáticamente una hipérbola rectangular:

\[\mathrm{y = \dfrac{xa}{x + b}}\]

Se te podría pedir que entiendas la derivación de (¡o incluso derivar!) la ecuación de Michaelis- Menten en un curso de Bioquímica. Baste decir aquí que Michaelis y Menten comenzaron con algunas suposiciones simples sobre cómo procedería una reacción catalizada por enzimas y escribieron ecuaciones químicas y de velocidad razonables para esas reacciones. Aquí hay una manera de escribir la ecuación química para una reacción simple en la que una enzima (E) cataliza la conversión del sustrato (S) en producto (P):

\[\ce{S<=>[][E] P}\]

Michaelis y Menten racionalizaron que esta reacción en realidad podría proceder en tres pasos. En cada etapa, E, la enzima se trata como un reactivo en la conversión de S a P. A continuación se muestran las ecuaciones químicas resultantes.

Razonando que la reacción media (la conversión de E-S a E-P) sería la más rápida y, por lo tanto, no sería la reacción de catálisis limitante de velocidad, solo consideraron que la primera y tercera reacciones eran relevantes para determinar la cinética general de la formación del producto. Luego escribieron las siguientes ecuaciones de velocidad solo para estas dos reacciones químicas (como lo haría en un curso introductorio de química):

\[V_\text{E-S formation}=\mathrm{k_{1}[E][S]-k_{-1}[\text{E-S}]}\]

\[V_\text{P formation}=\mathrm{k_2[\text{E-S}]-k_{-2}[E][P]}\]

Ambas ecuaciones describen una línea recta, la cual no describe la cinética de reacción hiperbólica observada. Resolver uno por ejemplo, E-S y sustituir la solución por E-S en la otra ecuación dejó una sola ecuación que también describía una línea recta. Nuevamente, no la esperada hipérbola rectangular. Para llegar a una ecuación de velocidad química consistente con una hipérbola rectangular, Michaelis y Menten hicieron varias suposiciones, entre ellas las realizadas por G. E. Briggs y J. B. S. Haldane sobre cómo se comportarían E, S y P en una reacción catalizada.

Fueron esas suposiciones que les permitieron reescribir cada ecuación, combinarlas y reescribirlas en una sola ecuación matemática que efectivamente describía una hipérbola rectangular. Aquí están las suposiciones de Briggs y Haldane:

Ya hemos visto la ecuación que derivaron Michaelis y Menten y ahora conocida como la ecuación de Michaelis-Menten:

\[\mathrm{v_0 = \dfrac{Vmax[S]}{Km + [S]}}\]

El mensaje para llevar a casa aquí es que los supuestos sobre una reacción catalizada por enzimas son una buena aproximación de cómo procede la reacción a lo largo del tiempo.

Michaelis y Menten definieron Vmax y Km como factores cinéticos clave en las reacciones enzimáticas. En el ejemplo genérico de conversión de sustrato a producto, vimos que aumentar [S] da como resultado una mayor tasa de formación de producto debido a una mayor tasa de encuentros de enzimas y moléculas de sustrato. Sin embargo, en algún momento, aumentar [S] no aumenta aún más la velocidad de reacción inicial. En cambio, v _o asintóticamente se aproxima a un máximo teórico para la reacción, definido como Vmax, la velocidad inicial máxima. Como ya hemos visto, Vmax ocurre cuando todos los sitios activos enzimáticos disponibles están saturados (ocupados por sustrato). En este punto, la velocidad catalítica intrínseca determina la tasa de recambio de la enzima. La concentración de sustrato a la que la velocidad de reacción ha alcanzado ½Vmax se define como K _M (la constante de Michaelis-Menten). El km es una relación de constantes de velocidad que quedan después de reescribir las ecuaciones de velocidad para la reacción catalizada.

Para recapitular, las dos propiedades cinéticas más importantes de una enzima son:

1. la rapidez con la que la enzima se satura con un sustrato particular, que está relacionado con la Km para la reacción, y

2. la velocidad máxima de la reacción catalizada, descrita por el Vmax para la reacción.

Conocer estas propiedades sugiere cómo podría comportarse una enzima en condiciones celulares, y puede mostrar cómo la enzima debe responder a la regulación alostérica por factores inhibidores o activadores naturales..., y a venenos u otros químicos anómalos. Puedes encontrar más detalles de cómo se derivan las ecuaciones cinéticas (un paso necesario para entender cómo funciona la enzima) en cualquier buen libro de texto de bioquímica, o echa un vistazo a la entrada Cinética de Michaelis-Menten en el enlace de Wikipedia de Enzimas.