3.1: Las leyes de la termodinámica
- Page ID
- 53398
Dos conceptos fundamentales rigen la energía en lo que se refiere a los organismos vivos: la Primera Ley de la Termodinámica establece que la energía total en un sistema cerrado no se pierde ni se gana, solo se transforma. La Segunda Ley de la Termodinámica establece que la entropía aumenta constantemente en un sistema cerrado.
Más específicamente, la Primera Ley establece que la energía no puede crearse ni destruirse: sólo puede cambiar de forma. Por lo tanto, a través de todos y cada uno de los procesos, la energía total del universo o cualquier otro sistema cerrado es constante. En un sistema termodinámico simple, esto significa que la energía se transforma ya sea por la transferencia de energía térmica (es decir, calentamiento y enfriamiento de una sustancia) o por la producción de trabajo mecánico (es decir, movimiento). En términos biológicos y químicos, esta idea puede extenderse a otras formas de energía como la energía química almacenada en los enlaces entre átomos de una molécula, o la energía lumínica que puede ser absorbida por las hojas de las plantas.
El trabajo, en este caso, no necesita implicar un mecanismo complicado. De hecho, existe un trabajo realizado por cada molécula en la simple expansión de una masa calentada de moléculas gaseosas (tal como se visualiza por la expansión de un globo calentado, por ejemplo). Esto se expresa matemáticamente como la Relación Termodinámica Fundamental:
en la que\(E\) se encuentra la energía interna del sistema,\(T\) es la temperatura,\(S\) es la entropía,\(p\) es la presión, y\(V\) es el volumen.
A diferencia de la Primera Ley, que se aplica incluso a las partículas dentro de un sistema, la Segunda Ley es una ley estadística —se aplica generalmente a los sistemas macroscópicos. Sin embargo, no excluye variaciones a pequeña escala en la dirección de la entropía a lo largo del tiempo. De hecho, el teorema de Fluctuación (propuesto en 1993 por Evans et al, y demostrado por Wang et al en 2002) establece que a medida que aumenta el tiempo o el tamaño del sistema, la probabilidad de un cambio negativo en la entropía (es decir, ir en contra de la Segunda Ley) disminuye exponencialmente. Entonces, en escalas de tiempo muy pequeñas, existe una probabilidad real de que puedan existir fluctuaciones de entropía contra la Segunda Ley.
La Segunda Ley dicta que la entropía siempre busca aumentar con el tiempo. Entropía es simplemente una palabra elegante para caos o desorden. El estado teórico final o de equilibrio es aquel en el que se maximiza la entropía, y no hay orden a nada en el universo o sistema cerrado. Los procesos espontáneos, aquellos que ocurren sin influencia externa, son siempre procesos que convierten el orden en desorden. Sin embargo, esto no excluye la imposición de orden a un sistema. Examinando la forma matemática estándar de la Segunda Ley:
Sistema ΔS + ΔS entorno = ΔS universo,
donde ΔS universo > 0
muestra que la entropía puede disminuir dentro de un sistema siempre y cuando haya un incremento de igual o mayor magnitud en la entropía del entorno del sistema.
La frase “en un sistema cerrado” es un componente clave de estas leyes, y es con la idea encapsulada en esa frase que la vida puede ser posible. Pensemos en una célula típica: en su vida, construye innumerables moléculas complejas, enormes proteínas y ácidos nucleicos formados a partir de una mezcla de pequeños aminoácidos o nucleótidos, respectivamente. En su superficie, este ejemplo podría parecer un contraejemplo a la segunda ley - claramente pasar de una mezcla de varias moléculas pequeñas a una molécula más grande con componentes unidos y ordenados parecería ser una disminución de la entropía (o un aumento en el orden). ¿Cómo es esto posible con respecto a la segunda ley? Lo es, porque la segunda ley sólo se aplica a los sistemas cerrados. Es decir, un sistema que no gana ni pierde materia ni energía.
El “universo” es un sistema cerrado por definición porque no hay nada fuera de él.
Una célula viva no es un sistema cerrado: tiene entradas y salidas. No obstante, la segunda ley sigue siendo útil si reconocemos que la única forma en que se puede pasar por alto es a través del aporte de energía. Si una célula no puede tomar alimentos (entrada de materia y energía en el sistema) muere, porque la segunda ley requiere que todo finalmente se descomponga en colecciones más aleatorias/caóticas de componentes más pequeños. El orden requerido para sostener la vida (pensar en todas las diferentes moléculas complejas que se mencionaron en el capítulo anterior) es fenomenal. Lo mismo se aplica a nivel organizativo (Figura\(\PageIndex{1}\)) -sin un aporte de energía (en forma de moléculas de alimento para animales o en forma de luz para plantas), el organismo morirá y posteriormente se descompondrá.
Crear moléculas a partir de átomos cuesta energía porque toma una colección desordenada de átomos y los fuerza, a través de enlaces químicos, a posiciones ordenadas y no aleatorias. Asimismo, existe un costo de energía para la formación de macromoléculas a partir de moléculas más pequeñas. Al imponer orden en el sistema, debe haber un aporte asociado de energía. Esto sucede en todos los niveles del sistema: átomos a moléculas, moléculas pequeñas a macromoléculas, grupos de moléculas a orgánulos, etc.
A medida que la reacción de polimerización reduce la entropía, requiere de energía generada (generalmente) por la descomposición de ATP en AMP y PPi, que es una reacción que aumenta la entropía.
¿A dónde va esa energía? Termina en los enlaces que están sosteniendo las moléculas o macromoléculas en su estado ordenado. Cuando tal enlace se rompe, y una molécula se vuelve a convertir en una colección de átomos, se libera energía. La energía en un enlace químico es así energía potencial - es energía almacenada que, cuando se libera, tiene la capacidad de hacer trabajo. Este término, si recuerdas la física de tu escuela secundaria, generalmente se aprende junto con la energía cinética, que es la energía que se está utilizando en el proceso de hacer realmente el trabajo (es decir, mover un objeto de un lugar a otro). El ejemplo clásico es la roca en lo alto de una colina: tiene energía potencial porque está elevada y potencialmente podría bajar. A medida que se baja, tiene energía cinética a medida que se mueve. De manera similar en una célula, la energía potencial en un enlace químico puede liberarse y luego usarse para procesos como unir moléculas más pequeñas en moléculas más grandes, o hacer que un motor molecular gire o se doble, acciones que podrían conducir al bombeo de protones o la contracción de las células musculares, respectivamente.
Volviendo a la segunda ley, esencialmente ordena que descomponer moléculas libere energía y que hacer nuevas moléculas (ir en contra de la tendencia natural hacia el desorden) requiere energía. Cada molécula tiene una energía intrínseca y, por lo tanto, siempre que una molécula esté involucrada en una reacción química, habrá un cambio en la energía de la (s) molécula (s) resultante (s). Parte de este cambio en la energía del sistema será utilizable para hacer trabajo, y esa energía es referida como la energía libre de la reacción. El resto se desprende como calor.
La ecuación de Gibbs describe esta relación como
\[ΔG= ΔH-TΔS \]
donde ΔG es el cambio en la energía libre, ΔH es el cambio en la entalpía (aproximadamente equivalente al calor), T es la temperatura a la que tiene lugar la reacción y ΔS es el cambio en la entropía. Por convención, la liberación de energía libre es un número negativo, mientras que un requisito de entrada de energía se denota con un número positivo. Generalmente, una reacción química en la que ΔG < 0 is a spontaneous reaction (also called an exergonic reaction), while a chemical reaction in which ΔG > 0 no es espontánea (o endergónica). Cuando ΔG = 0, el sistema está en equilibrio. ΔG también se puede expresar con respecto a la concentración de productos y reactivos:
\[ΔG = ΔG^o + RT \ln \left( \dfrac{[P_1][P_2][P_3]...}{[R_1][R_2][R_3]...}\right)\]
Los términos entre corchetes denotan concentraciones, ΔG° es la energía libre estándar para la reacción (tal como se lleva a cabo con una concentración de 1M de cada reactivo, a 298K y a 1 atm de presión), R es la constante del gas (1.985 cal K -1 mol -1), y T es la temperatura en Kelvin. En un sistema más sencillo en el que solo hay dos reactivos y dos productos:
\[\ce{aA + bB <=> cC + dD}\]
la ecuación para el cambio de energía libre se convierte
ΔG = ΔG° + rTLn ([C] c [D] d/[A] a [B] b)
Esto es importante para nosotros como biólogos celulares porque aunque las células no son muy adecuadas para regular las reacciones químicas variando la temperatura o la presión de las condiciones de reacción, pueden alterar relativamente fácilmente las concentraciones de sustratos y productos. De hecho, al hacerlo, incluso es posible impulsar una reacción no espontánea (ΔG > 0) hacia adelante espontáneamente (ΔG < 0) ya sea aumentando la concentración de sustrato (posiblemente transportándolos a la célula) o disminuyendo la concentración del producto (ya sea secretándolos de la célula o utilizándolos como sustratos para una reacción química diferente).
Los cambios en la concentración de sustrato o producto para impulsar una reacción no espontánea son un ejemplo de la idea más general de reacciones de acoplamiento para impulsar reacciones energéticamente desfavorables. Las reacciones endergónicas se pueden acoplar a reacciones exergónicas como una serie de reacciones que en última instancia son capaces de avanzar. El único requisito es que el cambio global de energía libre sea negativo (ΔG < 0). Entonces, asumiendo condiciones estándar (ΔG = ΔG°'), si tenemos una reacción con un cambio de energía libre de +5 kcal/mol, es no espontánea. Sin embargo, si acoplamos esta reacción, a la hidrólisis de ATP por ejemplo, entonces ambas reacciones procederán porque el cambio estándar de energía libre de la hidrólisis de ATP a ADP y fosfato es un exergónico -7.3 kcal/mol. La suma de los dos valores ΔG es de -2.3 kcal/mol, lo que significa que la serie acoplada de reacciones es espontánea.
De hecho, el ATP es la “moneda” energética más común en las células precisamente porque el cambio de energía libre de -7.3 kcal/mol de su hidrólisis es suficiente para ser útil para impulsar muchas reacciones endergónicas por acoplamiento, pero es menos costoso (energéticamente) de hacer que otros compuestos que potencialmente podrían liberar aún más energía (por ejemplo, fosfoenolpiruvato, PEP). Además, gran parte de los -14.8 kcal/mol (ΔG°') de la hidrólisis de PEP se desperdiciaría porque relativamente pocas reacciones endergónicas son tan desfavorables que necesitan tanta energía libre.
¿Por qué el ATP es diferente de otros compuestos fosforilados pequeños? ¿Cómo es que el enlace γ-fosfoanhídrido (el más distal) del ATP puede producir tanta energía cuando la hidrólisis de glicerol-3-fosfato produce menos de un tercio de la energía libre? El más obvio es la repulsión electrostática. Aunque se mantienen unidos por los enlaces covalentes, hay muchas cargas negativas en un espacio pequeño (cada fosfato lleva aproximadamente 4 cargas negativas). La eliminación de uno de los fosfatos reduce significativamente la repulsión electrostática. Teniendo en cuenta que la DG se calcula a partir del equilibrio tanto de reactivos como de productos, también vemos que los productos de la hidrólisis de ATP, ATP y fosfato, son muy estables debido a la resonancia (tanto ADP como Pi tienen mayor estabilización de resonancia) y estabilización por hidratación. La mayor estabilidad de los productos significa un mayor cambio de energía libre.
Incluso cuando una reacción es energéticamente favorable (ΔG < 0), puede que no ocurra sin un poco de “empuje”, químicamente hablando. El “empuje” es algo llamado energía de activación, y supera la estabilidad termodinámica. Considera la glucosa, por ejemplo. Este azúcar simple es la principal fuente de energía para todas las células y la energía inherente dentro de sus enlaces se libera a medida que se descompone en dióxido de carbono y agua. Dado que se trata de una molécula grande que se descompone en otras más pequeñas, se incrementa la entropía, así se libera energía de la reacción, y es técnicamente una reacción espontánea. No obstante, si consideramos un poco de glucosa en un platillo en el banco de laboratorio, es evidente que no se va a descomponer espontáneamente a menos que agreguemos calor. Una vez que agreguemos suficiente energía térmica, podemos eliminar la fuente de energía, pero el azúcar continuará descomponiéndose por oxidación (quemadura) a CO 2 y H 2 O.
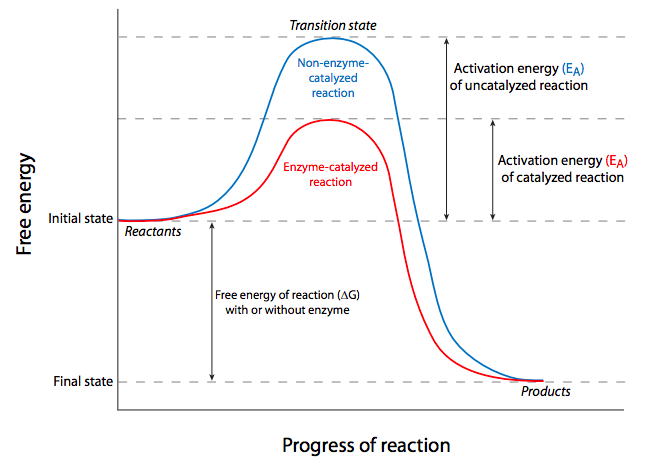
Dicho de otra manera, el (los) reactivo (s) debe (n) llevarse a un estado de energía inestable, conocido como el estado de transición (como se muestra en el pico de las gráficas de la Figura\(\PageIndex{2}\)). Esta barrera de requerimiento energético ante la ocurrencia de una reacción espontánea favorecida termodinámicamente se denomina energía de activación. En las células, el requerimiento de energía de activación significa que la mayoría de las reacciones químicas se producirían con demasiada lentitud o poca frecuencia para permitir todos los procesos que mantienen vivas a las células porque la energía requerida probablemente provendría de la posibilidad de que dos reactivos se estrellaran entre sí con suficiente energía, generalmente significando deben ser calentados. Nuevamente, las células generalmente no son capaces de encender algún quemador Bunsen microscópico para generar la energía de activación necesaria, debe haber otra manera. De hecho, las células superan el problema de la energía de activación mediante el uso de catalizadores para sus reacciones químicas. Ampliamente definido, un catalizador es una sustancia química que aumenta la velocidad de una reacción, puede interactuar transitoriamente con los reactivos, pero no es alterada permanentemente por ellos. El catalizador se puede reutilizar porque es el mismo antes de que comience la reacción, y después de que se complete la reacción. Desde un punto de vista termodinámico, disminuye la energía de activación de la reacción, pero no cambia el ΔG. Por lo tanto, no puede hacer que una reacción no espontánea proceda; sólo puede hacer que una reacción ya espontánea ocurra con mayor rapidez o más frecuencia.


