3.3: Cinética enzimática
- Page ID
- 53390
A diferencia de las reacciones no catalizadas (pero que ocurren fácilmente), en las que la velocidad de la reacción depende solo de la concentración de los reactivos, la velocidad de las reacciones catalizadas por enzimas está limitada por el número de moléculas enzimáticas disponibles. Esta tasa máxima de recambio de sustrato a producto es una función de la velocidad de la enzima y del número de moléculas enzimáticas. \(V_{max}\), esta velocidad o reacción máxima teórica, se aborda cuando existe una concentración tan alta de moléculas de sustrato que no solo está ocupada cada enzima disponible en un momento dado, sino que tan pronto como una enzima termina de convertir sustrato en producto, inmediatamente se une a un nuevo sustrato. Otro término, Km, se relaciona con\(V_{max}\) en que\(K_m\) (la constante de Michaelis) es la concentración de sustrato a la que\(V_{max}/2\) se produce la velocidad de reacción semimáxima. Estos dos términos están relacionados en la ecuación de Michaelis-Menten, que describe la velocidad de reacción\(v\) con respecto a la concentración de sustrato [S].
\[v = \frac { V _ { \max } [ \mathrm { S } ] } { \mathrm { K } _ { \mathrm { M } } + [ \mathrm { S } ] } \label{Michaelis-Menten}\]
La ecuación de Michaelis-Menten fue derivada por Leonor Michaelis y su estudiante de posgrado Maud Menten en 1913, basada en el trabajo de Victor Henri, y es aplicable únicamente a la cinética enzimática simple en la que solo hay un sustrato que se cambia inmediatamente a un producto durante la reacción sin formar ningún compuesto intermedio, la enzima en cuestión no muestra alostericidad, y la reacción es unidireccional.
Cabe señalar que la velocidad de reacción v es en realidad la velocidad de reacción inicial a una concentración de sustrato particular, y a veces se denota v o. Naturalmente, a medida que la reacción continúa, la concentración de sustrato disminuye, junto con la velocidad de reacción.
La ecuación de Michaelis-Menten asume una simple reacción de la forma:
\[\ce{E + S <=> ES -> E +P}\]
donde\(E\) es una enzima,\(S\) es el sustrato, y\(P\) es el producto. Obsérvese la formación del complejo intermedio enzima-sustrato, ES, que es un estado de transición (recordar Figura\(\PageIndex{2}\)) en el que el sustrato es inestable y se asocia con la enzima. De hecho,\(ES\) podría considerarse tan fácilmente\(EP\), ya que este estado es esencialmente el punto de inflexión entre la conversión de sustrato a producto. En esta construcción, la constante de Michaelis\(K_M\),, de una reacción catalizada por enzimas es (k 2 + k 3)/k 1. Esa es la tasa de disociación de ES sobre la tasa de asociación de ES. \(K_M\), por supuesto, varía no sólo dependiendo de la enzima, sino también con respecto a la identidad del sustrato. Algunas enzimas pueden trabajar con múltiples sustratos, y la\(K_M\) de esa enzima para los diferentes sustratos suele ser diferente. Debido a que la curva de saturación en la Figura\(\PageIndex{5}\) puede ser difícil de trabajar, se desarrollaron linealizaciones de la ecuación de Michaelis-Menten (Ecuación\ ref {Michaelis-Menten}). La más común es la trama doble recíproca, mejor conocida como la gráfica Lineweaver-Burk. En este tipo de representación gráfica de la cinética enzimática, se grafica el recíproco de la concentración de sustrato frente al recíproco de la velocidad de reacción. Esto genera una línea en la que la intercepción x es entonces\(-1/K_m\), la intercepción y es\(1/V_{max}\), y la pendiente de la línea es\(K_m/V_{max}\).
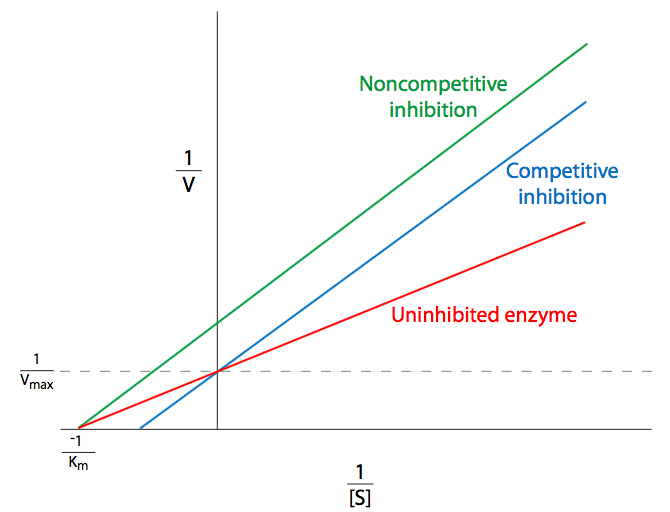
La trama Lineweaver-Burk
Obtener\(V_{max}\) y\(K_m\) a partir de una gráfica directa de v contra [S] puede ser difícil porque incluso a concentraciones de sustrato muy altas, los datos experimentales aún pueden estar significativamente por debajo del\(V_{max}\). Esto lleva a una subestimación de la V máx.
La trama Lineweaver-Burk aborda esta preocupación, pero tiene algunas carencias propias. Debido a que es más fácil obtener datos a altas concentraciones, la mayoría de los puntos de datos están cerca de 0, y hay menos puntos de datos disponibles más adelante (a la derecha de la gráfica). Debido a que estos son recíprocos, bajo estas condiciones bajas [S], pequeños errores en los valores medidos de se\(v\) convierten en grandes errores en 1/ v, y por lo tanto grandes errores en\(K_M\) y V máx. Esto es evidente al examinar la ecuación Lineweaver-Burk:
\[\frac { 1 } { v } = \left( \frac { K _ { M } } { V _ { \max } } \right) \frac { 1 } { [ S ] } + \frac { 1 } { V _ { \max } }\]


