4.2: Permeabilidad de membrana

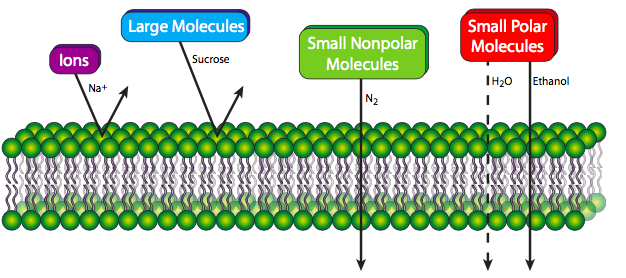
Una bicapa fosfolipídica pura, cualquiera que sea la composición lipídica, es una membrana semipermeable que generalmente es repelente a moléculas grandes y a iones. Las moléculas polares pequeñas a veces pueden pasar fácilmente (por ejemplo, etanol), pero más a menudo pasan a tasas bajas, si es que lo hacen (por ejemplo, agua). Sin embargo, pequeñas moléculas no polares son capaces de pasar a través de la membrana con relativa facilidad. Las razones deben ser evidentes: las moléculas más grandes simplemente no pueden encajar entre las moléculas lipídicas para abrirse paso. Las moléculas pequeñas que puedan caber deben ser hidrófobas, de lo contrario el núcleo de acilo graso de la membrana los repelerá y los bloqueará para que no procedan. Las concentraciones más altas de colesterol, al rellenar huecos entre las colas de fosfolípidos, disminuyen la permeabilidad incluso para moléculas pequeñas que normalmente pueden pasar a través de la membrana fácilmente. Las células necesitan mucho más que pequeñas moléculas no polares para sus necesidades de material y energía. Afortunadamente para la vida en la Tierra, las membranas de las células vivas no son puramente fosfolípidos, y como veremos, las proteínas incrustadas en la bicapa de fosfolípidos pueden formar medios de transporte para el transporte de muchas moléculas diferentes dentro y fuera de la membrana.

Figura\(\PageIndex{7}\). Una bicapa fosfolipídica pura es inherentemente semipermeable.

De hecho, la observación de la cinética de saturación en el transporte de glucosa en membranas de eritrocitos fue la primera indicación de transporte mediado por proteínas (el transportador de glucosa GLUT ₁). Otra observación reveladora fue el hallazgo de que la permeabilidad a la glucosa a través de las membranas de eritrocitos es un millón de veces mayor que la de una bicapa lipídica artificial La concentración de glucosa en la sangre es relativamente alta en comparación con la del interior de la mayoría de las células, por lo que este es el transporte mediado, pero el transporte pasivo ya que va bajando el gradiente de concentración. Para facilitar el proceso evitando una acumulación de concentración de glucosa en la célula, el primer paso del metabolismo de la glucosa es la fosforilación para convertirla en una molécula diferente, glucosa-6-fosfato. Así la concentración de glucosa se mantiene muy baja, y fluye fácilmente desde el torrente sanguíneo hacia la célula.

Existen algunas diferencias obvias entre el transporte de moléculas directamente a través de la bicapa lipídica (transporte no mediado) y el transporte usando un facilitador de proteínas embebido en la membrana (transporte mediado). El transporte no mediado se rige por la difusión: el soluto se mueve de áreas de alta concentración a áreas de baja concentración, eliminando así el gradiente. Mientras un soluto (A) pueda atravesar la membrana, su flujo (J) está determinado únicamente por la diferencia de concentración y la permeabilidad (P) de la membrana: J _{A = P A} ([_A] _out - [A] _in) y la relación entre el ux a través de la membrana y el el diferencial de concentración es lineal.

Este no es el caso en el transporte mediado. Como su nombre lo indica, se requiere un intermediario proteico, y las campanas de alarma deberían estar sonando en tu cabeza diciendo, “hay un límite”, a la cantidad de proteínas de transporte disponibles en un momento dado. Por lo tanto, tal como vimos con la cinética enzimática en el capítulo 3, la ux de solutos que pasan por un transportador no está relacionada linealmente con el diferencial de concentración a través de la membrana, aunque todavía hay un efecto de concentración. En cambio, la relación es logarítmica, alcanzando una meseta de saturación una vez que todas las proteínas de transporte disponibles están en uso. En ese punto, aumentar la concentración del soluto no aumentará su flujo a través de la membrana. Así, para el transporte mediado unidireccional simple de un soluto (\(B\)\(J\)), el flujo () puede expresarse como un valor de la afinidad del transportador por el soluto (\(K_M\)) y la concentración del soluto:

\[J_B = \dfrac{J_{max}[B]}{K_M + [B]}\]

La permeabilidad de la membrana permite la posibilidad de gradientes de concentración a través de las membranas, que a su vez tienen energía potencial asociada con la concentración diferencial a través de la membrana. Esto resulta ser una fuente fenomenalmente importante de energía celular, y es la base para la síntesis aeróbica de ATP por fosforilación oxidativa (capítulo 5). Sin embargo, para tener una discusión significativa sobre cómo las diferencias de concentración entre membranas semipermeables almacenan energía, debemos revisar algunos conceptos básicos primero.

Si una fuente puntual (por ejemplo, una “glob”) de un soluto (por ejemplo, miel) se coloca en un disolvente (por ejemplo, té), comienza a disolverse y, a medida que lo hace, la concentración de soluto cerca de la fuente puntual comenzará mucho más alta que la concentración hacia la periferia del recipiente (por ejemplo, taza de té). Con el tiempo, el soluto luego se difunde desde la fuente puntual hacia afuera en todas las direcciones disponibles, y eventualmente la concentración de soluto es igual en cualquier punto en el espacio de la taza del té. Este comportamiento se rige por la Segunda Ley de la Termodinámica. El soluto se concentra inicialmente, lo que significa que sus moléculas constituyentes están relativamente orga-nizadas. Por la segunda ley, estas moléculas tenderán al caos, alejándose de las limitaciones del punto inicial hacia un área con concentraciones más bajas del soluto.

Ahora, imagina un muro temporal alrededor de la fuente puntual. La tendencia natural es que los solutos se dispersen, por lo que al impedir ese movimiento, se ha embotellado alguna energía potencial. Por supuesto, esto es solo energía potencial si existe alguna posibilidad de que los solutos eventualmente puedan atravesar la barrera (por ejemplo, la pared tiene ventanas que se pueden abrir). Si los solutos tienen absolutamente cero posibilidades de pasar, entonces no hay energía potencial porque no hay potencial para salir de ahí. Recordando el capítulo Energía en el que se introdujo la segunda ley, la energía potencial química de un soluto es

\[G=RT \ln[A]+G^\prime\]

por lo que la diferencia de potencial químico a través de una membrana es entonces

\[ΔG= RT \ln \left(\dfrac{[A_i]}{[A_o]}\right).\]

Ahora imagínese esto como algo así como una presa hidroeléctrica, donde hay una gran cantidad de presión acumulándose detrás de la presa, que puede ser utilizada cuando se permite el paso de parte del agua, alimentando turbinas que generan electricidad. En el caso biológico, hay presión de concentración acumulándose tanto dentro como fuera de la célula debido a que la tendencia termodinámica natural es llevar las concentraciones internas y externas de cada soluto al equilibrio. Cuando esta presión se libera permitiendo que los iones u otras moléculas pasen a través de la membrana, se libera energía, y puede ser capturada y utilizada. El ejemplo más directo de esto es la ATP sintasa impulsada por gradiente de protones en la membrana mitocondrial interna (Capítulo 5), que contiene un equivalente molecular directo al giro de una rueda hidráulica con el ow de agua. Para otro ejemplo, si observamos [Na ⁺] en una célula animal, la concentración extracelular es mucho mayor que la intracelularmente. Cuando se abre un canal de Na ⁺, los iones Na ⁺ se precipitan hacia adentro para tratar de igualar la concentración de Na ⁺ dentro y fuera de la célula. El equilibrio no se alcanza realmente en una célula viva porque los canales de Na ⁺ están estrechamente regulados y solo se abren por cortos periodos de tiempo.

En las células, los gradientes de concentración de iones son grandes fuentes de energía porque la parte lipídica de la membrana es fuertemente repelente a los iones, impidiendo que pasen a través de ellos, pero la membrana está incrustada con canales y transportadores que pueden permitir que los iones pasen si y cuando están abiertos. Debido a que los iones tienen tanto diferenciales de concentración como diferenciales de carga a través de la membrana, la diferencia de potencial electroquímico a través de la membrana está representada por una modificación de la ecuación de diferencia de potencial químico con un término que toma en cuenta esa carga eléctrica:

\[ΔG=RT \ln \left( \dfrac{[A_i]}{[A_o]}\right) + ZFΔΨ\]

Z es la carga del ion (por ejemplo +1 para Na ⁺, -1 para Cl ^-, +2 para Ca ²⁺), F es la constante de Faraday (9.6485 x 10 ⁵ C/mol) y Δψ es el potencial de membrana. En una célula animal promedio, el potencial de membrana es aproximadamente -70mV. El número es negativo para mostrar que el interior de la celda es negativo con respecto al exterior. Así, nuevamente considerando Na ⁺, no solo hay un gradiente químico de más iones Na ⁺ fuera de la célula que dentro, también hay un gradiente de carga de cargas más positivas fuera de la célula hacia adentro, por lo que ambas fuerzas contribuyen a que la energía de Na ⁺ fluya hacia la célula. El potencial de equilibrio de un ion (por ejemplo, Na ⁺) a través de una membrana está determinado por la ecuación de Nernst:

\[E_m= \left(\dfrac{RT}{zF}\right) \ln \left(\dfrac{[Na^+]_{out}}{[Na^{+}]_{in}}\right)\]

que se extiende en la ecuación de Goldman (también ecuación de Goldman-Hodgkin-Katz) que calcula el potencial de membrana basado en múltiples gradientes de iones. Para la mayoría de las células animáticas, se puede calcular una buena aproximación del potencial general de membrana usando los tres gradientes principales: Na+, K+ y Cl-. Hay, por supuesto, otros gradientes iónicos, pero sus contribuciones son normalmente mucho menores que estos tres.

El potencial de membrana es relativamente estable en células no excitables, pero en neuronas y células musculares, el potencial de membrana es bastante dinámico, por lo que el potencial de membrana en estado no excitado se denomina en estas células como el potencial de reposo. El potencial de membrana (reposo) en la mayoría de las células animales es de alrededor de -70mV. Esto se debe en gran parte a la presencia de canales de fuga K ⁺. Estos canales filtran K ⁺ de la célula por el gradiente de concentración hasta que la diferencia de potencial químico de K+ está en equilibrio con el potencial de membrana. En otras palabras, el gradiente que empuja K ⁺ hacia fuera eventualmente será detenido por una fuerza igual del gradiente empujando iones positivos (incluyendo K ⁺) de nuevo hacia adentro. También hay canales de fuga de Na ⁺ y Cl ^-, pero hay muchos menos y contribuyen mucho menos al potencial de reposo que K ⁺.

Los canales de fuga de potasio son estructuralmente y funcionalmente diferentes de otros canales de potasio. Donde la mayoría de los canales K ⁺ tienen un dominio de poro, los canales de fuga tienen dos. Si bien los canales de fuga, por definición, no están controlados por voltaje, ni apreciablemente activados o inactivados, esto no es cierto para todos los miembros de la familia de canales de potasio de dominio de poro en tándem. Curiosamente, algunos (por ejemplo TASK-1) son mecanorreceptores, que se abren en respuesta al estiramiento de la membrana, y otros actúan como termoreceptores, con activación sensible al calor (por ejemplo, TREK-1).

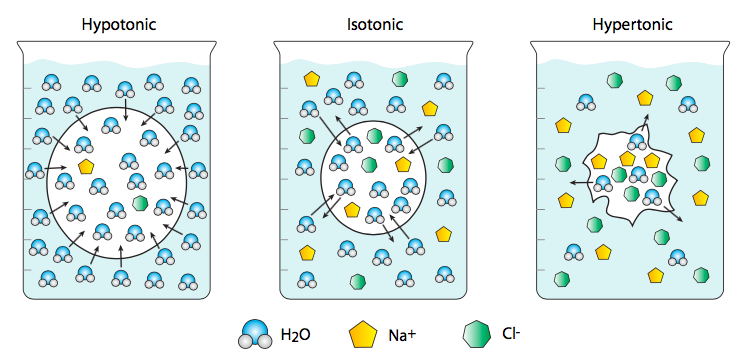
Aunque comúnmente pensamos en el agua como el disolvente en el que se difunden moléculas “interesantes” (por ejemplo, iones), su concentración y movimiento a través de las membranas tiene importantes consecuencias biológicas. La ósmosis es un término que se refiere específicamente a la difusión del agua a través de una membrana. En este caso, el agua se considera un soluto en lugar de un disolvente, de manera que si un liposomas permeante al agua, embebido con canales de acuaporina para permitir el paso del agua, se coloca en una solución salina muy salada, la celda se encogerá debido a que hay una menor proporción de agua a sales disueltas fuera de la célula. que en el interior. Esta es una solución hipertónica relativa a la célula. Por lo tanto, el agua fluye desde la celda (mayor concentración de agua) hacia la solución salina (con menor concentración de agua). Por el contrario, una célula colocada en agua destilada y desionizada se hinchará y potencialmente estallará porque el agua se precipita de la mayor concentración posible (agua pura) a un citoplasma con menor concentración de agua (porque disueltos en ella se encuentran diversos iones y otras moléculas). Este es un ejemplo de una solución hipotónica. Una solución isotónica tendrá la misma concentración de agua dentro y fuera de la célula.

Figura\(\PageIndex{8}\). Osmosis. Una “célula” artificial que es permeable al agua pero no a Na ⁺, K ⁺ o Cl ^- se coloca en una solución acuosa de salinidad variable.