3.2: Introducción
- Page ID
- 54253
En el capítulo anterior, utilizamos programación dinámica para calcular alineaciones de secuencias en\(O(n^2)\). En particular, aprendimos el algoritmo de alineación global, que empareja secuencias completas entre sí a nivel de nucleótidos. Normalmente aplicamos esto cuando se sabe que las secuencias son homólogas (es decir, las secuencias provienen de organismos que comparten un ancestro común).
La importancia biológica de encontrar alineamientos de secuencias es poder inferir el conjunto más probable de eventos evolutivos como mutaciones puntuales/desapareamientos y huecos (inserciones o deleciones) que ocurrieron para transformar una secuencia en otra. Para ello, primero asumimos que el conjunto de transformaciones con el menor costo es la secuencia de transformaciones más probable. Al asignar costos a cada tipo de transformación (desajuste o brecha) que reflejen sus respectivos niveles de dificultad evolutiva, encontrar una alineación óptima se reduce a encontrar el conjunto de transformaciones que dan como resultado el menor costo general.
Esto lo conseguimos usando un algoritmo de programación dinámica conocido como el algoritmo Needleman-Wunsch. La programación dinámica utiliza subestructuras óptimas para descomponer un problema en subproblemas similares. El problema de encontrar una alineación de secuencias se puede expresar muy bien como un algoritmo de programación dinámica ya que las puntuaciones de alineación son aditivas, lo que significa que encontrar el alineamiento de una secuencia más grande se puede encontrar encontrando recursivamente las alineaciones de subsecuencias más pequeñas. Las puntuaciones se almacenan en una matriz, con una secuencia correspondiente a las columnas y la otra secuencia correspondiente a las filas. Cada célula representa la transformación requerida entre dos nucleótidos correspondientes a la fila y columna de la célula. Se recupera una alineación trazando de nuevo a través de la matriz de programación dinámica (que se muestra a continuación). El enfoque de programación dinámica es preferible a un algoritmo codicioso que simplemente elige la transición con un costo mínimo en cada paso porque un algoritmo codicioso no garantiza que el resultado general dará la alineación óptima o de menor costo.
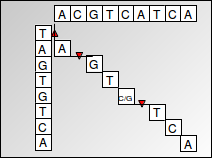
Figura 3.1: Alineación global
Para resumir el algoritmo de Needleman-Wunsch para la alineación global:
Calculamos las puntuaciones correspondientes a cada celda de la matriz y registramos nuestra elección (memorización) en ese paso, es decir, cuál de las celdas superior, izquierda o diagonal condujo a la puntuación máxima para la celda actual. Nos quedamos con una matriz llena de puntuaciones óptimas en cada posición de celda, junto con punteros en cada celda que reflejan la elección óptima que conduce a esa celda en particular.
Luego podemos recuperar la alineación óptima trazando desde la celda en la esquina inferior derecha (que contiene la puntuación de alinear una secuencia completa con la otra) siguiendo los punteros que reflejan elecciones localmente óptimas, y luego construyendo la alineación correspondiente a una ruta óptima seguida en la matriz.
El tiempo de ejecución del algoritmo Needleman-Wunsch es O (n2) ya que para cada celda de la matriz, hacemos una cantidad finita de cálculo. Calculamos 3 valores usando puntuaciones ya calculadas y luego tomamos el máximo de esos valores para encontrar la puntuación correspondiente a esa celda, que es una operación de tiempo constante (O (1)).
Para garantizar la corrección, es necesario computar el costo para cada celda de la matriz. Es posible que la alineación óptima pueda estar compuesta por una mala alineación (consistente en brechas y desajustes) al inicio, seguida de muchos partidos, convirtiéndola en la mejor alineación general. Estos son los casos que atraviesan el límite de nuestra matriz de alineación. Así, para garantizar la óptima alineación global, necesitamos computar cada entrada de la matriz.
El alineamiento global es útil para comparar dos secuencias que se cree que son homólogas. Es menos útil para comparar secuencias con reordenamientos o inversiones o alinear un gen recién secuenciado contra genes de referencia en un genoma conocido, conocido como búsqueda en bases de datos. En la práctica, a menudo también podemos restringir el espacio de alineación a explorar si sabemos que algunas alineaciones son claramente subóptimas.
En este capítulo se abordarán otras formas de algoritmos de alineación para abordar tales escenarios. Primero introducirá el algoritmo de Smith-Waterman para el alineamiento local para alinear subsecuencias en lugar de secuencias completas, en contraste con el algoritmo de Needleman-Wunsch para alineación global. Más adelante, se dará una visión general de los métodos hash y semi-numéricos como el algoritmo de Karp-Rabin para encontrar la subcadena común más larga (contigua) de nucleótidos. Estos algoritmos son implementados y ampliados para emparejamientos inexactos en el programa BLAST, una de las herramientas más citadas y exitosas en biología computacional. Finalmente, este capítulo repasará BLAST para la búsqueda de bases de datos, así como la base probabilística del alineamiento de secuencias y cómo las puntuaciones de alineación pueden interpretarse como razones de verosimilitud.
Esquema:
- Introducción
• Revisión del alineamiento global (Needleman-Wunsch)
- Alineación global vs. alineación local vs. alineación semi-global
- Reglas de inicialización, terminación y actualización para alineación global (Needleman-Wunsch) vs. alineación local (Smith-Waterman) vs. alineación semi-global
- Penalizaciones por brecha variable, aceleraciones algorítmicas
- Coincidencia exacta de cadenas en tiempo lineal
• Algoritmo Karp-Rabin y métodos semi-numéricos • Funciones hash y algoritmos aleatorios
- El algoritmo BLAST y coincidencia inexacta • Hashing con búsqueda de vecindarios
• Explosión de dos golpes y hash con peines
- Preprocesamiento para la coincidencia de cadenas en tiempo lineal
• Preprocesamiento fundamental
• Árboles de sufijos
• Matrices de sufijos
• Transformación de Madrias-Wheeler - Fundamentos probabilísticos del alineamiento de secuencias • Penalizaciones por desajuste, matrices BLOSUM y
• Significancia estadística de una puntuación de alineación


