3.6: Preprocesamiento para la coincidencia de cadenas en tiempo lineal
- Page ID
- 54273
La técnica de hash en el núcleo del algoritmo BLAST es una poderosa forma de cadena para una búsqueda rápida. Se invierte un tiempo sustancial para procesar todo el genoma, o un gran conjunto de genomas, antes de obtener una secuencia de consulta. Una vez obtenida la secuencia de consulta, se puede procesar de manera similar y sus partes se pueden buscar en la base de datos indexada en tiempo lineal.
En esta sección, describimos brevemente cuatro formas adicionales de preprocesar una base de datos para una búsqueda rápida de cadenas, cada una de las cuales tiene importancia práctica y teórica.
Árboles de sufijos
Los árboles de sufijos proporcionan una poderosa representación de árboles de subcadenas de una secuencia diana T, capturando todos los sufijos de T en un árbol de base.
Representación de una secuencia en un árbol de sufijos
Buscar una nueva secuencia contra un árbol de sufijos
Construcción lineal de árboles de sufijos
Matrices de sufijos
Para muchas aplicaciones genómicas, los árboles de sufijos son demasiado caros de almacenar en la memoria, y se necesitaron repeticiones más eficientes. Las matrices de sufijos se desarrollaron específicamente para reducir el consumo de memoria de los árboles de sufijos y lograr los mismos objetivos con una necesidad de espacio significativamente reducida.
Usando matrices de sufijos, cualquier subcadena se puede encontrar haciendo una búsqueda binaria en la lista ordenada de sufijos. Al explorar así el prefijo de cada sufijo, terminamos buscando en todas las subcadenas.
La transformación de Madrows-Wheeler
Una representación aún más eficiente que los árboles de sufijos viene dada por la transformada de Burrows-Wheeler (BWT), que permite almacenar toda la cadena hash en el mismo número de caracteres que la cadena original (e incluso de manera más compacta, ya que contiene series frecuentes de homopolímeros de caracteres que pueden ser más fáciles comprimida). Esto ha ayudado a hacer programas que pueden funcionar de manera aún más eficiente.
Primero consideramos la matriz BWT, que es una extensión de una matriz de sufijos, ya que contiene no solo todos los sufijos en orden ordenado (lexicográfico), sino que añade a cada sufijo comenzando en la posición i el prefijo que termina en la posición i − 1, conteniendo así cada fila una rotación completa de la cadena original. Esto permite todas las operaciones de matriz de sufijos y árbol de sufijos, de encontrar la posición de los sufijos en el tiempo lineal en la cadena de consulta.
La diferencia clave con las matrices de sufijos es el uso del espacio, donde en lugar de almacenar todos los sufijos en la memoria, lo que incluso para matrices de sufijos es muy costoso, solo se almacena la última columna de la matriz BWT, en base a la cual se puede recuperar la matriz original.
Una matriz auxiliar se puede utilizar para acelerar aún más las cosas y evitar tener que repetir operaciones de encontrar la primera aparición de cada carácter en la matriz de sufijos modificada.
Por último, una vez que se encuentran las posiciones de 100.000s de subcadenas en la cadena modificada (la última columna de la matriz BTW), estas coordenadas se pueden transformar a las posiciones originales, ahorrando tiempo de ejecución al amortizar el costo de la transformación a través de las muchas lecturas.
El BWT ha tenido un impacto muy fuerte en los algoritmos de coincidencia de cadenas cortas, y casi todos los mapeadores de lectura más rápida se basan actualmente en la transformación Burrows-Wheeler.
Pre-procesamiento fundamental
Esta es una variación del procesamiento que tiene interés teórico pero que ha encontrado relativamente poco uso práctico en bioinformática. Se basa en el vector Z, que contiene en cada posición i la longitud del prefijo más largo de una cadena que también coincide con la subcadena comenzando en i. Esto permite calcular los vectores L y R (Izquierda y Derecha) que denotan el final de las subcadenas duplicadas más largas que contienen la posición actual i.
Coincidencia de cuerdas educadas
El algoritmo Z permite un cálculo sencillo de los algoritmos Boyer-Moore y Knuth-Morris-Pratt para la coincidencia de cadenas en tiempo lineal. Estos algoritmos utilizan la información recopilada en cada comparación al hacer coincidir cadenas para mejorar la coincidencia de cadenas con O (n). El algoritmo ingenuo es el siguiente: compara su cadena de longitud m carácter por carácter con la secuencia. Después de comparar toda la cadena, si hay algún desajuste, se mueve al siguiente índice y vuelve a intentarlo. Esto se completa en\( O(m ∗ n) \) el tiempo.
Una mejora de este algoritmo es descontinuar la comparación actual si se encuentra un desajuste. Sin embargo, esto todavía se completa en el\( O(m ∗ n) \) tiempo cuando la cadena que estamos comparando coincide con la secuencia completa.
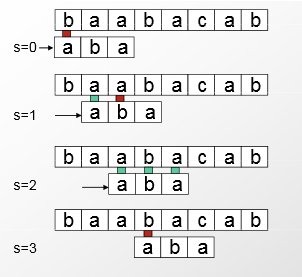
La visión clave proviene de aprender de la redundancia interna en la cadena para comparar, y usarlo para hacer cambios más grandes hacia abajo en la secuencia objetivo. Cuando se comete un error, todas las bases en la comparación actual se pueden utilizar para mover el fotograma considerado para la siguiente comparación más abajo. Como se ve a continuación, esto reduce en gran medida el número de comparaciones requeridas, disminuyendo el tiempo de ejecución a\( O(n) \).

© fuente desconocida. Todos los derechos reservados. Este contenido está excluido de nuestra licencia Creative Commons. Para obtener más información, consulte http://ocw.mit.edu/help/faq-fair-use/.


