3.7: Fundamentos probabilísticos del alineamiento de secuencias
- Page ID
- 54252
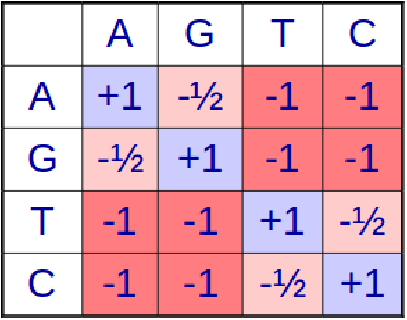
Como se describió anteriormente, el algoritmo BLAST utiliza una matriz de puntuación (sustitución) para expandir la lista de W-meros con el fin de buscar y determinar una secuencia aproximadamente coincidente durante la extensión de la semilla. Además, se utiliza una matriz de puntuación en la evaluación de coincidencias o desajustes en los algoritmos de alineación. Pero, ¿cómo construimos esta matriz en primer lugar? ¿Cómo se determina el valor de\( s\left(x_{i}, y_{j}\right) \) en alineación global/local?
La idea detrás de la matriz de puntuación es que la puntuación de alineación debe reflejar la probabilidad de que dos secuencias similares sean homólogas, es decir, la probabilidad de que dos secuencias que tienen un montón de nucleótidos en común también compartan una ascendencia común. Para ello, nos fijamos en los cocientes de verosimilitud entre dos hipótesis.
1. Hipótesis 1: — Que el alineamiento entre las dos secuencias se debe al azar y las secuencias son, de hecho, no relacionadas.
2. Hipótesis 2: — Que el alineamiento se debe a la ascendencia común y las secuencias están realmente relacionadas.
Luego, calculamos la probabilidad de observar una alineación de acuerdo a cada hipótesis. Pr (x, y|u) es la probabilidad de alinear x con y asumiendo que no están relacionados, mientras que Pr (x, y|R) es la probabilidad de la
alineación, suponiendo que estén relacionados. Luego, definimos la puntuación de alineación como el log de la relación de verosimilitud entre los dos:
\ [\ begin {ecuación}
S\ equiv\ log\ frac {P (\ mathbf {x},\ mathbf {y}\ mid R)} {P (\ mathbf {x},\ mathbf {y}\ mid U)}
\ end {ecuación}\ nonumber\]
Dado que una suma de registros es un registro de productos, podemos obtener la puntuación total de la alineación sumando las puntuaciones de las alineaciones individuales. Esto nos da la probabilidad de toda la alineación, asumiendo que cada alineación individual es independiente. Así, una puntuación de matriz aditiva nos da exactamente la probabilidad de que las dos secuencias estén relacionadas, y el alineamiento no se debe al azar. De manera más formal, considerando el caso de alinear proteínas, para secuencias no relacionadas, la probabilidad de tener un alineamiento de n residuos entre x e y es un producto simple de las probabilidades de las secuencias individuales ya que los emparejamientos de residuos son independientes.
Es decir,
\ [\ comenzar {ecuación}
\ comenzar {alineado}
\ mathbf {x} &=\ izquierda\ {x_ {1}\ lpuntos x_ {n}\ derecha\}\
\ mathbf {y} &=\ izquierda\ {y_ {1}\ lpuntos x_ {n}\ derecha\}\
q_ {a} &=P (\ texto {aminoácido} a)\
P (\ mathbf {x},\ mathbf {y}\ media U) &=\ prod_ {i=1} ^ {n} q_ {x_ {i}}\ prod_ {i=1} ^ {n} q_ {y_ {i}}
\ end {alineado}
\ end {ecuación}\ nonumber\]
Para secuencias relacionadas, los emparejamientos de residuos ya no son independientes por lo que debemos usar una articulación diferente
probabilidad, suponiendo que cada par de aminoácidos alineados evolucionó a partir de un ancestro común:
\ [\ begin {ecuación}
\ begin {alineado}
p_ {a b} &=P (\ text {evolución dio lugar a} a\ text {in}\ mathbf {x}\ text {y} b\ text {in}\ mathbf {y})\\
P (\ mathbf {x},\ mathbf {y}\ mid R) &=\ prod_ {i=1} ^ {n} p_ {x_ {i} y_ {i}}
\ fin {alineado}
\ end {ecuación}\ nonumber\]
Entonces, la razón de verosimilitud entre los dos viene dada por:
\ [\ begin {ecuación}
\ begin {alineado}
\ frac {P (\ mathbf {x},\ mathbf {y}\ mid R)} {P (\ mathbf {x},\ mathbf {y}\ mid U)} &=\ frac {\ prod_ {i=1} ^ {n} p_ {x_ {i} y_ {i}} {\ prod_ {i=1} ^ {n} q_ {x_ {i}}\ prod_ {i=1} ^ {n} q_ {y_ {i}}}\\
&=\ frac {\ prod_ {i=1} ^ {n} p_ {x_ {i} y_ {i}}} {\ prod_ {i=1} ^ {n } q_ {x_ {i}} q_ {y_ {i}}}
\ final {alineado}
\ final {ecuación}\ nonumber\]
Como finalmente queremos calcular una suma de puntajes y probabilidades requieren agregar productos, tomamos el registro del producto para obtener una suma útil:
\ [\ begin {ecuación}
\ begin {alineado}
S &\ equiv\ log\ frac {P (\ mathbf {x},\ mathbf {y}\ mid R)} {P (\ mathbf {x},\ mathbf {y}\ mid U)}\\
v &=\ sum_ {i}\ log\ left (\ frac {p_ {x_ {i} y_ {i}}} {q_ {x_ {i}} q_ {y_ {i}}\ derecha)\\
&\ equiv\ suma_ {i} s\ izquierda (x_ {i}, y_ { i}\ derecha)
\ final {alineado}
\ final {ecuación}\ nonumber\]
Así, la puntuación de la matriz de sustitución para un par dado a, b es dada por
\ [\ begin {ecuación}
s (a, b) =\ log\ left (\ frac {p_ {a b}} {q_ {a} q_ {b}}\ derecha)
\ end {ecuación}\ nonumber\]
La expresión anterior se usa entonces para producir una matriz de sustitución como el BLOSUM62 para aminoácidos. Es interesante señalar que la puntuación de una coincidencia de un aminoácido consigo mismo depende del aminoácido en sí mismo porque la frecuencia de ocurrencia aleatoria de un aminoácido afecta los términos utilizados en el cálculo de la puntuación de la relación de verosimilitud de alineación. De ahí que estas matrices capturen no sólo la similitud de secuencia de los alineamientos, sino también la similitud química de diversos aminoácidos.
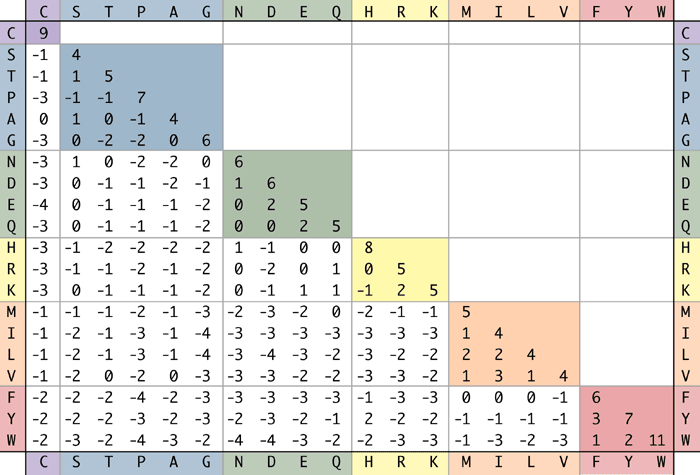
Figura 3.17: Matriz BLOSUM62 para aminoácidos
Lectura adicional:
Algoritmos relacionados con BLAST: Califino-Rigoutsos'93, Buhler'01 e Indyk-Motwani'98


