7.3: Cadenas de Markov y HMMS - Del ejemplo a la formalización
- Page ID
- 54335
Ejemplo Motivador: Predicción del Tiempo
La predicción del tiempo siempre ha sido difícil, sobre todo cuando nos gustaría pronosticar el clima muchos días, semanas o incluso meses después. Sin embargo, si solo necesitamos predecir el clima del día siguiente, podemos alcanzar una precisión de predicción decente usando algunos modelos bastante simples como Markov Chain y Hidden Markov Model construyendo modelos gráficos en la Figura 7.2.
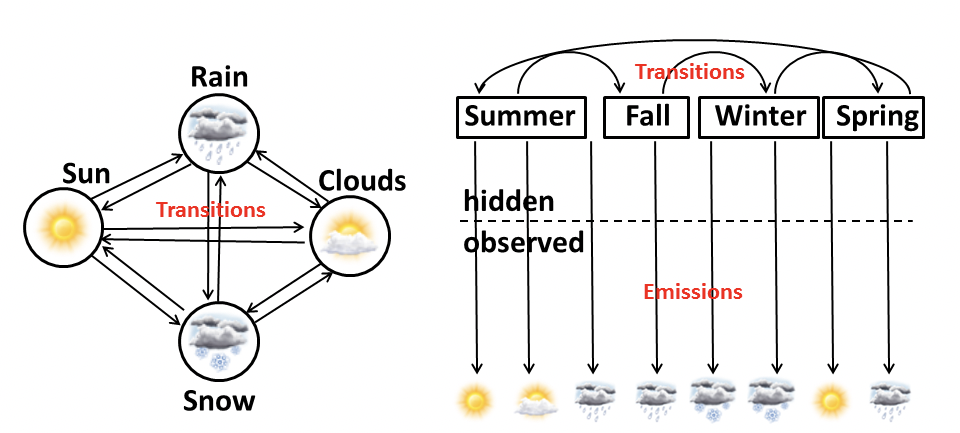
Para el modelo Markov Chain de la izquierda, cuatro tipos de clima (Sol, Lluvia, Nubes y Nieve) pueden pasar directamente de uno a otro. Esto es un “lo que ves es lo que obtienes” en que el siguiente estado sólo depende del estado actual y no hay memoria del estado anterior. Sin embargo para HMM a la derecha, todos los tipos de clima se modelan como la emisión (o resultado) de las estaciones ocultas (Verano, Otoño, Invierno y Primavera). La visión clave detrás es que los estados ocultos del mundo (por ejemplo, estación o sistema de tormentas) determinan las probabilidades de emisión mientras que las transiciones de estado están gobernadas por una cadena de Markov.
Formalización de la Cadena de Markov y HMMS
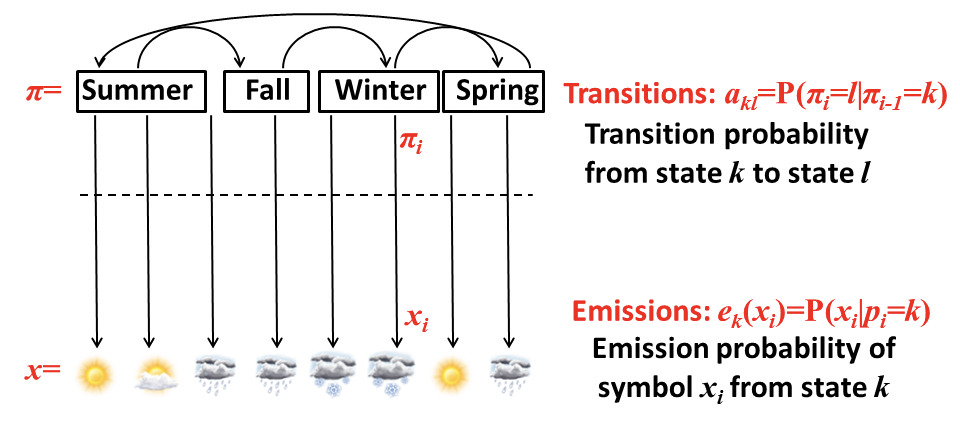
Para echar un vistazo más de cerca al modelo Hidden Markov, primero definamos los parámetros clave en la Figura 7.3. El vector x representa la secuencia de observaciones. El vector π representa la ruta oculta, que es la secuencia de estados ocultos. Cada entrada a kl de la matriz de transición A denota la probabilidad de transición del estado k al estado l. Cada entrada e k (x i) del vector de emisión denota la probabilidad de observar x i desde el estado k. Y finalmente con estos parámetros y la regla de Bayes, podemos usar p (x i |π i = k) para estimar p (π i = k|x i).
Cadenas Markov
Una Cadena de Markov viene dada por un conjunto finito de estados y probabilidades de transición entre los estados. En cada paso de tiempo, la Cadena Markov se encuentra en un estado particular y experimenta una transición a otro estado. La probabilidad de transición a otro estado depende únicamente del estado actual, y en particular es independiente de cómo se alcanzó el estado actual. Más formalmente, una Cadena de Markov es un triplete (Q, p, A) que consiste en:
Un conjunto de estados Q.
- Una matriz de transición A cuyos elementos corresponden a la probabilidad Aij de transición del estado i al estado j.
- Un vector p de probabilidades de estado inicial.
La propiedad clave de las Cadenas de Markov es que no tienen memoria, es decir, cada estado depende únicamente del estado anterior. Entonces podemos definir inmediatamente una probabilidad para el siguiente estado, dado el estado actual:
\[P\left(x_{i} \mid x_{i-1}, \ldots, x_{1}\right)=P\left(x_{i} \mid x _{i-1}\right)\]
De esta manera, la probabilidad de la secuencia se puede descomponer de la siguiente manera:
\[P (x) = P (x_L, x_{L−1}, ..., x_1) = P (x_L|x_{L−1})P (x_{L−1}|x_{L−2})...P (x_2|x_1)P (x_1)\]
\(P(xL)\)también se puede calcular a partir de las probabilidades de transición: Si multiplicamos las probabilidades de estado iniciales en el tiempo t = 0 por la matriz de transición A, obtenemos las probabilidades de los estados en el tiempo t = 1. Multiplicando por la potencia apropiada AL de la matriz de transición, obtenemos las probabilidades de estado en el tiempo t = L.
Modelos ocultos de Markov
Los modelos ocultos de Markov se utilizan como representación de un espacio problemático en el que las observaciones surgen como resultado de estados de un sistema que no podemos observar directamente. Estas observaciones, o emisiones, resultan de un estado particular basado en un conjunto de probabilidades. Así, los HMM son Modelos Markov donde los estados están ocultos al observador y en su lugar tenemos observaciones generadas con ciertas probabilidades asociadas a cada estado. Estas probabilidades de observaciones se conocen como probabilidades de emisión.
Formalmente, un modelo oculto de Markov es una tupla de 5 (Q, A, p, V, E) que consta de los siguientes parámetros:
- Una serie de estados, Q.
- Una matriz de transición, A
- Un vector de probabilidades de estado inicial, p.
- Un conjunto de símbolos de observación, V, por ejemplo {A, T, C, G} o el conjunto de aminoácidos o palabras en un diccionario de inglés.
- Una matriz de probabilidades de emisión, E: Para cada s, t, en Q, la probabilidad de emisión es e sk = P (v k en el tiempo t|q t = s)
La propiedad clave de la falta de memoria se hereda de Markov Models. Las emisiones y transiciones dependen únicamente del estado actual y no de la historia pasada.


