7.5: Ajustes algorítmicos para HMM
- Page ID
- 54280
Utilizamos HMM para tres tipos de operación: puntuación, decodificación y aprendizaje. Hablaremos de puntuación y decodificación en esta conferencia. Estas operaciones pueden ocurrir para una sola ruta o todas las rutas posibles. Para las operaciones de ruta única, nuestro enfoque está en descubrir el camino con la máxima probabilidad. Sin embargo, estamos interesados en una secuencia de observaciones o emisiones para todas las operaciones de ruta independientemente de sus trayectorias correspondientes.
Apuntar
Apuntar en una sola trayectoria
El problema del casino deshonesto y el problema de Predicción de regiones ricas en GC descritos en la sección 7.4 son ejemplos de encontrar la puntuación de probabilidad correspondiente a una sola ruta. Para una sola ruta definimos el problema de puntuación de la siguiente manera:
• Entrada: Una secuencia de observaciones x = x 1 x 2.. x n generada por un HMM M (Q, A, p, V, E) y una ruta de estados π = π 1 π 2... π n.
• Salida: Probabilidad conjunta, P (x, π) de observar x si la secuencia de estado oculto es π.
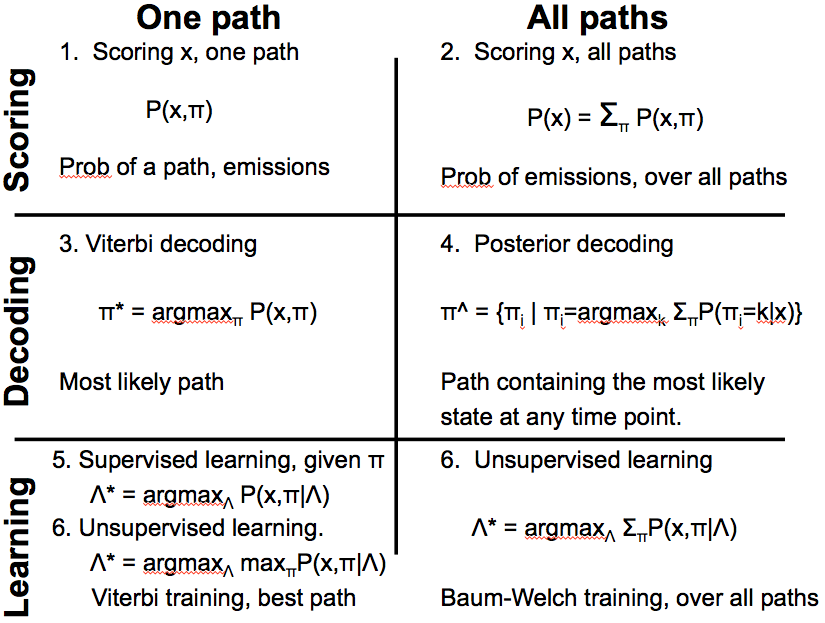
El cálculo de ruta única es esencialmente la probabilidad de observar la secuencia dada sobre una ruta particular usando la siguiente fórmula:
P (x, π) = P (x|π) P (π) Ya
hemos visto los ejemplos de puntuación de ruta única en nuestro Casino Deshonesto y región rica en GC
ejemplos.
Apuntar en todas las rutas
Definimos la versión all paths del problema de puntuación de la siguiente manera:
• Entrada: Una secuencia de observaciones x = x1x2... xn generada por un HMM M (Q, A, p, V, E).
• Salida: La probabilidad conjunta, P (x, π) de observar x sobre todas las secuencias posibles de estados ocultos π.
La probabilidad sobre todos los caminos π de estados ocultos de la secuencia dada de observaciones viene dada por la siguiente fórmula.
\[P(x)=\sum_{\pi} P(x, \pi) \nonumber \]
Utilizamos esta puntuación cuando estamos interesados en conocer la probabilidad de una secuencia particular para un HMM dado. Sin embargo, el cálculo ingenuo de esta suma requiere considerar un número exponencial de caminos posibles. Posteriormente en la conferencia veremos cómo calcular esta cantidad en tiempo polinomial.
7.5.2 Decodificación
La decodificación responde a la pregunta: Dada alguna secuencia observada, ¿qué camino nos da la máxima probabilidad de observar esta secuencia? Formalmente definimos el problema de la siguiente manera:
• Decodificación sobre una sola ruta:
— Entrada: Una secuencia de observaciones x = x 1 x 2... x N generada por un HMM M (Q, A, p, V, E).
— Salida: El camino más probable de los estados,\(\pi^{*}=\pi_{1}^{*} \pi_{2}^{*} \ldots \pi_{N}^{*}\)
• Decodificación en todas las rutas:
— Entrada: Una secuencia de observaciones x = x 1 x 2... x N generada por un HMM M (Q, A, p, V, E).
— Salida: La ruta de los estados,\(\pi^{*}=\pi_{1}^{*} \pi_{2}^{*} \ldots \pi_{N}^{*}\) que contiene el estado más probable en cada punto temporal.
En esta conferencia, veremos únicamente el problema de la decodificación a través de una sola ruta. El problema de la decodificación en todos los caminos se discutirá en la próxima conferencia.
Para el problema de decodificación de ruta única, podemos imaginar un enfoque de fuerza bruta donde calculamos las probabilidades conjuntas de una secuencia de emisión dada y todas las trayectorias posibles y luego seleccionamos la ruta con la probabilidad conjunta máxima. El problema es que hay un número exponencial de caminos y usar tal búsqueda de fuerza bruta para el camino de máxima verosimilitud entre todos los caminos posibles es muy lento y poco práctico. La programación dinámica se puede utilizar para resolver este problema. Formulemos el problema en el enfoque de programación dinámica.
Nos gustaría conocer la secuencia más probable de estados con base en la observación. Como entradas, se nos dan los parámetros del modelo e i (s), las probabilidades de emisión para cada estado, y a ij s, las probabilidades de transición. También se da la secuencia de emisiones x. El objetivo es encontrar la secuencia de estados ocultos, π ∗, que maximice la probabilidad conjunta con la secuencia dada de emisiones. Es decir,
\(\pi^{*}=\arg \max _{\pi} P(x, \pi) \nonumber\)
Dada la secuencia emitida x podemos evaluar cualquier ruta a través de estados ocultos. No obstante, estamos buscando el mejor camino. Comenzamos por buscar la subestructura óptima de este problema.
Para un mejor camino, podemos decir que, el mejor camino a través de un estado dado debe contener dentro de él lo siguiente: • El mejor camino al estado anterior
• La mejor transición del estado anterior a este estado
• El mejor camino al estado final
Por lo tanto, el mejor camino se puede obtener en base al mejor camino de los estados anteriores, es decir, podemos encontrar una recurrencia para el mejor camino. El algoritmo Viterbi es un algoritmo de programación dinámica que se utiliza comúnmente para obtener la mejor ruta.
Ruta de estado más probable: el algoritmo de Viterbi
Supongamos que v k (i) es la probabilidad conocida de que la ruta más probable termine en la posición (o instancia de tiempo) i en el estado k para cada k Entonces podemos calcular las probabilidades correspondientes en el tiempo i + 1 mediante la siguiente recurrencia.
\[ v_{l}(i+1)=e_{l}\left(x_{i+1}\right) \max _{k}\left(a_{k l} v_{k}(i)\right)\nonumber \]
La ruta más probable π ∗, o la P máxima (x, π), se puede encontrar recursivamente. Suponiendo que conocemos v j (i − 1), la puntuación de la ruta máxima hasta el tiempo i − 1, necesitamos aumentar el cálculo para el siguiente paso de tiempo. La nueva ruta de puntuación máxima para cada estado depende de
• La puntuación máxima de los estados anteriores
• La probabilidad de transición
• La probabilidad de emisión.
En otras palabras, la nueva puntuación máxima para un estado particular en el tiempo i es la que maximiza la transición de todos los estados previos posibles a ese estado particular (la penalización de transición multiplicada por sus puntuaciones previas máximas multiplicadas por la probabilidad de emisión en el momento actual).
Todas las secuencias tienen que comenzar en el estado 0 (el estado de inicio). Al mantener los punteros hacia atrás, la secuencia de estado real se puede encontrar retrocediendo. La solución de este problema de Programación Dinámica es muy similar a los algoritmos de alineación que se presentaron en conferencias anteriores.
A continuación se resumen los pasos del algoritmo Viterbi [2]:
1. Inicialización\( (i=0): v_{0}(0)=1, v_{k}(0)=0 \text { for } k>0\)
2. Recursión\((i=1 \ldots N): v_{k}(i)=e_{k}\left(x_{i}\right) \max _{j}\left(a_{j k} v_{j}(i-1)\right) ; p t r_{i}(l)=\arg \max _{j}\left(a_{j k} v_{j}(i-1)\right)\)
3.Terminación:\(P\left(x, \pi^{*}\right)=\max _{k} v_{k}(N) ; \pi_{N}^{*}=\arg \max _{k} v_{k}(N) \)
4. Traceback\((i=N \ldots 1): \pi_{i-1}^{*}=p t r_{i}\left(\pi_{i}^{*}\right)\)
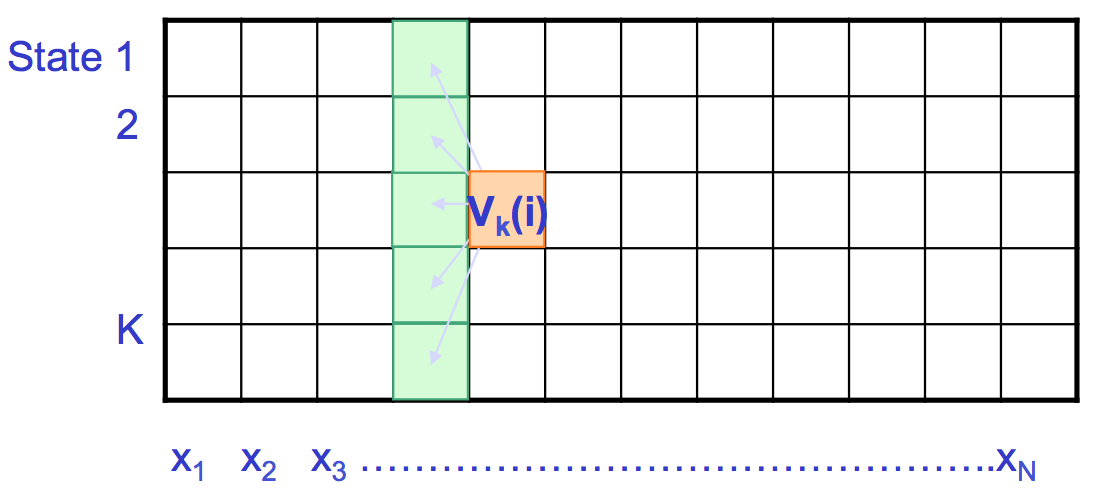
Como podemos ver en la Figura 7.16, llenamos la matriz de izquierda a derecha y trazamos hacia atrás. Cada posición en la matriz tiene K estados a considerar y hay celdas KN en la matriz, por lo que el tiempo de cálculo requerido es O (K 2 N) y el espacio requerido es O (KN) para recordar los punteros. En la práctica, utilizamos puntuaciones logarítmicas para el cálculo. Tenga en cuenta que el tiempo de ejecución se ha reducido de exponencial a polinomio.
Evaluación
La evaluación se trata de responder a la pregunta: ¿Qué tan bien nuestro modelo de los datos capta los datos reales? Dada una secuencia x, muchas rutas pueden generar esta secuencia. La pregunta es ¿qué tan probable es la secuencia dada el modelo? En otras palabras, ¿es este un buen modelo? O bien, ¿qué tan bien captura el modelo las características exactas de una secuencia en particular? Utilizamos la evaluación de HMM para responder a estas preguntas. Adicionalmente, con la evaluación podemos comparar diferentes modelos.
Demos primero una definición formal del problema de Evaluación.
• Entrada: Una secuencia de observaciones x = x 1 x 2... x N y un HMM M (Q, A, p, V, E).
• Salida: La probabilidad de que x fue generada por M sumada en todas las rutas.
Sabemos que si se nos da un HMM podemos generar una secuencia de longitud n usando los siguientes pasos:
• Iniciar en el estado π 1 según la probabilidad a 0π1 (obtenida usando vector, p).
• Emite letra x 1 según probabilidad de emisión e π1 (x 1).
• Ir al estado π 2 según la probabilidad de transición a π1 |π 2
• Siga haciendo esto hasta emitir x N.
Así podemos emitir cualquier secuencia y calcular su verosimilitud. Sin embargo, muchas secuencias de estados pueden emitir la misma x Entonces, ¿cómo calculamos la probabilidad total de generar una x dada sobre todos los caminos? Es decir, nuestro objetivo es obtener la siguiente probabilidad:
\[P(x \mid M)=P(x)=\sum_{\pi} P(x, \pi)=\sum_{\pi} P(x \mid \pi) P(\pi)\nonumber\]
El reto de obtener esta probabilidad es que hay demasiados caminos (un número exponencial) y cada camino tiene una probabilidad asociada. Un enfoque puede ser usar solo el camino de Viterbi e ignorar los demás, ya que ya sabemos cómo obtener este camino. Pero su probabilidad es muy pequeña ya que es sólo uno de los muchos caminos posibles. Es una buena aproximación sólo si tiene alta densidad de probabilidad. En otros casos, el camino Viterbi nos dará una aproximación inexacta. Alternativamente, el enfoque correcto para calcular la suma exacta iterativamente es a través del uso de programación dinámica. El algoritmo que hace esto se conoce como Algoritmo Forward.
El algoritmo Forward
Primero derivamos la fórmula para la probabilidad hacia delante f (i).
\ [\ begin {alineado}
f_ {l} (i) &=P\ izquierda (x_ {1}\ lpuntos x_ {i},\ pi=l\ derecha)\\
&=\ suma_ {\ pi_ {1}\ lpuntos\ pi_ {i-1}} P\ izquierda (x_ {1}\ ldots x_ {i-1},\ pi_ {1},\ ldots,\ pi_ {i-2},\ pi_ {i-1},\ pi_ {i} =l\ derecha) e_ {l}\ izquierda (x_ {i}\ derecha)\\
&=\ suma_ {k}\ suma_ {\ pi_ {1}\ lpuntos\ pi_ {i- 2}} P\ izquierda (x_ {1}\ ldots x_ {i-1},\ pi_ {1},\ ldots,\ pi_ {i-2},\ pi_ {i-1} =k\ derecha) a_ {k l} e_ {l}\ izquierda (x_ {i}\ derecha)\\
&=\ sum_ {k} f_ {k} (i-1) a_ {k l} e_ {l}\ izquierda (x_ {i}\ derecha)\\
&=e_ {l}\ izquierda (x_ {i}\ derecha)\ suma_ {k} f_ {k} (i-1) a_ {k l}
\ final {alineado}\]
El algoritmo completo [2] se resume a continuación:
• Inicialización\((i=0): f_{0}(0)=1, f_{k}(0)=0 \text { for } k>0\)
• Iteración\((i=1 \ldots N): f_{k}(i)=e_{k}\left(x_{i}\right) \sum_{j} f_{j}(i-1) a_{j k}\)
• Terminación:\(P\left(x, \pi^{*}\right)=\sum_{k} f_{k}(N)\)
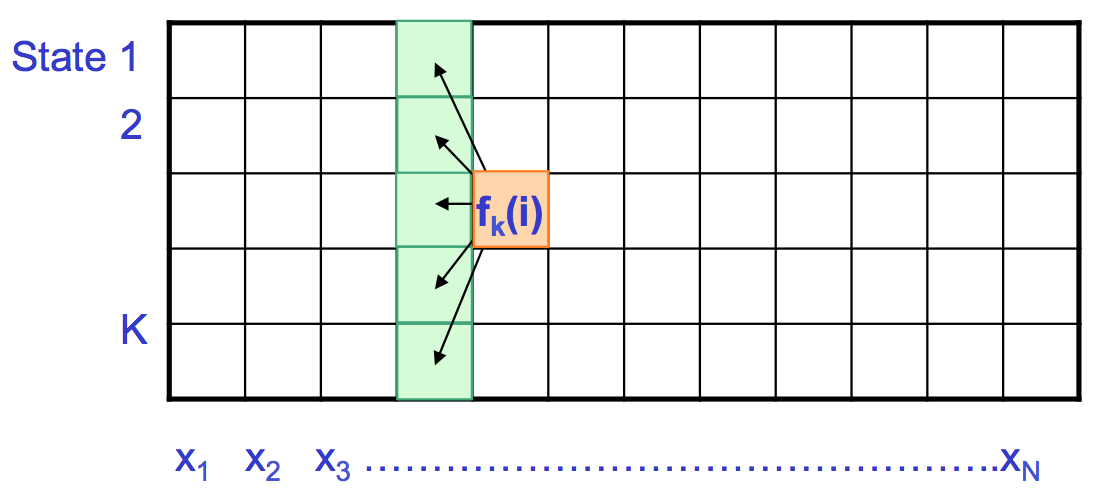
De la Figura 7.17, se puede observar que el algoritmo Forward es muy similar al algoritmo de Viterbi. En el algoritmo Forward, se utiliza la suma en lugar de la maximización. Aquí podemos reutilizar cálculos del problema anterior incluyendo penalización de emisiones, penalización de transiciones y sumas de estados anteriores. El tiempo de cálculo requerido es O (K 2 N) y el espacio requerido es O (KN). El inconveniente de este algoritmo es que en la práctica, tomar la suma de logs es difícil; por lo tanto, en su lugar se utilizan aproximaciones y escalado de probabilidades.


