17.1: Representación de Motivos y Contenido de Información
- Page ID
- 54210
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En lugar de una Matriz de Perfil, también podemos representar Motivos usando la teoría de la información. En la teoría de la información, la información sobre un determinado evento se comunica a través de un mensaje. La cantidad de información transportada por un mensaje se mide en bits. Podemos determinar los bits de información transportados por un mensaje observando la distribución de probabilidad del evento descrito en el mensaje. Básicamente, si no sabemos nada sobre el resultado del evento, el mensaje contendrá muchos bits. No obstante, si estamos bastante seguros de cómo va a llevarse a cabo el evento, y el mensaje sólo confirma nuestras sospechas, el mensaje lleva muy pocos bits de información. Por ejemplo, La sentencia 0un se levantará mañana” no es muy sorprendente, por lo que la información de esa sentencia si es bastante baja.. No obstante, la sentencia 0un no se levantará mañana” es muy sorprendente y tiene un alto contenido de información. Podemos calcular la cantidad específica de información en un mensaje dado con la ecuación: − log p.
La entropía de Shannon es una medida de la cantidad esperada de información contenida en un mensaje. En otras palabras, es la información contenida por un mensaje de cada evento que posiblemente pueda ocurrir ponderada por cada probabilidad de eventos. La entropía de Shannon viene dada por la ecuación:
\[ H(X)=-\sum_{i} p_{i} \log _{2} p_{i} \nonumber \]
La entropía es máxima cuando todos los eventos tienen la misma probabilidad de ocurrir. Esto se debe a que la Entropía nos dice la cantidad esperada de información que aprenderemos. Si cada uno incluso tiene las mismas posibilidades de ocurrir sabemos lo menos posible sobre el evento, por lo que se maximiza la cantidad esperada de información que aprenderemos. Por ejemplo, un volteo de moneda tiene una entropía máxima solo cuando la moneda es justa. Si la moneda no es justa, entonces sabemos más sobre el evento de la volteo de moneda, y el mensaje esperado del resultado del flip de moneda contendrá menos información.
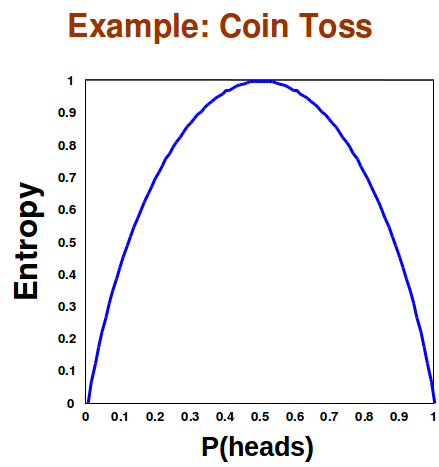
Figura 17.11: La entropía se maximiza cuando tanto la cabeza como la cola tienen la misma probabilidad de ocurrir
Podemos modelar un motivo por la cantidad de información que tenemos de cada posición después de aplicar Gibs Sampling o EM. En la siguiente figura, la altura de cada letra representa el número de bits de información que hemos aprendido sobre esa base. Las pilas más altas corresponden a una mayor certeza sobre cuál es la base en esa posición del motivo, mientras que las pilas inferiores corresponden a un mayor grado de incertidumbre. Con cuatro codones para elegir, la Entropía Shannon de cada posición es de 2 bits. Otra forma de observar esta figura es que la altura de una letra es proporcional a la frecuencia de la base en esa posición.
Figura 17.12: La altura de cada pila representa el número de bits de información que el muestreo de Gibbs o EM nos contó sobre la posición en el motivo
Hay una métrica de distancia en las distribuciones de probabilidad conocida como distancia Kullback-Leibler. Esto nos permite comparar la divergencia de la distribución de motivos con alguna distribución verdadera. La distancia K-L viene dada por
\[ D_{K L}\left(P_{\text {motif}} \mid P_{\text {background}}\right)=\Sigma_{A, T, G, C} P_{\text {motif}}(i) \log \underset{P \text {background}(i)}{P_{\text {motif}}(i)} \nonumber \]
En Plasmodium, hay un menor contenido de G-C. Si asumimos un contenido de G-C del 20%, entonces obtenemos la siguiente representación para el motivo anterior. Las bases C y G son mucho más inusuales, por lo que su prevalencia es muy inusual. Tenga en cuenta que en esta representación, se utilizó la distancia K-L, de manera que es posible que la pila sea superior a 2.
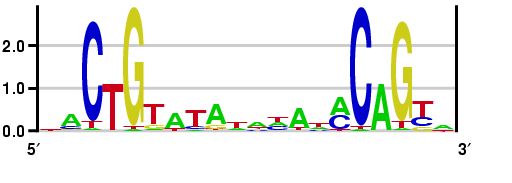
Figura 17.13: Sitio de unión LexA asumiendo bajo contenido de G-C y usando distancia K-L
Bibliografía
- [1] Timothy L. Bailey. Ajustar un modelo de mezcla por maximización de expectativas para descubrir motivos en biopolímeros. En Actas de la Segunda Conferencia Internacional sobre Sistemas Inteligentes para la Biología Molecular, páginas 28—36. Prensa AAAI, 1994.
- [2] C E Lawrence y A A Reilly. Un algoritmo de maximización de expectativas (em) para la identificación y caracterización de sitios comunes en secuencias de biopolímeros no alineados. Proteínas, 7 (1) :41—51, 1990.