20.2: Medidas de Centralidad de Red
- Page ID
- 54813
Se discutió en el capítulo anterior cómo podemos tomar una red biológica y modelarla matemáticamente. Ahora como visualizamos estas gráficas y tratamos de entenderlas necesitamos alguna medida por la importancia de un nodo/borde a las características estructurales del sistema. Hay muchas maneras de medir la importancia (lo que denominamos centralidad) de un nodo. En este capítulo exploraremos estas ideas e investigaremos su significación.
Centralidad de Titulación
La primera idea sobre la centralidad es medir la importancia por el grado de un nodo. Esta es probablemente una de las medidas de centralidad más intuitivas ya que es muy fácil de visualizar y razonar. Cuantos más bordes tengas conectados contigo, más importante para la red eres.
Exploremos un ejemplo sencillo y veamos cómo se trata de encontrar estas centralidades. Tenemos la siguiente gráfica
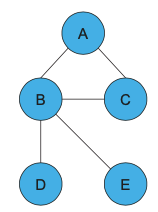
Y nuestro objetivo es encontrar la centralidad de grado de cada nodo en la gráfica. Para proceder, primero escribimos la matriz de adyacencia para esta gráfica. El orden de los bordes es A, B, C, D, E
\ [A=\ left [\ begin {array} {lllll}
0 & 1 & 0 & 0 & 0\\
1 & 0 & 1 & 1 &
1\\ 1 & 1 & 0 & 0 &
0 & 0 & 0 & 0 & 0 &
0 & 0 & 0 & 0 & 0
\ end {array} \ derecho]\]
Anteriormente discutimos cómo encontrar el grado para un nodo dado una matriz de adyacencia. Sumamos a lo largo de cada fila de la matriz de adyacencia.
\ [D=\ left [\ begin {array} {l}
1\\
4\\
3\\
1\\
1
\ end {array}\ derecha]\]
Ahora D es un vector con el grado de cada nodo. Este vector nos da unas medidas de centralidad relativa para los nodos de esta red. Podemos observar que el nodo B tiene el grado más alto de centralidad.
Aunque esta métrica nos da mucha perspicacia, tiene sus limitaciones. Imagine una situación en la que haya un nodo que conecte dos partes de la red entre sí. El nodo tendrá un grado de 2, pero es mucho más importante que eso.
Centralidad entre
La centralidad entre medias nos da otra forma de pensar sobre la importancia en una red. Mide el número de caminos más cortos en la gráfica que pasan por el nodo dividido por el número total de caminos más cortos. En otras palabras, esta métrica calcula todas las rutas más cortas entre cada par de nodos y ve cuál es el porcentaje de que pasa por el nodo k, ese porcentaje nos da la centralidad para el nodo k.
• Nodos con centralidad de alto entremezclamiento controlan el flujo de información en una red.
• El entreborde se define de manera similar.
Cercanía Centralidad
Para definir adecuadamente la cercanía necesitamos definir el término distancia. La distancia entre dos nodos es la ruta más corta entre ellos. La distancia de un nodo es la suma de distancias entre ese nodo y todos los demás nodos. Y la cercanía de un nodo es la inversa de su distancia. En otras palabras, es el inverso normalizado de la suma de distancias topológicas en la gráfica.
El nodo más central es el nodo que propaga la información más rápido a través de la red.
La descripción de la centralidad de la cercanía la hace similar a la centralidad del grado. ¿El más alto grado de centralidad es siempre la más alta centralidad de cercanía? No. Piense en el ejemplo donde un nodo conecta dos componentes, ese nodo tiene una centralidad de bajo grado pero una centralidad de alta cercanía.
Centralidad Eigenvector
La centralidad de los vectores propios extiende el concepto de grado. Lo mejor para pensarlo es el promedio de las centralidades de sus vecinos de la red. El vector de centralidades puede escribirse como:
\[x=\frac{1}{\lambda} A x \nonumber \]
donde A es la matriz de adyacencia. La solución a la ecuación anterior va a ser el vector propio correspondiente al componente principal (el valor propio más grande).
La siguiente sección incluye una revisión de conceptos de álgebra lineal incluyendo valores propios y vectores propios.


