20.4: Análisis de componentes principales dispersos

Limitaciones del Análisis de Componentes Principales

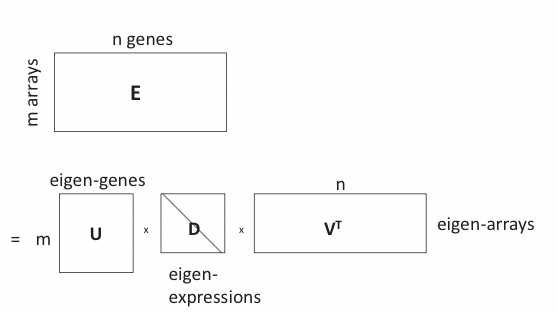
Al analizar datos de expresión génica basados en micromatrices, a menudo estamos tratando con matrices de datos de dimensiones\(m \times n\) donde m es el número de matrices y n es el número de genes. Por lo general n está en el orden de miles y m está en el orden de cientos. Nos gustaría identificar las características más importantes (genes) que mejor explican la variación de expresión, o patrones, en el conjunto de datos. Esto se puede hacer realizando PCA en la matriz de expresión:

\[\mathbf{E}=\mathbf{U D V}^{T} \nonumber \]

Esto es en esencia un SVD de la matriz de expresión E que gira y escala el espacio de características para que los vectores de expresión de cada gen en el nuevo sistema de coordenadas ortogonales estén lo más descorrelacionados posible, donde E es la matriz de expresión m por n, U es la matriz m por m de vectores singulares izquierdos (es decir, principal componentes), o “genes propios”, V es la matriz n por n de vectores singulares derechos, o “matrices propias”, y D es una matriz diagonal de valores singulares, o “expresiones propias” de genes propios. Esto se ilustra en la Figura 20.6.

En PCA, cada componente principal (eigen-gen, una columna de U) es una combinación lineal de n variables (genes), que corresponde a un vector de carga (columna de V) donde las cargas son coecientes correspondientes a variables en la combinación lineal.

Sin embargo, una aplicación directa de PCA a matrices de expresión o cualquier matriz de datos grandes puede ser problemática porque los componentes principales (genes propios) son combinaciones lineales de todas las n variables (genes), lo cual es difícil de interpretar en términos de relevancia funcional. En la práctica nos gustaría utilizar una combinación del menor número posible de genes para explicar los patrones de expresión, lo que se puede lograr mediante una versión dispersa de PCA.

fuente desconocida. Todos los derechos reservados. Este contenido está excluido de nuestra licencia Creative Commons. Para obtener más información, consulte http://ocw.mit.edu/help/faq-fair-use/.

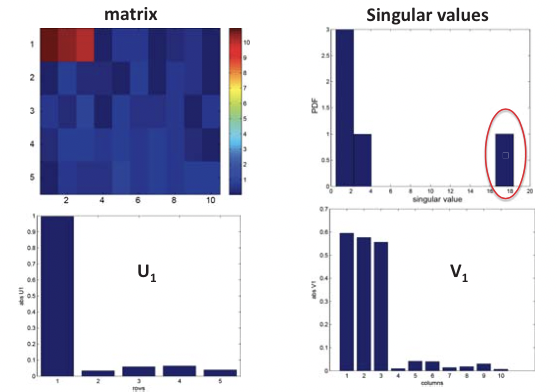
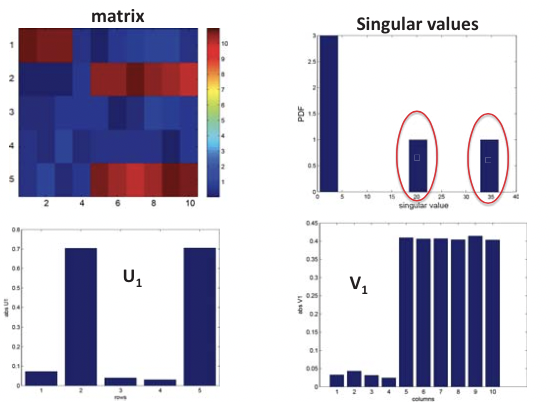
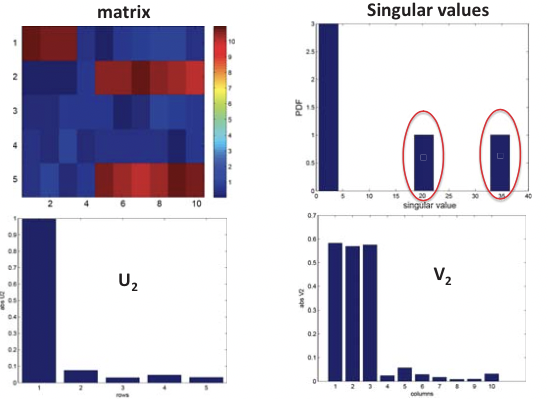
Figura 20.5: Inferencia estructural usando SVD

PCA disperso

El PCA disperso (SPCA) modifica el PCA para limitar los componentes principales (PC) a tener cargas escasas, reduciendo así el número de variables utilizadas explícitamente (genes en datos de microarrays, etc.) y facilitando la interpretación. Esto se hace formulando PCA como un problema de optimización de tipo regresión lineal e imponiendo restricciones de dispersión.

Un problema de regresión lineal toma un conjunto de variables de entrada x = (1, x ₁,... , x _p) y las variables de respuesta\(\mathbf{y}=\mathbf{x} \beta+\epsilon\) donde\(\beta\) es un vector de fila de coeficientes de regresión\(\left(\beta_{0}, \beta_{1}, \ldots, \beta_{p}\right)^{T}\) y\(\epsilon\) es el error. El modelo de regresión para N observaciones se puede escribir en forma de matriz:

\ [\ left [\ begin {array} {c}
y_ {1}\\
y_ {2}\\
\ vdots\\
y_ {N}
\ end {array}\ right] =\ left [\ begin {array} {ccccc}
1 & x_ {1,1} & x_ {1,2} &\ cdots & x_ {1, p}\\
1 & x_ {2,1} & _ {2,2} &\ cdots & x_ {2, p}\\
\ vdots &\ vdots &\ vdots &\ ddots &\ vdots\\ vdots\\
1 & x_ {N, 1} & x_ {N, 2} &\ cdots & x_ {N, p}
\ end {array}\ derecha]\ left [\ begin {array} {c}
\ beta_ {0}
\\ beta_ {}\\
\ vdots\\
\ beta_ {p}
\ end {array}\ derecha] +\ izquierda [\ begin {array} {c}
\ epsilon_ {1}\\
\ epsilon_ {2}\\
\ vdots\\
\ epsilon_ {N}
\ end {array}\ derecha]\]

El objetivo del problema de regresión lineal es estimar los coeficientes\(\beta\). Hay varias formas de hacerlo, y los métodos más utilizados incluyen el método de mínimos cuadrados, el método Lasso y el método de la red elástica.

El método de mínimos cuadrados minimiza la suma residual del error cuadrado:

Figura 20.6: Descomposición del gen propio usando PCA

\[\hat{\beta}=\operatorname{argmin}_{\beta}\{R S S(\beta) \mid D\} \]

donde\(R S S\left(\beta \equiv \sum_{i=1}^{N}\left(y_{i}-X_{i} \beta\right)^{2}\right.\) (X _i es la i-ésima instancia de las variables de entrada x). Esto se ilustra en la Figura 20.7 para los casos 2-D y 3-D, donde se produce una línea de regresión o un hiperplano.

fuente desconocida. Todos los derechos reservados. Este contenido está excluido de nuestra licencia Creative Commons. Para obtener más información, consulte http://ocw.mit.edu/help/faq-fair-use/.

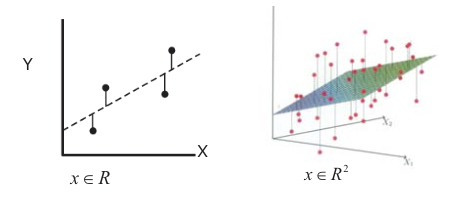
Figura 20.7: Solución de mínimos cuadrados de regresión lineal. Izquierda: 2-D caso, derecha: 3-D caso

El método de lazo no solo minimiza la suma de errores residuales sino que al mismo tiempo minimiza una penalización de Lazo, que es proporcional a la norma L-1 del vector coffieciente\(\beta\):

\[\hat{\beta}=\operatorname{argmin}_{\beta}\left\{R S S(\beta)+L_{1}(\beta) \mid D\right\} \]

donde\(L_{1}(\beta)=\lambda \sum_{j=1}^{p}\left|\beta_{j}\right|, \lambda \geq 0\) La penalización ideal para PCA dispersa es la norma L ₀ que penaliza a j=1 cada elemento distinto de cero por 1, mientras que los elementos cero son penalizados por 0. Sin embargo, la función de penalización L ₀ no es convexa y la mejor solución para explorar el espacio exponencial (número de combinaciones posibles de elementos distintos de cero) es NP-duro. La norma L ₁ proporciona una aproximación convexa a la norma L ₀. El modelo de regresión Lasso en esencia reduce continuamente los coecientes hacia cero tanto como sea posible, produciendo un modelo escaso. Selecciona automáticamente para el conjunto más pequeño de variables que explican variaciones en los datos. Sin embargo, el método Lasso suers del problema de que si existe un grupo de variables altamente correlacionadas tiende a seleccionar solo una de estas variables. Además, Lasso selecciona como máximo N variables, es decir, el número de variables seleccionadas está limitado por el tamaño de la muestra.

El método Elastic Net elimina la limitación de selección de grupo del método Lasso agregando una restricción de arista:

\[\hat{\beta}=\operatorname{argmin}_{\beta}\left\{R S S(\beta)+L_{1}(\beta)+L_{2}(\beta) \mid D\right\}\]

donde\(L_{2}(\beta)=\lambda_{2} \sum_{j=1}^{p}\left|\beta_{j}\right|^{2}, \quad \lambda_{2} \geq 0\). En la solución de red elástica, se seleccionará un grupo de variables altamente correlacionadas una vez que se incluya una de ellas.

Todos los términos de penalización añadidos anteriores surgen del marco teórico de regularización. Nos saltamos las matemáticas detrás de la técnica y señalamos una explicación concisa en línea y un tutorial de regularización en http://scikit-learn.org/stable/modul...ear_model.html.

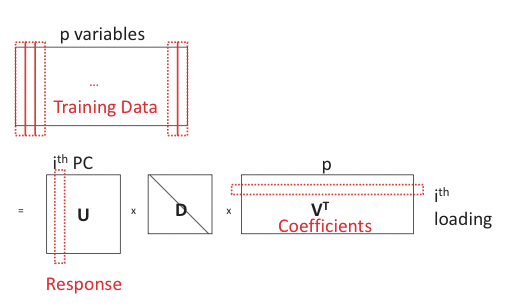
El PCA puede ser reconstruido en un marco de regresión viendo cada PC como una combinación lineal de las variables p. Sus cargas pueden ser recuperadas por PC retrocediendo sobre las variables p (Figura 20.8). Dejar\(\mathbf{x}=\mathbf{U D V}^{T} . \forall i\), denotar Y _i = U _i D _ii, entonces Y _i es el i-ésimo componente principal de X. Nosotros declaramos sin probar el siguiente teorema que confirma la corrección de la reconstrucción:

Teorema 20.4.1. \(\forall \lambda>0\),\(\text {suppose } \hat{\beta}_{\text {ridge}}\) es la estimación de cresta dada por

\[\hat{\beta}_{\text {ridge}}=\operatorname{argmin}_{\beta}\left|Y_{i}-X_{i} \beta\right|^{2}+\lambda|\beta|^{2}\nonumber\]

\[\text {and let } \hat{\mathbf{v}}=\frac{\hat{\beta}_{\text {ridge}}}{\left|\beta_{\text {ridge}}\right|}, \text {then } \hat{\mathbf{v}}=V_{i} \nonumber \]

Figura 20.8: PCA en un marco de regresión

Tenga en cuenta que la penalización de cresta no penaliza a los coecientes sino que asegura la reconstrucción de los PCs. Tal problema de regresión no puede servir como alternativa al PCA ingenuo ya que usa exactamente sus resultados U en el modelo, pero puede modificarse agregando la penalización de Lazo al problema de regresión para penalizar por los valores absolutos de los coeficientes:

\[\hat{\beta}_{\text {ridge}}=\operatorname{argmin}_{\beta}\left|Y_{i}-X_{i} \beta\right|^{2}+\lambda|\beta|^{2}+\lambda_{1}|\beta| \]

donde\(\mathbf{X}=\mathbf{U D V}^{T}\) y\(\forall i, Y_{i}=U_{i} D_{i i}\) es el i-ésimo componente principal de X. Los resultantes\(\hat{\beta}\) cuando se escalan por su norma son exactamente a lo que apunta SPCA: cargas escasas:

\[\hat{V}_{i}=\frac{\hat{\beta}}{|\hat{\beta}|} \approx V_{i}\]
\(X \hat{V}_{i} \approx Y_{i}\)siendo el i-ésimo componente principal disperso.

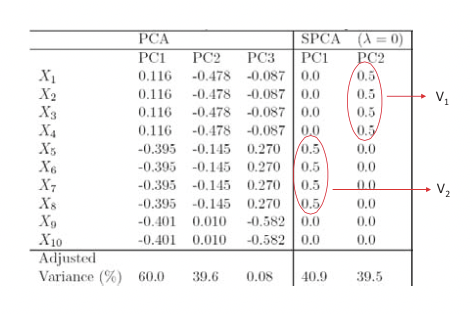
Aquí damos un conjunto de datos de ejemplo simulado y comparamos la recuperación de factores ocultos usando PCA y SPCA. Tenemos 10 variables para las cuales generar puntos de datos: X = (X ₁,..., X ₁₀), y se utiliza un modelo de 3 factores ocultos V ₁, V ₂ y V ₃ para generar los datos:

\ [\ begin {array} {l}
V_ {1}\ sim N (0,290)\\
V_ {2}\ sim N (0,300)\\
V_ {3}\ sim-0.3 V_ {1} +0.925 V_ {2} +e, e\ sim N (0,1)\
X_ {i} =V_ {1} +e_ {i} ^ {1}, e_ {i} ^ {1}\ sim N (0,1), i=1,2,3,4\\
X_ {i} =V_ {2} +e_ {i} ^ {2}, e_ {i} ^ {2}\ sim N (0,1), i=5,6,7,8\\
X_ {i} =V_ {3} +e_ {i} ^ {3}, e_ {i} ^ {3}\ sim N (0,1), i=9,10
\ end {array}\ nonumber\]

De estos datos se espera que dos estructuras significativas surjan de un modelo de PCA disperso, cada una regida por factores ocultos V ₁ y V ₂ respectivamente (V ₃ es meramente una mezcla lineal de los dos). En efecto, como se muestra en la Figura 20.9, al limitar el número de variables utilizadas, SPCA recupera correctamente los PC explicando los efectos de V ₁ y V ₂ mientras que el PCA no distingue bien entre la mezcla de factores ocultos.

Figura 20.9: PCA vs SPCA