20.5: Comunidades y Módulos de Red

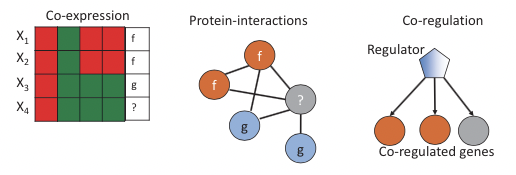
¿Es posible usar redes para inferir las etiquetas de nodos no etiquetados, o datos? Suponiendo que algunos de los datos están etiquetados en una red, podemos usar la idea de que las redes capturan información relacional a través de una metodología de “Culpabilidad por asociación”. En pocas palabras, podemos mirar a los etiquetados “amigos” de un nodo en una red para inferir la etiqueta de un nuevo nodo. A pesar de que la forma de razonamiento “Culpabilidad por asociación” es una falacia lógica e insuficiente en entornos judiciales legales, a menudo es útil predecir etiquetas (por ejemplo, funciones génicas) para nodos en una red mirando las etiquetas de los vecinos de un nodo. Esencialmente, es probable que un nodo conectado a muchos nodos con la misma etiqueta también tenga esa etiqueta. En términos de redes biológicas donde los nodos representan genes, y los bordes representan interacciones (regulación, coexpresión, interacciones proteína-proteína etc., ver Figura 20.11), es posible predecir la función de un gen no anotado en base a las funciones de los genes a los que está conectado el gen consulta. Es fácil ver que podemos aplicar esto inmediatamente en un algoritmo iterativo, donde comenzamos con un conjunto de nodos etiquetados y nodos no etiquetados, y actualizamos iterativamente los atributos relacionales y luego reinferimos etiquetas de nodos. Iteramos hasta que todos los nodos estén etiquetados. Esto se conoce como el algoritmo de clasificación iterativa.

Figura 20.10: El algoritmo de clasificación iterativa

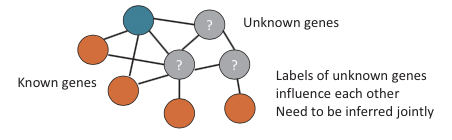
“Culpabilidad por asociación” implica una noción de asociación. La definición de asociación que consideramos implícitamente anteriormente es una definición sencilla donde consideramos todos los nodos conectados directamente a un nodo en particular. ¿Podemos dar una mejor definición de asociación? Considerando esta pregunta, llegamos naturalmente a la idea de comunidades, o módulos, en gráficas. El término comunidad intenta capturar la noción de región en una gráfica con nodos densamente conectados, vinculados a otras regiones de la gráfica con un número escaso de aristas. Las gráficas como estas, con subgrafías densamente conectadas, a menudo se denominan modulares. Obsérvese que no hay consenso sobre la definición exacta de comunidades. Para su uso práctico, la definición de comunidades debe estar motivada biológicamente e informada por conocimientos previos sobre el sistema que se modela. En biología, las redes reguladoras suelen ser modulares, con genes en cada subgrafía densamente conectada que comparten funciones y corregulación similares. Sin embargo, se han desarrollado amplias categorías de comunidades basadas en características topológicas diferentes. Se pueden dividir aproximadamente en 4 categorías: comunidades centradas en nodos, centradas en grupos, centradas en redes y centradas en jerarquías. Aquí examinamos un criterio de uso común para cada uno de los tres primeros tipos y recorremos brevemente algunos algoritmos conocidos que detectan estas comunidades.

Figura 20.11: Predicción de la función génica usando asociaciones

Comunidades centradas en nodos

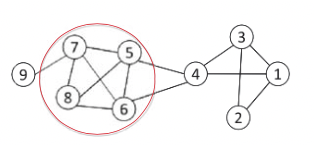
Los criterios de comunidad centrados en nodos generalmente requieren que cada nodo de un grupo satisfaga ciertas propiedades. Una definición de comunidad centrada en nodos de uso frecuente es la camarilla, que es una subgrafía máxima completa en la que todos los nodos son adyacentes entre sí. La Figura 20.12 muestra un ejemplo de una camarilla (nodos 5,6 7 y 8) en una red.

Encontrar exactamente la camarilla máxima en una red es NP-hard, por lo que es muy costoso desde el punto de vista computacional implementar un algoritmo sencillo para la búsqueda de camarillas. La heurística se usa a menudo para limitar la complejidad del tiempo negociando una cierta fracción de precisión. Una heurística de uso común para el hallazgo de camarilla máxima se basa en la observación de que en una camarilla de tamaño k, cada nodo mantiene un grado de al menos k-1. Por lo tanto, podemos aplicar el siguiente procedimiento de poda:

• Muestrear una subred de la red dada y encontrar una camarilla en la subred usando una eficiente

Figura 20.12: Una red de ejemplo que contiene una camarilla de 4

(por ejemplo, codicioso) enfoque

• Supongamos que la camarilla identificada tiene tamaño k, para encontrar una camarilla más grande, se eliminan todos los nodos con grado menor o igual a k-1
• Repita hasta que la red sea lo suficientemente pequeña
  En la práctica se podarán muchos nodos como redes sociales y muchas formas de redes biológicas siguen una ley de poder distribución de grados de nodo que da como resultado un gran número de nodos con grados bajos.

  Tome la red en la Figura 20.12 para un ejemplo de tal procedimiento de búsqueda de camarilla. Supongamos que muestreamos una subred con nodos numerados del 1 al 9 y encontramos una camarilla {1,2,3} de tamaño 3. Para encontrar una camarilla con tamaño mayor a 3, eliminamos iterativamente los nodos al con grado\(\leq\) 2, es decir, los nodos {2, 9}, {1, 3} y 4 se eliminarán secuencialmente. Esto nos deja con la camarilla de 4 {5, 6, 7, 8}.

Comunidades centradas en grupos

Los criterios de comunidad centrados en el grupo consideran las conexiones dentro de un grupo como un todo, y el grupo tiene que satisfacer ciertas propiedades sin hacer zoom en el nivel de nodo, por ejemplo, la densidad de borde del grupo debe exceder un umbral dado. Llamamos a un subgrafo\ G_ {s}\ left (V_ {s}, E_ {s}\ right)\ text {a}\ gamma-\ text {denso}\) una cuasi-camarilla densa si

\[\frac{2\left|E_{s}\right|}{\left|V_{s}\right|\left|V_{s}-1\right|} \geq \gamma \]

donde el denominador es el número máximo de aristas en la red. Con tal definición, se puede adoptar una estrategia similar a la heurística que discutimos para encontrar camarillas máximas:

• Muestree una subred y encuentre una camarilla\(\gamma \) cuasi-densa máxima (por ejemplo, de tamaño |Vs|

• Eliminar nodos con grado menor que el grado promedio\(\left(<\left|V_{s}\right| \gamma \leq \frac{2\left|E_{s}\right|}{\left|V_{s}\right|-1}\right)\)

• Repita hasta que la red sea lo suficientemente pequeña

Comunidades centradas en la red

Las definiciones centradas en la red buscan dividir toda la red en varios conjuntos disjuntos. Existen varios enfoques para tal objetivo, como se enumeran a continuación:

• Algoritmo de agrupamiento de Markov [6]: El Algoritmo de Clustering de Markov (MCL) funciona haciendo una caminata de corrimiento en la gráfica y observando la distribución en estado estacionario de esta caminata. Esta distribución en estado estacionario permite agrupar la gráfica en subgrafías densamente conectadas.
• Algoritmo Girvan-Newman [2]: El algoritmo Girvan-Newman utiliza el número de rutas más cortas que pasan por un nodo para calcular la esencialidad de un borde que luego se puede usar para agrupar la red.
• Algoritmo de partición espectral

En esta sección veremos en detalle el algoritmo de particionamiento espectral. Referimos al lector a las referencias [2, 6] para una descripción de los otros algoritmos.
El algoritmo de partición espectral se basa en una cierta forma de representar una red usando una matriz. Antes de presentar el algoritmo introducimos una descripción importante de una red: su matriz laplaciana.

Matriz laplaciana Para el algoritmo de clustering que presentaremos más adelante en esta sección, necesitaremos contar el número de bordes entre los dos grupos diferentes en una partición de la red. Por ejemplo, en la Figura 21.6a, el número de aristas entre los dos grupos es de 1. La matriz laplaciana que vamos a introducir ahora es útil para representar esta cantidad algebraicamente. La matriz laplaciana L de una red en n nodos es una\(n \times n\) matriz L que es muy similar a la matriz de adyacencia A excepto por los cambios de signo y para los elementos diagonales. Mientras que los elementos diagonales de la matriz de adyacencia son siempre iguales a cero (ya que no tenemos auto-bucles), los elementos diagonales de la matriz Laplaciana mantienen el grado de cada nodo (donde el grado de un nodo se define como el número de aristas que inciden en él). También los elementos fuera de la diagonal de la matriz laplaciana se establecen en -1 en presencia de un borde, y cero en caso contrario. En otras palabras, tenemos:

\[L_{i, j}=\left\{\begin{array}{ll}\operatorname{degree}(i) & \text { if } i=j \\ -1 & \text { if } i \neq j \text { and there is an edge between } i \text { and } j \\ 0 & \text { if } i \neq j \text { and there is no edge between } i \text { and } j\end{array}\right. \]

Por ejemplo, la matriz laplaciana de la gráfica de la figura 21.6b viene dada por (enfatizamos los elementos diagonales en negrita):

\ [L=\ left [\ begin {array} {ccc}
1 & 0 & -1\\
0 & 1 & -1\\
-1 & -1 & 2
\ end {array}\ derecha]\ nonumber\]

Algunas propiedades de la matriz laplaciana La matriz laplaciana de cualquier red disfruta de algunas propiedades agradables que serán importantes más adelante cuando veamos el algoritmo de clustering. Revisamos brevemente estos aquí.

La matriz laplaciana L es siempre simétrica, es decir, L _{i, j} = L _{j, i} para cualquier i, j. Una consecuencia importante de esta observación es que todos los valores propios de L son reales (es decir, no tienen parte imaginaria compleja). De hecho incluso se puede demostrar que los valores propios de L son todos no negativos ² La propiedad final que mencionamos sobre L es que todas las filas y columnas de L suman a cero (esto es fácil de verificar usando la definición de L). Esto significa que el valor propio más pequeño de L es siempre igual a cero, y el vector propio correspondiente es s = (1,1,... ,1).

Contando el número de aristas entre grupos usando la matriz Laplaciana Usando la matriz Laplaciana ahora podemos contar fácilmente el número de aristas que separan dos partes disjuntas de la gráfica usando operaciones simples de matriz. En efecto, supongamos que particionamos nuestra gráfica en dos grupos, y que definimos un vector s de tamaño n que nos dice a qué grupo pertenece cada nodo i:

\ [s_ {i} =\ left\ {\ begin {array} {ll}
1 &\ text {if node} i\ text {está en el grupo} 1\\
-1 &\ text {if node} i\ text {está en el grupo} 2
\ end {array}\ right. \ nonumber\]

Entonces se puede demostrar fácilmente que el número total de aristas entre el grupo 1 y el grupo 2 viene dado por la cantidad\(\frac{1}{4} s^{T} L s\) donde L es el Laplaciano de la red.

Para ver por qué este es el caso, primero calculemos el producto matriz-vector Ls. En particular, fijemos un nodo que digo en el grupo 1 (es decir, s _i = +1) y veamos el componente i'ésimo del producto matriz-vector Ls. Por definición del producto matriz-vector tenemos:

\ (L s) _ {i} =\ suma_ {j = 1} ^ {n} L_ {i, j} s_ {j}\ nonúmero\]

Podemos descomponer esta suma en tres summands de la siguiente manera:

\[(L s)_{i}=\sum_{j=1}^{n} L_{i, j} s_{j}=L_{i, i} s_{i}+\sum_{j \text { in group } 1} L_{i, j} s_{j}+\sum_{j \text { in group } 2} L_{i, j} s_{j} \nonumber \]

Usando la definición de la matriz Laplaciana vemos fácilmente que el primer término corresponde al grado de i, es decir, el número de aristas incidentes a i; el segundo término es igual al negativo del número de aristas que conectan i a algún otro nodo del grupo 1, y el tercer término es igual al número de aristas conectando i a algún nodo ingroup 2. De ahí que tengamos:

(Ls) i = grado (i) (# bordes de i al grupo 1) + (# bordes de i al grupo 2)

Ahora como cualquier borde de i debe ir al grupo 1 o al grupo 2 tenemos

grado (i) = (# bordes de i al grupo 1) + (# bordes de i al grupo 2).

Así combinando las dos ecuaciones anteriores obtenemos:

\[(L s)_{i}=2 \times(\# \text { edges from } i \text { to group } 2) \nonumber \]
Ahora para obtener el número total de aristas entre el grupo 1 y el grupo 2, simplemente sumamos la cantidad sobre todos los nodos i del grupo 1:
\[\text { (# edges between group 1 and group 2) }=\frac{1}{2} \sum_{i \text { in group } 1}(L s)_{i} \nonumber \]

También podemos mirar nodos en el grupo 2 para calcular la misma cantidad y tenemos:

\[\text { (# edges between group 1 and group 2) }=-\frac{1}{2} \sum_{i \text { in group } 2}(L s)_{i}\nonumber \]

Ahora promediando las dos ecuaciones anteriores obtenemos el resultado deseado:

\[\text { (# edges between group 1 and group 2) }=\frac{1}{4} \sum_{i \text { in group } 1}(L s)_{i}-\frac{1}{4} \sum_{i \text { in group 2 }}(L s)_{i}\nonumber\]

\ [\ begin {alineado}
&=\ frac {1} {4}\ suma_ {i} s_ {i} (L s) _ {i}\\
&=\ frac {1} {4} s^ {T} L s
\ final {alineado}\ nonumber\]

donde s ^T es el vector de fila obtenido al transponer el vector de columna s.

El algoritmo de agrupamiento espectral Ahora veremos cómo se puede utilizar la vista de álgebra lineal de las redes dada en la sección anterior para producir una partición “buena” de la gráfica. En cualquier buena partición de una gráfica, el número de aristas entre los dos grupos debe ser relativamente pequeño en comparación con el número de aristas dentro de cada grupo. Así, una forma de abordar el problema es buscar una partición para que el número de aristas entre los dos grupos sea mínimo. Utilizando las herramientas introducidas en la sección anterior, este problema es así equivalente a encontrar un vector\(s \in\{-1,+1\}^{n}\) tomando solo valores -1 o +1 tal que\(\frac{1}{4} s^{T} L s\) sea mínimo, donde L es la matriz Laplaciana de la gráfica. En otras palabras, queremos resolver el problema de minimización:

\[\operatorname{minimize}_{s \in\{-1,+1\}^{n}} \frac{1}{4} s^{T} L s \nonumber \]

Si s ^* es la solución óptima, entonces la partición óptima es asignar el nodo i al grupo 1 si s _i = +1 o bien al grupo 2.

Esta formulación parece tener sentido pero desafortunadamente hay una pequeña falla: la solución a este problema siempre terminará siendo s = (+1,..., +1) lo que corresponde a poner todos los nodos de la red en el grupo 1, ¡y ningún nodo en el grupo 2! El número de aristas entre el grupo 1 y el grupo 2 es entonces simplemente cero y, de hecho, ¡es mínimo!

Para obtener una partición significativa tenemos que considerar así particiones de la gráfica que no son triviales. Recordemos que la matriz laplaciana L es siempre simétrica, y así admite una descomposición propia:

\[L=U \Sigma U^{T}=\sum_{i=1}^{n} \lambda_{i} u_{i} u_{i}^{T} \nonumber\]

donde\( \sigma\) es una matriz diagonal que contiene los valores propios no negativos\(\lambda_{1}, \ldots, \lambda_{n}\) de L y U es la matriz de vectores propios y satisface U ^{T =U-1}.

El costo de una partición\(s \in\{-1,+1\}^{n}\) viene dado por

\[\frac{1}{4} s^{T} L s=\frac{1}{4} s^{T} U \Sigma U^{T} s=\frac{1}{4} \sum_{i=1}^{n} \lambda_{i} \alpha_{i}^{2} \nonumber \]

donde\( \alpha\) = U ^T s dan la descomposición de s como una combinación lineal de los vectores propios de L:\(s=\sum_{i=1}^{n} \alpha_{i} u_{i} \).

Recordemos también eso\(0=\lambda_{1} \leq \lambda_{2} \leq \cdots \leq \lambda_{n}\). Así, una forma de hacer que la cantidad anterior sea lo más pequeña posible (sin escoger la partición trivial) es concentrar todo el peso en 2 que es el valor propio distinto de cero más pequeño de L. Para lograr esto simplemente elegimos s de manera que\( \alpha \) ₂ = 1 y\( \alpha \) _k = 0 para todos \(k \neq 2\). En otras palabras, esto corresponde a tomar s para que sea igual a u ₂ el segundo vector propio de L. Dado que en general el autovector u ₂ no es de valor entero (es decir, los componentes de u2 pueden ser diferentes a -1 o +1), tenemos que convertir primero

Figura 20.13: Una red con 8 nodos.

el vector u ₂ en un vector de +1 o 1. Una manera simple de hacer esto es solo mirar los signos de los componentes de u ₂ en lugar de los valores mismos. Nuestra partición está así dada por:

\ [s=\ nombreoperador {signo}\ izquierda (u_ {2}\ derecha) =\ izquierda\ {\ begin {array} {ll}
1 &\ text {if}\ left (u_ {2}\ derecha) _ {i}\ geq 0\\
-1 &\ text {if}\ left (u_ {2}\ derecha) _ {i} <0
\ end {array} derecha\. \ nonumber\]

Para recapitular, el algoritmo de agrupamiento espectral funciona de la siguiente manera:

Algoritmo de partición espectral Entrada: una red Salida: una partición de la red donde cada nodo se asigna ya sea al grupo 1 o al grupo 2 para que el número de bordes entre los dos grupos sea pequeño Calcular la matriz Laplaciana L de la gráfica dada por: \ [L_ {i, j} =\ left\ {\ begin {array} {ll} \ operatorname {degree} (i) &\ text {if} i=j\\ -1 &\ text {if} i\ neq j\ text {y hay un borde entre} i\ text {y} j\\ 0 &\ text {if} i\ neq j\ text {y no hay borde entre} i\ text {y} j \ end {array}\ right. \ nonumber\] 2. Calcular el autovector u 2 para el segundo valor propio más pequeño de L. 3. Salida de la siguiente partición: Asignar el nodo i al grupo 1 si (u 2) i\(\geq\) 0, de lo contrario asignar el nodo i al grupo 2.

A continuación damos un ejemplo donde aplicamos el algoritmo de clustering espectral a una red con 8 nodos.

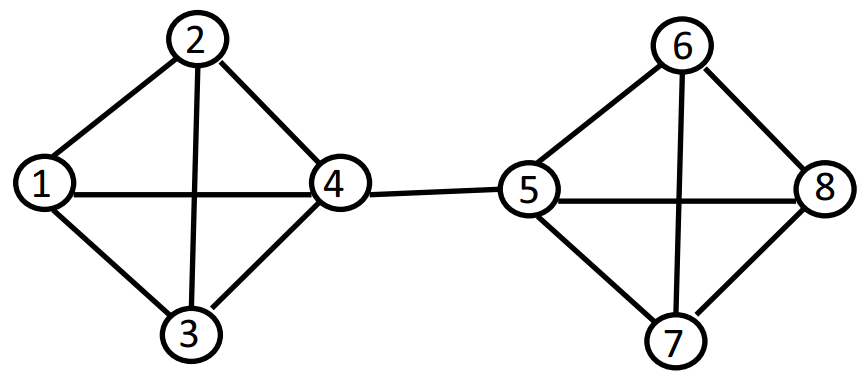
Ejemplo Ilustramos aquí el algoritmo de particionamiento descrito anteriormente en una red simple de 8 nodos dado en la figura 21.7. La matriz de adyacencia y la matriz Laplaciana de esta gráfica se dan a continuación:

\ [A=\ left [\ begin {array} {llllllll}
0 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 &
1 & 0 & 0 & 0 & 0 & 0 & 0 &
1 & 1 & 0 & 1 & 0 & 1 &
amp; 0 & 0 & 0\\
0 & 0 & 1 & 0 & 1 & 1 & 1 & 1\\
0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 1 &
0 & 1 & 1 & 0 & 1 & 0 & 1 &
0 & 1\\ 0 & 0 & 0 & 1 & amp; 1 & 0
\ end {array}\ derecha]\ quad L=\ izquierda [\ begin {array} {rrrrrr}
3 & -1 & -1 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 &
1 & 3 & 0 & 0 & -1 & 0 & 0 & 0
& 0\\
-1 y -1 & 4 & -1 & 0 & 0 & 0 & 0 &
0 & 0 & 0 & 0 & 0 & -1 & 1 & -1 & -1 & -1 & 0 & 0 & 0 & -1 & -1 & -1 & -1\\
0 & 0 & 0 & 0 & -1 &
amp; 3 & -1\\
0 & 0 & 0 & 0 & -1 & -1 & -1 & 3
\ end {array}\ derecha]\ nonumber\]

Usando el comando eig de Matlab podemos calcular la descomposición propia\(L=U \Sigma U^{T}\) de la matriz Laplaciana y obtenemos:

\ [\ begin {aligned}
&U=\ left [\ begin {array} {rrrrrrr}
0.3536 & -0.3825 & 0.2714 & -0.1628 & -0.7783 & 0.0495 & -0.0064 & -0.1426\\
0.3536 & -0.3825 & 0.5580 & -0.1628 & 0.6066 & 0.0495 & -0.0064 & -0.1426\\
0.3536 & -0.3825 & -0.4495 & 0.6251 & 0.0930 & 0.0495 & -0.3231 & -0.1426\\
0.3536 & -0.2470 & -0.3799 & -0.2995 & 0.0786 & -0.1485 & 0.3358 & 0.6626\\
0.3536 &\ mathbf {0. 2 4 7 0} & -0.3799 & -0. 2995 & 0.0786 & -0.1485 & 0.3358 & -0.6626\\
0.3536 &\ mathbf {0. 3 8 2 5} & 0.3514 & 0.5572 & -0.0727 & -0.3466 & 0.3860 & 0.1426\\
0.3536 &\ mathbf {0. 3 8 2 5} & 0.0284 & -0.2577 & -0.0059 & -0.3466 & -0.7266 18 y amp; 0.1426\\
0.3536 &\ mathbf {0. 3 8 2 5} & 0.0000 & 0.0000 & 0.0000 & 0.8416 & -0.0000 & 0.1426
\ end {array}\ right]\\
&\ Sigma=\ left [\ begin {array} {llllllll}
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\
0 & 0.3542 & 0 & 0 & 0 & 0 &
0 & 0 & 0 & 0 & 0 & 0 & 0 &
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 &
0 & 0 & 0 & 0 & 0 & ; 0 & 0\\ 0 &
0 & 0 & 0 & 0 & 0 & 4.0000 & 0 & 0 & 0 & 0 & 0 &
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 &
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 5.6458
\ end {array}
\ derecho] alineado}\ nonumber\]

Hemos resaltado en negrita el segundo valor propio más pequeño de L y el autovector asociado. Para agrupar la red observamos el signo de los componentes de este vector propio. Vemos que los primeros 4 componentes son negativos, y los últimos 4 componentes son positivos. Así, agruparemos los nodos 1 a 4 juntos en el mismo grupo, y los nodos 5 a 8 en otro grupo. Esto parece un buen agrupamiento y de hecho esta es la agrupación “natural” que se considera a primera vista de la gráfica.

¿Sabías?

El problema matemático que formulamos como motivación para el algoritmo de agrupamiento espectral es encontrar una partición de la gráfica en dos grupos con un número mínimo de bordes entre los dos grupos. El algoritmo de particionamiento espectral que presentamos no siempre da una solución óptima a este problema pero suele funcionar bien en la práctica.

En realidad resulta que el problema tal y como lo formulamos se puede resolver exactamente usando un algoritmo eciente. El problema a veces se llama el problema de corte mínimo ya que estamos buscando cortar un número mínimo de bordes de la gráfica para desconectarla (los bordes que cortamos son los que se encuentran entre el grupo 1 y el grupo 2). El problema de corte mínimo se puede resolver en tiempo polinomial en general, y remitimos al lector a la entrada de Wikipedia sobre corte mínimo [9] para más información. El problema sin embargo con las particiones de corte mínimo es que generalmente conducen a particiones de la gráfica que no están equilibradas (por ejemplo, un grupo tiene solo 1 nodo, y los nodos restantes están todos en el otro grupo). En general, uno quisiera imponer restricciones adicionales a los clústeres (por ejemplo, límites inferiores o superiores en el tamaño de los clústeres, etc.) para obtener clústeres más realistas. Con tales limitaciones, el problema se vuelve más difícil, y remitimos al lector a la entrada de Wikipedia sobre Particionamiento gráfico [8] para más detalles.

Preguntas frecuentes

P: ¿Cómo dividir la gráfica en más de dos grupos?

R: En esta sección solo nos fijamos en el problema de particionar la gráfica en dos clústeres. ¿Y si queremos agrupar la gráfica en más de dos clústeres? Hay varias extensiones posibles del algoritmo que se presentan aquí para manejar k clústeres en lugar de solo dos. La idea principal es mirar los k vectores propios para los k valores propios distintos de cero más pequeños del Laplaciano, y luego aplicar el algoritmo de clustering k-means apropiadamente. Refirimos al lector al tutorial [7] para más información.

---

² Una forma de ver esto es notar que L es diagonalmente dominante y los elementos diagonales son estrictamente positivos (para más detalles el lector puede buscar “diagonalmente dominante” y “teorema del círculo Gershgorin” en Internet).