20.6: Núcleo de Difusión en Red

Anteriormente, definimos una métrica de distancia entre dos nodos como la ruta más corta ponderada. Esta métrica de distancia simple es suciente para muchos propósitos, pero notablemente no utiliza ninguna información sobre la estructura general de la gráfica. Muchas veces, definir la distancia en función del número de caminos posibles entre dos nodos, ponderados por la verosimilitud o probabilidad de tomar tales caminos, da una mejor representación del sistema real que estamos modelando. Exploramos métricas de distancia alternativas en esta sección.

Figura 20.14: ¿Qué otras métricas de distancia son útiles?

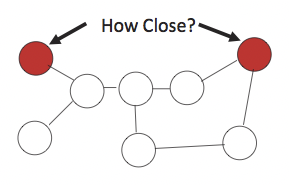
Las matrices de kernel de difusión ayudan a capturar la estructura de red global de los gráficos, informando una definición más compleja de distancia.

Que A sea nuestra matriz de adyacencia regular. D es la matriz diagonal de grados. Podemos definir L, la matriz laplaciana, de la siguiente manera:

\[L=D-A\nonumber\]

Luego definimos un núcleo de difusión K como

\[K=\exp (-\beta L) \nonumber \]
Dónde\(\beta\) está el parámetro de difusión. Tenga en cuenta que estamos tomando una matriz exponencial y no una exponencial por elementos, que se basa en la expansión de la serie Taylor de la siguiente manera:

\[=\sum_{k=0}^{\infty} \frac{1}{k}(-\beta L)^{k} \nonumber \]

Entonces, ¿qué representa la matriz K? Hay múltiples formas de interpretar K, enumeraremos las más relevantes para nosotros a continuación:

Caminatas aleatorias — Una forma de interpretar K como el resultado de una caminata aleatoria. Supongamos que tenemos una gráfica y en el nodo de interés, tenemos una distribución de probabilidad sobre los bordes que representa esa probabilidad de que nos movemos a lo largo de ese borde. Al igual que la siguiente figura:

Figura 20.15: Ilustración de una caminata aleatoria

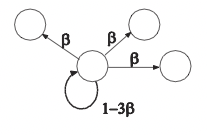
\(\beta\)es la probabilidad de transición a lo largo de un borde específico. Y también hay una probabilidad de que no nos movemos (representado aquí como un bucle self). Tenga en cuenta que para que la distribución de probabilidad sea válida debe sumar hasta 1.

Si tenemos la configuración anterior, entonces K _ij es igual a la probabilidad de que la caminata que comenzó en i esté en j después de pasos de tiempo infinitos. Para derivar ese resultado, podemos escribir nuestra gráfica como modelo de Markov y tomar el límite como\(t \rightarrow \infty\)

Proceso estocástico — Otra forma en que podemos interpretar el núcleo de difusión es a través de un proceso estocástico.

• para cada nodo i, considere una variable aleatoria Zi (t)
• dejar que Zi (t) sea la media cero con alguna varianza definida.
• la covarianza para Zi (t) y Zj (t) es cero (independientes entre sí).
• cada variable envía una fracción a los vecinos

  \ [\ begin {array} {c}
  Z_ {i} (t+1) =Z_ {i} (t) +\ beta\ suma_ {j\ neq i}\ izquierda (Z_ {j} (t) -Z_ {i} (t)\ derecha)\\
  Z (t+1) =( I-\ beta L) Z (t)\
  Z\ (t) =( I-\ beta L) ^ {t} Z (0)
  \ end {array}\ nonumber]

dejar que el operador de evolución temporal T (t) sea

\[T(t)=(I-\beta L)^{t} \nonumber \]

entonces la covarianza es igual a

\[\operatorname{Cov}_{i j}(t)=\sigma^{2} T_{i j}(2 t) \nonumber \]

Entonces a medida que\(\Delta t \rightarrow 0\) tomamos conseguimos

\[ \operatorname{Cov}(t)=\sigma^{2} \exp (-2 \beta t L)\nonumber \]