29.2: Conceptos básicos de selección de población
- Page ID
- 53972
Polimorfismos
Los polimorfismos son diferencias de apariencia entre miembros de una misma especie. Muchos de ellos surgen de mutaciones en el genoma. Estas mutaciones, o polimorfismos genéticos, se pueden caracterizar en diferentes tipos.
Polimorfismos de un solo nucleótido (SNP)
• La mutación de una sola base nucleotídica dentro de una secuencia. En la mayoría de los casos, estos cambios no tienen consecuencias. Sin embargo, hay algunos casos en los que la mutación de un solo nucleótido tiene un efecto mayor.
• Por ejemplo, es causada por una de A a T, que provoca un cambio de ácido glutámico (GAG) a valina (GTG) en la hemoglobina.
Número variable de repeticiones en tándem
- Cuando una secuencia corta se repite varias veces, la ADN Polimerasa a veces puede “deslizarse”, haciendo que haga demasiadas o muy pocas copias de la repetición. Esto se llama un.
- Por ejemplo, la enfermedad de Huntingtons que es causada por demasiadas repeticiones del trinucleótido CAG se repite en el gen HTT. Tener más de 36 repeticiones puede llevar a una pérdida gradual del control muscular y a una degradación neurológica severa. Generalmente, cuantas más repeticiones haya, más fuertes serán los síntomas.
Inserción/eliminación
- A través de copia defectuosa o reparación de ADN, o de uno o múltiples nucleótidos puede ocurrir.
- Si la inserción o deleción está dentro de un exón (la región codificante de proteínas de un gen) y no consiste en un múltiplo de tres nucleótidos, ocurrirá a.
- El primer ejemplo son las deleciones en el gen CFTR, que codifica canales de cloruro en los pulmones y puede causar Fibrosis Quística donde el paciente no puede limpiar las mucosas en los pulmones y causa infección
¿Sabías?
El perfil de ADN se basa en repeticiones en tándem de números variables cortos (STR). El ADN se corta con ciertas enzimas de restricción, dando como resultado fragmentos de longitud variable que pueden ser utilizados para identificar a un individuo. Diferentes países utilizan loci diferentes (pero a menudo superpuestos) para estos perfiles. En Norteamérica se utiliza un sistema basado en 13 loci.
Frecuencias de alelos y genotipos
Para entender la evolución de una especie a través del análisis de alelos o genotipos, debemos tener un modelo de cómo se transmiten los alelos de una generación a otra. Es de inmensa importancia que el lector tenga una firme intuición para el modelo Hardy-Weinberg Principle y Wright fisher antes de continuar. Por lo tanto, proporcionaremos aquí un breve recordatorio de modelar la historia de las mutaciones a través de estos métodos. Introducido por primera vez hace más de cien años, el Modelo Wright-Fisher es un modelo matemático de deriva genética en una población. Específicamente, describe la probabilidad de obtener k copias de un nuevo alelo p dentro de una población de tamaño N, con una frecuencia no mutante de q, y cuál será su frecuencia esperada en generaciones sucesivas.
Principio Hardy-Weinberg
Se afirma que las frecuencias de alelos y genotipos dentro de una población permanecerán constantes a menos que exista una influencia externa que los empuje lejos de ese equilibrio.
El principio Hardy-Weinberg se basa en los siguientes supuestos:
• La población observada es muy grande
- La población está aislada, es decir, no hay introducción de otra subpoblación en la población general
- Todos los individuos tienen la misma probabilidad de producir descendencia
- Todo el apareamiento en la población es al azar
- No se producen mutaciones aleatorias en la población de una generación a otra
- La frecuencia alélica impulsa la frecuencia futura del genotipo (el alelo prevalente impulsa el genotipo prevalente
En un Equilibrio Hardy-Weinberg, para dos alelos A y a, que ocurren con probabilidad p y q = 1p, respectivamente, las probabilidades de un individuo escogido aleatoriamente que tenga los genotipos homocigotos AA o aa (pp o qq, respectivamente) o heterocigóticos Aa o aA (2pq) pueden describirse mediante la ecuación:
\[p^{2}|2 p q| q^{2}=1\nonumber\]
Esta ecuación da una tabla de probabilidades para cada genotipo, la cual puede compararse con las frecuencias observadas del genotipo mediante pruebas de error estadístico como la prueba de chi-cuadrado para determinar si el modelo Hardy- Weinberg es aplicable. La Figura 29.1 muestra la distribución de frecuencias de genotipos a diferentes frecuencias alélicas.
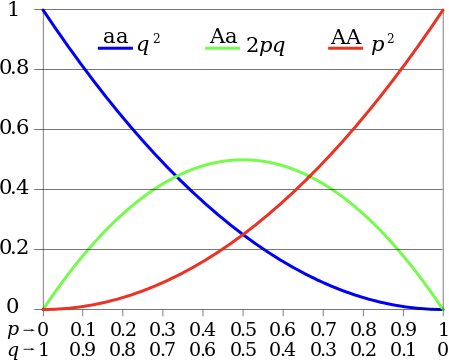
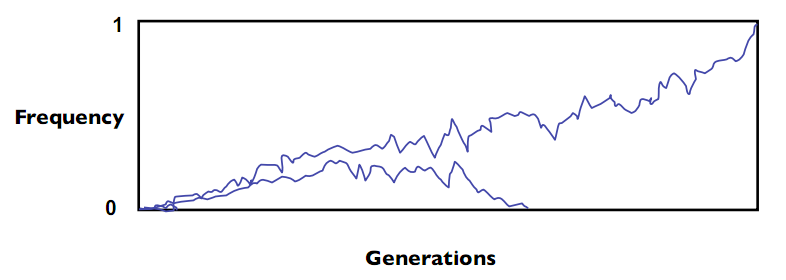
En poblaciones naturales, los supuestos hechos por el principio Hardy-Weinberg rara vez se mantendrán. Se produce la selección natural, las poblaciones pequeñas sufren deriva genética, las poblaciones se dividen o se fusionan, etc. En la naturaleza una mutación siempre desaparecerá (frecuencia = 0) de la población o se volverá prevalente en una especie - esto se llama fijación; en general, el 99% de las mutaciones desaparecen. La Figura 29.2 muestra una simulación de una prevalencia de mutaciones en una población de tamaño finito a lo largo del tiempo: ambas realizan caminatas aleatorias, con una mutación desapareciendo y la otra haciéndose prevalente:
Una vez que una mutación ha desaparecido, la única manera de que reaparezca es la introducción de una nueva mutación en la población. Para los humanos, se cree que una mutación dada bajo ninguna presión selectiva debe fijarse a 0 o 1 (dentro de, por ejemplo, 5%) en unos pocos millones de años. No obstante, bajo selección esto sucederá mucho más rápido.
Modelo Wright-Fisher
Bajo este modelo el tiempo de fijación es 4N y la probabilidad de fijación es 1/2N. En general Wright-Fisher se utiliza para responder preguntas relacionadas con la fijación de una forma u otra. Para asegurarse de que sus intuiciones sobre
Licencia Commons. Para obtener más información, consulte http://ocw.mit.edu/help/faq-fair-use/.
Figura 29.2 Cambios en la frecuencia alélica a lo largo del tiempo.
el método es absolutamente claro considerando las siguientes preguntas:
FAQ
P: Digamos que tiene un total de 5 mutaciones en un cromosoma entre una población de tamaño 30, en promedio, ¿cuántas mutaciones estarán presentes en la próxima generación si cada entidad produce solo un hijo?
R: Si cada progenitor tiene una sola descendencia, entonces habrá, en promedio, 5 mutaciones en la siguiente generación porque la expectativa de frecuencias alélicas es que se mantengan constantes de acuerdo con el principio de equilibrio Hardy-Weinberg en biología básica.
FAQ
P: ¿Es razonable la suposición del principio de Equilibrio Hardy-Weinberg sobre la frecuencia constante de alelos?
R: No, la realidad es mucho más compleja ya que hay estocástico en el tamaño de la población y selección en cada generación. Una forma más apropiada de imaginarlo es dibujar imágenes de alelos de un conjunto de padres, variando la cantidad de alelos en la siguiente generación con el tamaño de la población. De ahí que la frecuencia en la próxima generación muy bien podría subir o bajar. Observe aquí que si la frecuencia alélica va a cero siempre estará en cero. La probabilidad en cada generación sucesiva es menor si está bajo selección negativa y mayor si está bajo selección positiva. De ahí que si se trata de una mutación beneficiosa el tiempo de fijación será menor, si la mutación es perjudicial la fijación será mayor. Si no hay descendencia con una mutación dada, entonces tampoco habrá ningún difunto con esa mutación. Sin embargo, si uno produce múltiples ospring, quienes a su vez producen múltiples crías propias, entonces hay una mayor probabilidad de que esta frecuencia alélica se eleve.
FAQ
P: Considera que el individuo humano promedio lleva aproximadamente 100 mutaciones completamente únicas. Entonces, cuando un individuo produce descendencia podríamos esperar que la mitad (o 50) de esas mutaciones puedan aparecer en el niño porque en cada espermatozoide u óvulo, 50 de esas mutaciones estarán presentes, en promedio. Por lo tanto, es probable que la descendencia de un individuo herede aproximadamente 100 mutaciones, 50 de un progenitor y 50 de otro, además de sus propias mutaciones únicas que provienen de ninguno de los padres. Con esto en mente, uno podría estar interesado en comprender cuáles son las posibilidades de que algunas mutaciones aparezcan en la próxima generación si un individuo produce, digamos, n hijos. ¿Cómo se puede hacer esto?
R: Pista: Para calcular este valor, asumimos que algún alelo se origina en el fundador, en algún cromosoma arbitrario (1 por ejemplo). Entonces nos hacemos la pregunta, ¿cuántos cromosomas 1 existen en toda la población? Por el momento, el tamaño de la población humana es de 7 mil millones, cada uno con dos copias del cromosoma 1.
Las preguntas y respuestas anteriores deberían dejar muy claro que la suposición estándar de Hardy-Weinberg de que las frecuencias alélicas permanecen constantes de una generación a la siguiente se viola en muchos casos naturales, incluyendo migración, mutación genética y selección. En el caso de la selección, este tema se aborda modificando la definición formal para incluir un S, término que mide el sesgo en genotipos debido a la selección. Consulte el cuadro 29.1 para una comparación de las versiones originales y compensadas de selección:
| Comportamiento | Con solo deriva | Con deriva y selección |
| n en la próxima generación | Media: n (=2Np), Dist: Binomial (2N, p) | Media: n (\(n\left(1+\frac{s}{1+n s}\right)\)), Dist: Binomial (2N,\(2 N, p \frac{1+s}{1+p s}\)) |
| Tiempo hasta la fijación | 4N | \(\frac{4 N}{1+\frac{3}{4} N|s|}\left(\frac{1+\frac{1}{2}(\ln N)|s|}{1+|s|}\right)\) |
| Probabilidad de fijación | \(\frac{1}{2 N}\) | \(\frac{1-e^{-2 a}}{1-e^{-4 N s}}\) |
Cuadro 29.1: Comparación del Modelo Wright-Fisher con Deriva, Versus Deriva y Selección
El punto principal a quitar de la Tabla 29.1, y esta sección del capítulo es que el clima tienes selección o no, es muy poco probable que un solo alelo se fije en una población. Si tienes una población muy pequeña, sin embargo, entonces las posibilidades de que se fije un alelo son mucho mejores. Esto suele ser el caso en las poblaciones humanas, donde a menudo hay poblaciones pequeñas, entrecruzadas que permiten que las mutaciones se fijen en una población después de solo unas pocas generaciones, aunque la mutación sea de naturaleza deletérea. Precisamente por eso tendemos a ver trastornos de mandolina deletéreos recesivos en poblaciones aisladas.
Estado Ancestral de Polimorfismos
¿Cómo podemos determinar para un polimorfismo dado qué versión fue la y cuál es la mutante? El estado ancestral se puede inferir comparando el genoma con el de una especie estrechamente relacionada (por ejemplo, humanos y chimpancés) con un árbol filogenético conocido. Las mutaciones pueden ocurrir en cualquier lugar a lo largo del árbol filogenético a veces las mutaciones en la división se fijan de manera diferente en diferentes poblaciones (“diferencia fija”), en cuyo caso las poblaciones enteras difieren en genotipo. Sin embargo, las mutaciones recientes no habrán tenido tiempo suficiente para fijarse, y un polimorfismo estará presente en una especie pero completamente ausente en la otra ya que las mutaciones simultáneas en ambas especies son muy raras. En este caso, la “variante derivada” es la versión del polimorfismo que aparece después de la división, mientras que la variante ancestral es la versión que ocurre en ambas especies.
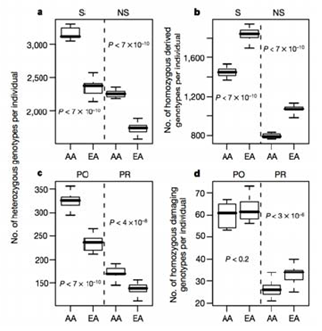
Licencia Commons. Para obtener más información, consulte http://ocw.mit.edu/help/faq-fair-use/.
Figura 30.3: Comparación de los genotipos derivados y dañinos hetrozigóticos y homocigóticos por individuo en un estudio poblacional afroamericano (AA) y europeo americano (EA).
29.2.4 Medición de frecuencias alélicas derivadas
La frecuencia del alelo derivado en la población puede calcularse fácilmente, si asumimos que la población es homogénea. Sin embargo, esta suposición puede no sostenerse cuando existe una división invisible entre dos grupos que hace que evolucionen por separado como se muestra en la figura 29.4.
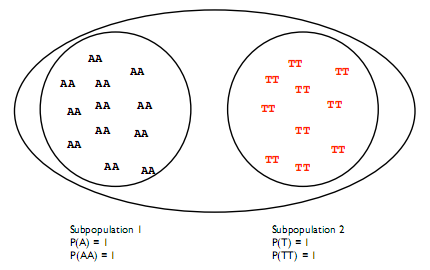
En este caso la prevalencia de las variantes entre subpoblaciones es diferente y se viola el principio de Hardy-Weinberg.
Una forma de cuantificar esta diferencia es usar el (F st) para comparar subpoblaciones dentro de una especie. En realidad, solo una porción de la heterocigosidad total en una especie se encuentra en una subpoblación dada. Fst estima la reducción de heterocigosidad (2pq con alelos p y q) esperada cuando 2 poblaciones diferentes se agrupan erróneamente juntas. Dada una población que tiene n alelos con frecuencias pi donde\((1 \leq i \leq n)\), la homocigosidad G de la población se calcula como:
\[\Sigma_{i=1}^{n} p_{i}^{2}\nonumber\]
La heterocigosidad total en la población viene dada por 1-G.
\[F_{s t}=\frac{H \text {eterozygosity}(\text {total})-\text {Heterozygosity}(\text {subpopulation})}{\text {Heterozygosity}(\text {total})}\nonumber\]
En el caso mostrado en la figura 29.4 no hay heterocigosidad entre las poblaciones, por lo que F st = 1. En realidad el Fst será pequeño dentro de una especie. En humanos, por ejemplo, es sólo 0.0625. Porque en la práctica, el Fst se calcula agrupando subpoblaciones aleatoriamente o usando una característica obvia como etnia u origen.

