3.1: Surge el curioso caso de Bicoid:Modelos para hacer un modelo Gradiente-A

Modelos para Hacer un Degradado

Los gradientes morfogénicos son increíblemente importantes en el desarrollo para modelar los tejidos. Si un tejido es completamente homogéneo (cada célula haciendo la misma tarea) no puede ser complejo y muchas veces no es resistente a las fluctuaciones ambientales. En el caso del Bicoide en Drosophila, estamos considerando un gradiente morfogénico que modela el eje anteroposterior -como se menciona en la Introducción, demasiado Bicoide nos da una cabeza gigante y muy poco nos da ninguna cabeza en absoluto. Hay en algún lugar alrededor de 60 genes diferentes que responden a diversos niveles de proteína Bicoide y uno de los primeros en ser descubierto es Jorobado. Jorobado da información posicional a un embrión de mosca, agudiza el límite entre la parte anterior y posterior de la mosca. Si bien el gradiente de proteínas Bicoides es muy amplio y se asemeja a un gradiente de difusión, el gradiente Jorobado es agudo, con niveles de proteína significativamente diferentes dentro de los 10 μm, o alrededor de 2 núcleos ¹.

Figura 1: El gradiente de Bicoide (Bcd) es poco profundo, la concentración de Bicoide (eje y) se degrada sobre aproximadamente 1/2 de la longitud total del embrión (eje x). Sin embargo, este gradiente superficial proporciona información posicional para el jorobado (Hb), que se traduce siempre y cuando haya niveles incluso bajos de proteína Bicoide1,2. Este agudo gradiente jorobado divide cuidadosamente el embrión en mitades anterior y posterior. Posteriormente en desarrollo, la presencia de Hb alto + Bcd alto, Hb alto, Bcd bajo y bajo Hb + Bcd bajo será leída por diferentes factores de transcripción para producir franjas anchas en el embrión (ver Regionalización y Organizadores para más información).

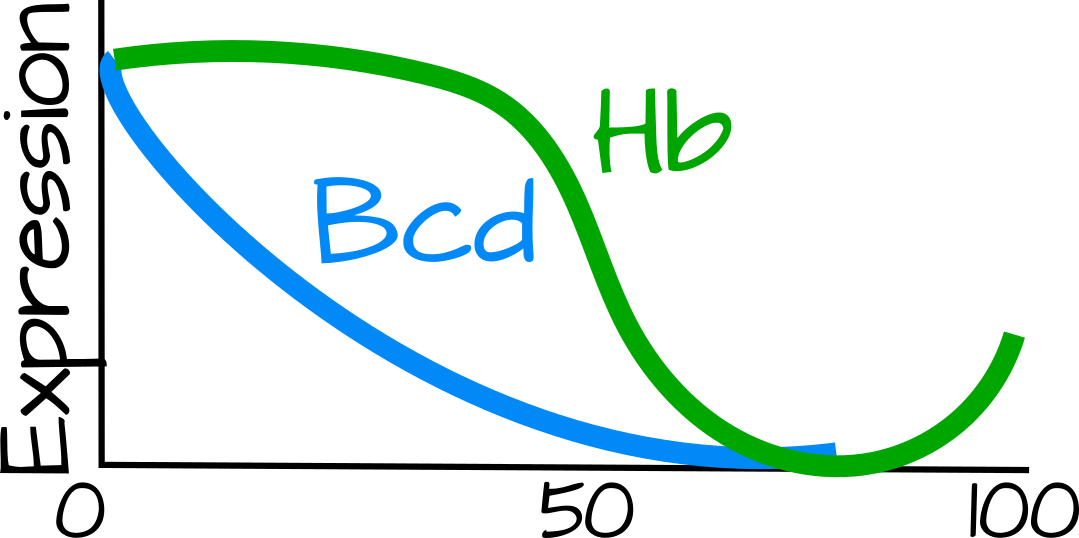
Obviamente los niveles de Bicoid deben importar tremendamente ya que el gradiente Bicoide y su lectura (por ejemplo niveles jorobados) son increíblemente precisos. Un modelo temprano para el gradiente Bicoide observado en Drosophila es el modelo SSD (Síntesis, Soluto, Difusión), donde una fuente puntual de proteína Bicoide (traducida del ARNm bicoide anterior) establece el gradiente de concentración. El modelo SDD relacionado (Síntesis, Difusión, Degradación) incorpora degradación a lo largo del tiempo de la proteína Bicoide, manteniendo el gradiente de alcanzar el extremo posterior del embrión. Se han propuesto varios otros modelos que permitirían la fluctuación en el tamaño del embrión pero que aún así conducirían a una correcta lectura de Bicoides:

1. Más MRN/proteína en embriones más grandes: Esto extendería aún más el gradiente en embriones más grandes.
2. Transbordaje nuclear: Lo mismo que el modelo SDD, pero la proteína Bicoide es captada por los núcleos a medida que se difunde por ellos. Bajo este modelo, cuanto más densamente empaquetados están los núcleos (embrión más pequeño), más rápidamente se saca la proteína Bicoide del citoplasma sincitial. En embriones más grandes, la proteína puede difundirse más lejos.
3. Modelo ARTS (ARNm activo, transporte, síntesis): El citoesqueleto transporta activamente ARNm bicoide para formar un gradiente de ARNm que obtiene lectura como gradiente de proteínas a medida que se traduce. En embriones más grandes, el citoesqueleto puede transportar más el ARNm.
4. Difusión y degradación del ARNm: Esto es similar al modelo ARTS, excepto que en este modelo el ARNm bicoide se degrada con el tiempo para mantener un gradiente de ARNm. Las moscas más grandes podrían tener menores tasas de degradación del ARNm bicoide o un transporte más rápido.
5. Facilitó la difusión de proteínas. Esto es similar al modelo ARTS, sólo que implica el transporte de la proteína Bicoide por el citoesqueleto. En este caso, las moscas más grandes podrían tener un transporte más rápido de la proteína Bicoid.

Hay alguna evidencia a favor y en contra de cada uno de estos modelos, lo que sugiere que el gradiente de proteínas Bicoides probablemente se mantenga mediante una combinación de estos modelos. Además, la lectura de proteínas Bicoid podría ser más compleja de lo que pensamos: múltiples proteínas podrían estar afectando la forma en que Bicoid interactúa con sus dianas.

Pruebas a favor y en contra de los modelos

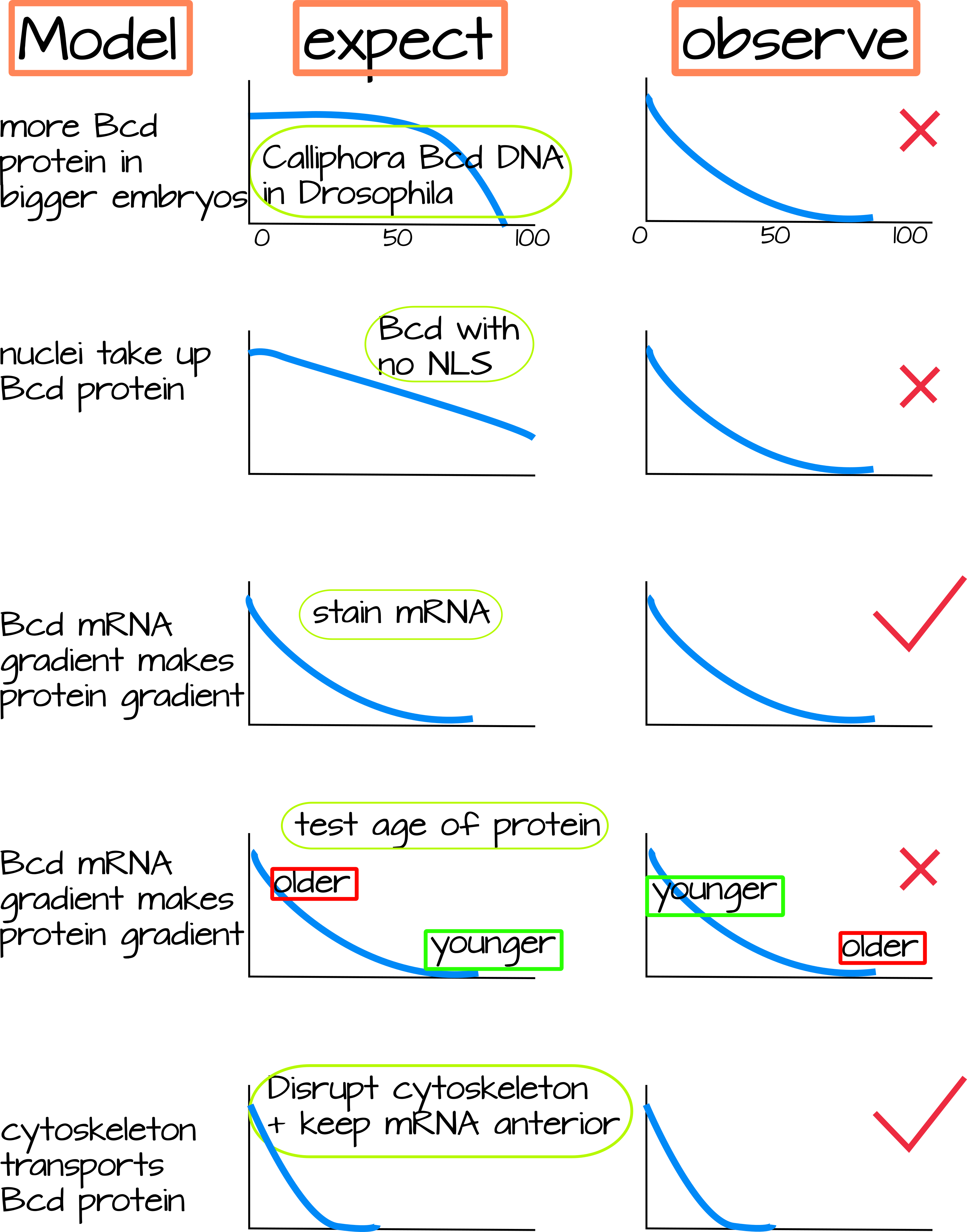
Los datos de Drosophila y otros dípteros más grandes han proporcionado evidencia que respalda cada uno de los modelos enumerados anteriormente. Pruebas adicionales han falsificado las predicciones de algunos de los modelos, y ese es el tema de esta sección. A continuación describo cada modelo y una prueba de ese modelo, también incluyo una figura que ilustra lo que espera el modelo y lo que realmente se observó. Recomiendo este tipo de figura súper reduccionista para ayudar a resumir un gran conjunto de datos, pero siempre hay que tener en cuenta que no cuenta toda la historia.

1. Más modelo de proteína. Un embrión puede obtener más proteína al aumentar la cantidad de ARNm, aumentar la tasa de traducción de ese ARNm o disminuir la tasa de degradación de proteínas. Apoyando esto está el hallazgo de que poner copias adicionales de Bicoid (más ARNm y más proteína) en una mosca de la fruta aumenta el gradiente Bicoide y el tamaño de la cabeza. Para ver si esto es lo que hacen las moscas con embriones más grandes para hacer un gradiente mayor, los investigadores colocaron ADN bicoide, completo con sitios reguladores cis y UTR, de moscas embrionarias grandes (Calliphora) en Drosophila. Encontraron que el gen Bicoide de embriones grandes no hizo un gradiente más largo en Drosophila. Por lo tanto, si hay algún factor que afecte la estabilidad del ARNm o la degradación de proteínas, deben ser específicos de las moscas más grandes ³.

2. Transbordaje nuclear. Los primeros experimentos sobre esto sugirieron que agregar una señal de localización nuclear a la proteína Bicoid hizo un gradiente menos profundo ³. Experimentos posteriores probaron esto haciendo Drosophila con una versión mutante de Bicoid que no se acumuló en los núcleos. Si la importación nuclear hiciera que el gradiente de la proteína Bicoide fuera más pronunciado, entonces habrían visto un gradiente más amplio después de inhibir la importación nuclear. Sin embargo, vieron un gradiente de proteína Bicoide de aspecto bastante normal, argumentando fuertemente en contra de este modelo ⁴.

3 y 4. Modelos de gradiente de ARNm. En ambos modelos 3 y 4, el ARNm es transportado activamente alrededor de la célula por el citoesqueleto. Esto está en oposición directa al modelo SDD, donde la proteína Bicoid se traduce a partir del ARNm bicoide anclado anteriormente. En estos dos modelos de gradiente de ARNm, el gradiente de proteínas es simplemente una “lectura” del gradiente de ARNm. La evidencia de estos dos modelos proviene de la medición cuidadosa del ARNm bicoide en embriones en desarrollo (Figura 2). Estas cuidadosas mediciones muestran que el ARNm bicoide en sí mismo forma un gradiente, y no es simplemente una fuente puntual ⁵. Su movimiento depende del citoesqueleto, si el citoesqueleto se interrumpe, el gradiente de ARNm también se altera ⁶. La evidencia contra este modelo proviene del hallazgo de que la proteína Bicoide en la parte posterior del embrión es más antigua que la proteína Bicoide en la parte anterior. Si el ARNm bicoide se difunde hacia la parte posterior para hacer un gradiente, entonces la proteína Bicoide se elabora a partir de ese ARNm, esperaríamos ver proteína Bicoide más joven en la parte posterior y proteína Bicoide de edad mixta en el extremo anterior. Sin embargo, Durrieu et al encontraron lo contrario, sugiriendo que aunque el ARNm bicoide pueda formar un gradiente, este no es el principal determinante del gradiente proteico ⁷.

5. Facilitó la difusión de proteínas. La interrupción del citoesqueleto mediante el tratamiento de un embrión de Drosophila con fármacos anti-actina o antimicrotúbulos conduce a la alteración del gradiente de proteínas. Dado que la unión de ARNm en el polo anterior también depende de los microtúbulos, solo interrumpir el citoesqueleto no te diría si es el transporte de ARNm o el transporte de proteínas lo que conduce al gradiente de proteínas. Un estudio utilizó un truco divertido: si crías embriones de Drosophila en condiciones de bajo oxígeno (hipóxicas), el ARNm bicoide permanecerá en el extremo anterior incluso si se alteran los microtúbulos. Este estudio encontró que la proteína Bicoide aún forma un gradiente aunque el ARNm de Bicoide no lo haga, y que este gradiente es dependiente del citoesqueleto ⁸.

Figura 2: Evidencia para y contra modelos de gradiente de Bcd ^3,4,5,6,7,8. Se muestran cuatro modelos principales de generación de gradiente Bicoide. Un experimento que soporta o falsifica cada uno se le da un círculo en amarillo. Los gradientes esperados de concentración de Bicoides después de la intervención experimental están a la izquierda, los gradientes de concentración observados están a la derecha.

Surge un modelo

A pesar de todos los datos aparentemente contradictorios, comienza a emerger un modelo que explica la robustez del gradiente de proteína Bicoide y explica cómo el gradiente en sí puede escalar a cuerpos más grandes o más pequeños. Primero, el ARNm bicoide es secuestrado principalmente en el extremo anterior del embrión, pero también viaja a lo largo de la corteza (borde externo) del embrión a través de microtúbulos. La proteína bicoide se traduce fuera del ARNm bicoide, con una mayor cantidad de traducción sucediendo en el extremo anterior, donde la concentración de ARNm bicoide es mayor. Es probable que algunas proteínas bicoides también se traduzcan a partir de la concentración más baja de ARNm bicoide que se ha movido posteriormente a través de microtúbulos. Esto conduce a un gradiente de proteína Bicoide que es ligeramente más amplio de lo que esperaríamos si hubiera una fuente puntual simple de proteína Bicoide (es decir, la traducción del ARNm bicoide del polo anterior).

Este gradiente de proteínas también se modifica a medida que la proteína Bicoide es transportada alrededor del embrión por el citoesqueleto (a través de filamentos de actina y microtúbulos). De esta manera, hay control sobre el gradiente por el citoesqueleto y por las proteínas que median la interacción entre Bicoid (proteína y ARNm) y el citoesqueleto. Estas proteínas mediadoras pueden ser sensibles a los niveles locales de Bicoides y pueden permitir que Bicoid se mueva más rápida o lentamente dependiendo de la posición anteroposterior y el nivel de gradiente. Por ejemplo, una mosca grande podría tener menos proteína Bicoide por difusión al 15% de su longitud (EL) que una mosca pequeña al 15% de su longitud. Sin embargo, toda la proteína Bicoide a 15% EL en la mosca grande puede ser captada por las proteínas mediadoras y movida posteriormente para ampliar el gradiente. Por otro lado, en una mosca pequeña, la mayor cantidad de proteína Bicoid al 15% EL podría sobresaturar la proteína mediadora y transportarse de manera menos eficiente.

Adicionalmente, se sabe que las proteínas bicoides de diferentes especies de mosca tienen propiedades ligeramente diferentes, por ejemplo, el bicoide de especies de moscas más grandes como Calliphora vicinia y Lucilia sericata no son capaces de rescatar completamente Mutantes bicoides de Drosophila ³. Estas diferentes propiedades también podrían desempeñar un papel en las interacciones proteína-proteína que involucran al citoesqueleto. Finalmente, las proteínas mediadoras entre las especies también podrían diferir, algunas podrían unirse a Bicoid de manera más eficiente y/o moverse a lo largo del citoesqueleto de manera más eficiente.