2.2: Prueba Estadística Estándar de Hipótesis
- Page ID
- 53875
Los enfoques estándar de prueba de hipótesis se centran casi por completo en rechazar hipótesis nulas. En el marco (generalmente conocido como el enfoque frecuentista de la estadística) se define primero una hipótesis nula. Esta hipótesis nula representa tu expectativa si algún patrón, como una diferencia entre grupos, no está presente, o si algún proceso de interés no se estaba produciendo. Por ejemplo, quizás te interese comparar el tamaño corporal medio de dos especies de lagartos, un anole y un gecko. Nuestra hipótesis nula sería que las dos especies no difieran en tamaño corporal. La alternativa, que se puede concluir rechazando esa hipótesis nula, es que una especie sea más grande que la otra. Otro ejemplo podría implicar investigar dos variables, como el tamaño corporal y la longitud de las piernas, a través de un conjunto de especies de lagartos 1. Aquí la hipótesis nula sería que no existe relación entre el tamaño corporal y la longitud de la pierna. La hipótesis alternativa, que nuevamente representa la situación en la que realmente se está produciendo el fenómeno de interés, es que existe una relación con el tamaño corporal y la longitud de las piernas. Para los enfoques frecuentistas, la hipótesis alternativa es siempre la negación de la hipótesis nula; como verás a continuación, otros enfoques permiten comparar el ajuste de un conjunto de modelos sin esta restricción y elegir el mejor entre ellos.
El siguiente paso es definir un estadístico de prueba, alguna forma de medir los patrones en los datos. En los dos ejemplos anteriores, consideraríamos estadísticas de prueba que miden la diferencia en el tamaño corporal medio entre nuestras dos especies de lagartos, o la pendiente de la relación entre el tamaño corporal y la longitud de las piernas, respectivamente. Luego se puede comparar el valor de este estadístico de prueba en los datos con la expectativa de este estadístico de prueba bajo la hipótesis nula. La relación entre el estadístico de prueba y su expectativa bajo la hipótesis nula es capturada por un valor P. El valor P es la probabilidad de obtener un estadístico de prueba al menos tan extremo como el estadístico de prueba real en el caso de que la hipótesis nula sea verdadera. Puedes pensar en el valor P como una medida de lo probable que es que obtengas tus datos en un universo donde la hipótesis nula es verdadera. Es decir, el valor P mide lo probable que es bajo la hipótesis nula de que obtengas un estadístico de prueba al menos tan extremo como lo que ves en los datos. En particular, si el valor P es muy grande, digamos P = 0.94, entonces es extremadamente probable que tus datos sean compatibles con esta hipótesis nula.
Si el estadístico de prueba es muy diferente de lo que uno esperaría bajo la hipótesis nula, entonces el valor P será pequeño. Esto significa que es poco probable que obtengamos el estadístico de prueba visto en los datos si la hipótesis nula fuera cierta. En ese caso, rechazamos la hipótesis nula siempre y cuando P sea menor que algún valor elegido de antemano. Este valor es el umbral de significancia, α, y casi siempre se establece en α = 0.05. Por el contrario, si esa probabilidad es grande, entonces no hay nada “especial” en tus datos, al menos desde el punto de vista de tu hipótesis nula. El estadístico de prueba está dentro del rango esperado bajo la hipótesis nula, y fallamos en rechazar esa hipótesis nula. Anote el lenguaje cuidadoso aquí —en un marco frecuentista estándar, nunca aceptas la hipótesis nula, simplemente no la rechazas.
Volviendo a nuestro ejemplo de volteo de lagartos, podemos usar un enfoque frecuentista. En este caso, nuestro ejemplo particular tiene un nombre; se trata de una prueba binomial, que evalúa si un evento dado con dos resultados tiene cierta probabilidad de éxito. En este caso, nos interesa probar la hipótesis nula de que nuestro lagarto es un flipper justo; es decir, que la probabilidad de cabezas p H = 0.5. La prueba binomial utiliza el número de “éxitos” (usaremos el número de cabezas, H = 63) como estadística de prueba. Luego nos preguntamos si este estadístico de prueba es mucho mayor o mucho más pequeño de lo que podríamos esperar bajo nuestra hipótesis nula. Entonces, nuestra hipótesis nula es que p H = 0.5; nuestra alternativa, entonces, es que p H tome algún otro valor: p H ≠ 0.5.
Para llevar a cabo la prueba, primero debemos considerar cuántos “éxitos” debemos esperar si la hipótesis nula fuera cierta. Consideramos la distribución de nuestro estadístico de prueba (el número de cabezas) bajo nuestra hipótesis nula (p H = 0.5). Esta distribución es una distribución binomial (Figura 2.1).
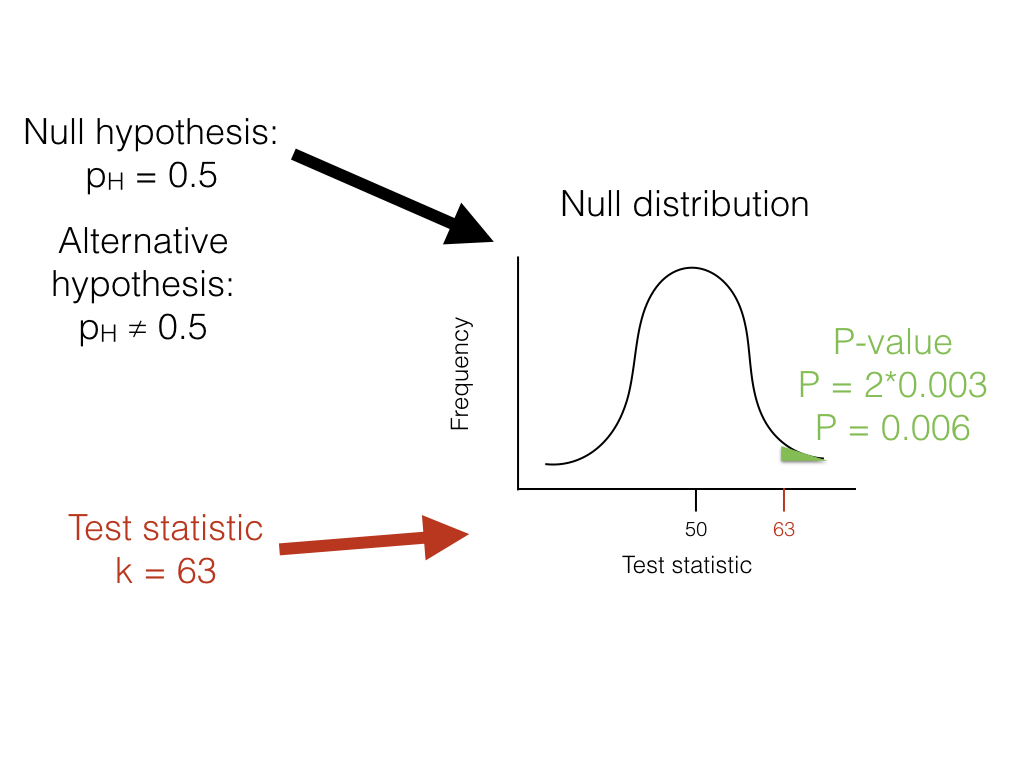
Podemos usar las probabilidades conocidas de la distribución binomial para calcular nuestro valor P. Queremos conocer la probabilidad de obtener un resultado al menos tan extremo como nuestros datos al dibujar a partir de una distribución binomial con parámetros p = 0.5 y n = 100. Calculamos el área de esta distribución que se encuentra a la derecha de 63. Esta área, P = 0.003, se puede obtener ya sea de una tabla, de un software estadístico, o mediante un cálculo relativamente simple. El valor, 0.003, representa la probabilidad de obtener al menos 63 cabezas de 100 ensayos con p H = 0.5. Este número es el valor P de nuestra prueba binomial. Debido a que solo calculamos el área de nuestra distribución nula en una cola (en este caso, la derecha, donde los valores son mayores o iguales a 63), entonces esto es en realidad una prueba de una cola, y solo estamos considerando parte de nuestra hipótesis nula donde p H > 0.5. Tal enfoque podría ser adecuado en algunos casos, pero más típicamente necesitamos multiplicar este número por 2 para obtener una prueba de dos colas; así, P = 0.006. Este valor P de dos colas de 0.006 incluye la posibilidad de resultados tan extremos como nuestro estadístico de prueba en cualquier dirección, ya sea demasiadas o muy pocas cabezas. Desde P < 0.05, nuestro valor α elegido, rechazamos la hipótesis nula, y concluimos que tenemos un lagarto injusto.
En biología, las hipótesis nulas juegan un papel crítico en muchos análisis estadísticos. Entonces, ¿por qué no terminar ahora este capítulo? Una cuestión es que las hipótesis biológicas nulas casi siempre son poco interesantes. A menudo describen la situación en la que los patrones en los datos ocurren solo por casualidad. Sin embargo, si estás comparando especies vivas entre sí, casi siempre hay algunas diferencias entre ellas. De hecho, para la biología, las hipótesis nulas suelen ser obviamente falsas. Por ejemplo, dos especies diferentes que viven en diferentes hábitats no son idénticas, y si las medimos lo suficiente descubriremos este hecho. Desde este punto de vista, ambos resultados de una prueba de hipótesis estándar no son esclarecedores. Uno o rechaza una hipótesis tonta que probablemente se sabía que era falsa desde el principio, o una “falla en rechazar” esta hipótesis nula 2. Hay mucha más información por obtener al estimar los valores de los parámetros y llevar a cabo la selección del modelo en un marco de verosimilitud o bayesiano, como veremos a continuación. Aún así, los enfoques estadísticos frecuentistas son comunes, tienen su lugar en nuestra caja de herramientas, y surgirán en varias secciones de este libro.
Un concepto clave en las pruebas de hipótesis estándar es la idea de error estadístico. Los errores estadísticos vienen en dos sabores: errores tipo I y tipo II. Los errores de tipo I ocurren cuando la hipótesis nula es cierta pero el investigador la rechaza erróneamente. Las pruebas de hipótesis estándar controlan los errores de tipo I usando un parámetro, α, que define la tasa aceptada de errores de tipo I. Por ejemplo, si α = 0.05, uno debería esperar cometer un error de tipo I aproximadamente el 5% del tiempo. Cuando se realizan múltiples pruebas de hipótesis estándar, los investigadores a menudo “corrigen” sus valores P usando la corrección de Bonferroni. Si haces esto, entonces solo hay un 5% de probabilidad de un solo error de tipo I en todas las pruebas que se están considerando. Este singular enfoque en los errores tipo I, sin embargo, tiene un costo. También se pueden cometer errores de tipo II, cuando la hipótesis nula es falsa pero uno no la rechaza. La tasa de errores tipo II en las pruebas estadísticas puede ser extremadamente alta. Mientras que los estadísticos sí se encargan de crear enfoques que tengan un alto poder, las pruebas de hipótesis tradicionales generalmente corrigen errores de tipo I en 5% mientras que las tasas de error de tipo II siguen siendo desconocidas. Existen formas sencillas de calcular las tasas de error de tipo II (por ejemplo, análisis de potencia), pero éstas solo se realizan en raras ocasiones. Además, la corrección de Bonferroni aumenta drásticamente la tasa de error tipo II. Esto es importante porque —como afirma Perneger (1998) — “... los errores de tipo II no son menos falsos que los errores de tipo I”. Este énfasis extremo en controlar los errores de tipo I a expensas de los errores de tipo II es, para mí, la principal debilidad del enfoque frecuentista 3.
Cubriré algunos ejemplos del enfoque frecuentista en este libro, principalmente cuando se discuten métodos tradicionales como los contrastes filogenéticos independientes (PIC). Además, uno de los enfoques de selección de modelos utilizados frecuentemente en este libro, las pruebas de cociente de verosimilitud, se basa en una configuración frecuentista estándar con hipótesis nulas y alternativas.
No obstante, hay dos buenas razones para buscar mejores formas de hacer estadísticas comparativas. En primer lugar, como se indicó anteriormente, los métodos estándar se basan en probar hipótesis nulas que —para cuestiones evolutivas- suelen ser muy probables, a priori, de ser falsas. Para un ejemplo relevante, considere un estudio que compare la tasa de especiación entre dos clados de carnívoros. La hipótesis nula es que los dos clados tienen tasas de especiación exactamente iguales, lo cual es casi seguro falso, aunque podríamos cuestionar cuán diferentes podrían ser las dos tasas. Segundo, en mi opinión, los métodos frecuentistas estándar ponen demasiado énfasis en los valores P y no lo suficiente en el tamaño de los efectos estadísticos. Un valor P pequeño podría reflejar un efecto grande o tamaños de muestra muy grandes o ambos.
En resumen, los métodos estadísticos frecuentistas son comunes en la estadística comparativa pero pueden ser limitantes. Voy a discutir estos métodos a menudo en este libro, principalmente debido a su uso prevalente en el campo. Al mismo tiempo, buscaremos alternativas siempre que sea posible.


