2.4: Estadística Bayesiana

En los últimos años se ha visto un tremendo crecimiento de enfoques bayesianos en la reconstrucción de árboles filogenéticos y la estimación de la longitud de sus ramas. Aunque actualmente solo existen unos pocos métodos comparativos bayesianos, su número sin duda crecerá a medida que los biólogos comparativos intenten resolver problemas más complejos. En un marco bayesiano, la cantidad de interés es la probabilidad posterior, calculada usando el teorema de Bayesiano:

\[ Pr(H|D) = \dfrac{Pr(D|H) \cdot Pr(H)}{Pr(D)} \label{2.19}\]

El beneficio de los enfoques bayesianos es que nos permiten estimar la probabilidad de que la hipótesis sea verdadera dados los datos observados,\(Pr(H|D)\). Este es realmente el tipo de probabilidad que la mayoría de las personas tienen en mente cuando piensan en los objetivos de su estudio. Sin embargo, el teorema de Bayes también revela un costo de este enfoque. Junto con la verosimilitud\(Pr(D|H)\),, también se deben incorporar conocimientos previos sobre la probabilidad de que cualquier hipótesis dada sea verdadera - P r (H). Esto representa la creencia previa de que una hipótesis es cierta, incluso antes de la consideración de los datos en cuestión. Esta probabilidad previa debe cuantificarse explícitamente en todos los análisis estadísticos bayesianos. En la práctica, los científicos a menudo buscan utilizar antecedentes “poco informativos” que tienen poca influencia en la distribución posterior, aunque incluso el término “poco informativo” puede resultar confuso, porque el previo es parte integral de un análisis bayesiano. El término también\(Pr(D)\) es una parte importante del teorema de Bayes, y puede calcularse como la probabilidad de obtener los datos integrados sobre las distribuciones previas de los parámetros:

\[Pr(D)=∫_HPr(H|D)Pr(H)dH \label{2.20}\]

Sin embargo,\(Pr(D)\) es constante al comparar el ajuste de diferentes modelos para un conjunto de datos dado y por lo tanto no tiene influencia en la selección de modelos bayesianos en la mayoría de las circunstancias (y todos los ejemplos de este libro).

En nuestro ejemplo de volteo de lagartos, podemos hacer un análisis en un marco bayesiano. Para el modelo 1, no hay parámetros libres. Debido a esto,\(Pr(H)=1\) y\(Pr(D|H)=P(D)\), para eso\(Pr(H|D)=1\). Esto puede parecer extraño pero lo que significa el resultado es que nuestros datos no influyen en la estructura del modelo. ¡No aprendemos nada de un modelo sin parámetros libres al recopilar datos!

Si consideramos el modelo 2 anterior, se debe estimar el parámetro p _H. Podemos establecer un previo uniforme entre 0 y 1 para p _H, de manera que f (p _H) =1 para todos los p _H en el intervalo [0,1]. También podemos escribir esto como “nuestro previo para\(p_h\) es U (0,1)”. Entonces:

\[ Pr(H|D) = \frac{Pr(D|H) \cdot Pr(H)}{Pr(D)} = \frac{P(H|p_H,N) f(p_H)}{\displaystyle \int_{0}^{1} P(H|p_H,N) f(p_h) dp_H} \label{2.21} \]

A continuación observamos que\(Pr(D|H)\) es la probabilidad de nuestros datos dado el modelo, el cual ya se establece anteriormente como Ecuación\ ref {2.2}. Al conectar esto a nuestra ecuación, tenemos:

\[ Pr(H|D) = \frac{\binom{N}{H} p_H^H (1-p_H)^{N-H}}{\displaystyle \int_{0}^{1} \binom{N}{H} p_H^H (1-p_H)^{N-H} dp_H} \label{2.22} \]

Esta fea ecuación en realidad se simplifica a una distribución beta, que se puede expresar de manera más simple como:

\[ Pr(H|D) = \frac{(N+1)!}{H!(N-H)!} p_H^H (1-p_H)^{N-H} \label{2.23} \]

Podemos comparar esta distribución posterior de nuestra estimación de parámetros, p _H, dados los datos, con nuestro uniforme previo (Figura 2.3). Si inspecciona esta parcela, verá que la distribución posterior es muy diferente a la anterior, es decir, los datos han cambiado nuestra visión de los valores que deben tomar los parámetros. Nuevamente, este resultado es cualitativamente consistente con los enfoques frecuentista y ML descritos anteriormente. En este caso, podemos ver desde la distribución posterior que podemos estar bastante seguros de que nuestro parámetro p _H no es 0.5.

Como puede ver en este ejemplo, el teorema de Bayes nos permite combinar nuestra creencia previa sobre los valores de los parámetros con la información de los datos para obtener una posterior. Estas distribuciones posteriores son muy fáciles de interpretar, ya que expresan la probabilidad de los parámetros del modelo dados nuestros datos. Sin embargo, esa claridad tiene el costo de requerir un previo explícito. Más adelante en el libro aprenderemos a utilizar esta característica de la estadística bayesiana para nuestro beneficio cuando realmente tenemos algún conocimiento previo sobre los valores de los parámetros.

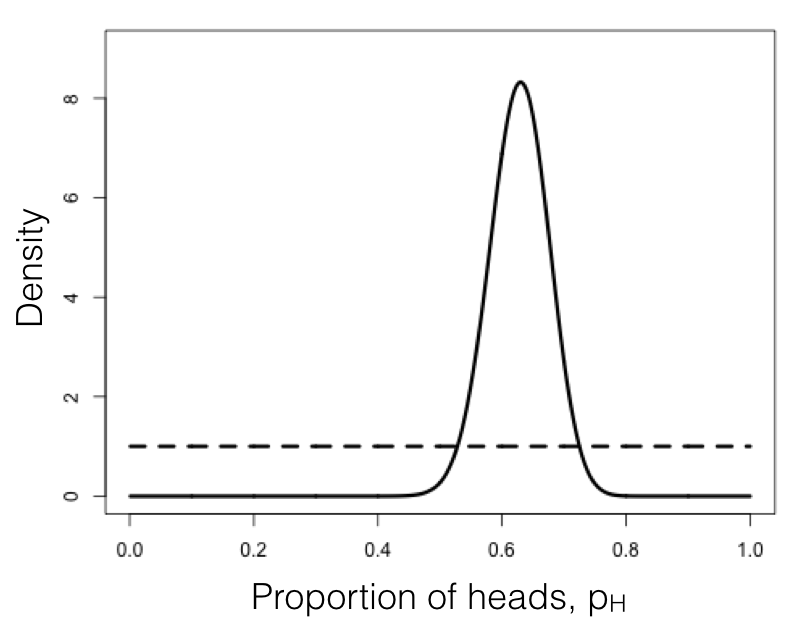
Figura 2.3. Distribuciones bayesianas anteriores (línea punteada) y posterior (línea continua) para volteo de lagartos. Imagen del autor, puede ser reutilizada bajo licencia CC-BY-4.0.

Sección 2.4b: MCMC bayesiano

La otra herramienta principal en la caja de herramientas de los métodos comparativos bayesianos es el uso de herramientas de cadena Markov Monte Carlo (MCMC) para calcular probabilidades posteriores. Las técnicas MCMC utilizan un algoritmo que utiliza una “cadena” de cálculos para muestrear la distribución posterior. MCMC requiere el cálculo de probabilidades pero no matemáticas complicadas (por ejemplo, integración de distribuciones de probabilidad, como en la Ecuación\ ref {2.22}, y así representa un enfoque más flexible para el cálculo bayesiano. Frecuentemente, las integrales en la Ecuación\ ref {2.21} son intratables, por lo que la forma más eficiente de adaptarse a los modelos bayesianos es mediante el uso de MCMC. Además, ¡configurar un MCMC es, en mi experiencia, más fácil de lo que la gente espera!

Un análisis MCMC requiere que uno construya y muestres de una cadena de Markov. Una cadena de Markov es un proceso aleatorio que cambia de un estado a otro con ciertas probabilidades que dependen únicamente del estado actual del sistema, y no de lo que ha venido antes. Un ejemplo sencillo de una cadena de Markov es el movimiento de una pieza de juego en el juego Chutes and Ladders; la posición de la pieza se mueve de un cuadrado a otro siguiendo las probabilidades dadas por los dados y la disposición del tablero de juego. El movimiento de la pieza desde cualquier cuadrado en el tablero no depende de cómo la pieza llegó a ese cuadrado.

Algunas cadenas de Markov tienen una distribución de equilibrio, que es una distribución de probabilidad estable de los estados del modelo después de que la cadena haya funcionado durante mucho tiempo. Para el análisis bayesiano, utilizamos una técnica llamada algoritmo Metropolis-Hasting para construir una cadena especial de Markov que tiene una distribución de equilibrio que es la misma que la distribución posterior bayesiana de nuestro modelo estadístico. Luego, usando una simulación aleatoria en esta cadena (esta es la cadena Markov Monte Carlo, MCMC), podemos muestrear de la distribución posterior de nuestro modelo.

En términos más simples: utilizamos un conjunto de reglas bien definidas. Estas reglas nos permiten caminar por el espacio de parámetros, en cada paso decidiendo si aceptar o rechazar el siguiente movimiento propuesto. Debido a algunas pruebas matemáticas que están más allá del alcance de este capítulo, estas reglas garantizan que eventualmente estaremos aceptando muestras de la distribución posterior bayesiana, que es lo que buscamos.

El siguiente algoritmo utiliza un algoritmo Metropolis-Hastings para realizar un análisis bayesiano de MCMC con un parámetro libre.

Algoritmo Metropolis-Hastings

1. Obtener un valor de parámetro inicial.
   • Muestrear un valor de parámetro inicial, p ₀, de la distribución anterior.
2. A partir de i = 1, proponer un nuevo parámetro para la generación i.
   • Dado el valor del parámetro actual, p, seleccione un nuevo valor de parámetro propuesto, p ′, utilizando la densidad propuesta Q (p ′| p).
3. Calcula tres proporciones.
   • a. El ratio de probabilidades anterior. Esta es la relación de la probabilidad de dibujar los valores de los parámetros p y p′ del anterior. \[R_{prior} = \frac{P(p')}{P(p)} \label{2.24}\]
   • b. La relación de densidad propuesta. Esta es la relación de probabilidad de propuestas que van de p a p ′ y a la inversa. A menudo, construimos a propósito una densidad de propuesta que es simétrica. Cuando hacemos eso, Q (p ′| p) = Q (p | p ′) y a ₂ = 1, simplificando los cálculos. \[R_{proposal} = \frac{Q(p'|p)}{Q(p|p')} \label{2.25}\]
   • c. La razón de verosimilitud. Esta es la relación de probabilidades de los datos dados los dos valores de parámetros diferentes. \[R_{likelihood} = \frac{L(p'|D)}{L(p|D)} = \frac{P(D|p')}{P(D|p)} \label{2.26}\]
4. Multiplicar. Encuentre el producto de las probabilidades anteriores, la relación de densidad propuesta y la razón de verosimilitud. \[R_{accept} = R_{prior} ⋅ R_{proposal} ⋅ R_{likelihood} \label{2.27}\]
5. Aceptar o rechazar. Dibuja un número aleatorio x a partir de una distribución uniforme entre 0 y 1. Si x < R _{a c c e p t}, acepte el valor propuesto de p′ (p _i = p ′); en caso contrario rechazar, y retener el valor actual p (p _i = p).
6. Repetir. Repita los pasos 2-5 una gran cantidad de veces.

Al llevar a cabo estos pasos, se obtiene un conjunto de valores de parámetros, p _i, donde i es de 1 al número total de generaciones en el MCMC. Por lo general, la cadena tiene un período de “burn-in” al principio. Este es el tiempo antes de que la cadena haya alcanzado una distribución estacionaria, y se puede observar cuando los valores de los parámetros muestran tendencias a través del tiempo y la probabilidad para los modelos aún no se ha estabilizado. Si elimina este periodo de “burn-in”, entonces, como se discutió anteriormente, cada paso de la cadena es una muestra de la distribución posterior. Podemos resumir las distribuciones posteriores de los parámetros del modelo de diversas maneras; por ejemplo, calculando medios, intervalos de confianza del 95% o histogramas.

Podemos aplicar este algoritmo a nuestro ejemplo de volteo de monedas. Consideraremos la misma distribución previa, U (0, 1), para el parámetro p. También definiremos una densidad de propuesta, Q (p ′| p) U (p −, p +). Es decir, sumaremos o restaremos un número pequeño (≤ 0.01) para generar valores propuestos de p ′ dado p.

Para iniciar el algoritmo, dibujamos un valor de p del anterior. Digamos con fines ilustrativos que el valor que dibujamos es de 0.60. Esto se convierte en nuestra estimación de parámetros actuales. Para el paso dos, proponemos un nuevo valor, p ′, a partir de nuestra distribución de propuestas. Podemos usar = 0.01 para que la distribución de la propuesta se convierta en U (0.59, 0.61). Supongamos que nuestro nuevo valor propuesto p ′=0.595.

Luego calculamos nuestras tres proporciones. Aquí las cosas son más simples de lo que podrías haber esperado por dos razones. Primero, recordemos que nuestra distribución de probabilidad previa es U (0, 1). La densidad de esta distribución es una constante (1.0) para todos los valores de p y p′. Debido a esto, el ratio de probabilidades anterior para este ejemplo es siempre:

\[ R_{prior} = \frac{P(p')}{P(p)} = \frac{1}{1} = 1 \label{2.28}\]

Del mismo modo, debido a que nuestra distribución propuesta es simétrica, Q (p ′| p) = Q (p | p ′) y R _{p r o p o s a l} = 1. Eso quiere decir que solo necesitamos calcular la razón de verosimilitud, R _{l i k e l i h o o d} para p y p ′. Podemos hacer esto al conectar nuestros valores para p (o p ′) en la Ecuación\ ref {2.2}:

\[ P(D|p) = {N \choose H} p^H (1-p)^{N-H} = {100 \choose 63} 0.6^63 (1-0.6)^{100-63} = 0.068 \label{2.29} \]

Asimismo,

\[ P(D|p') = {N \choose H} p'^H (1-p')^{N-H} = {100 \choose 63} 0.595^63 (1-0.595)^{100-63} = 0.064 \label{2.30}\]

La razón de verosimilitud es entonces:

\[ R_{likelihood} = \frac{P(D|p')}{P(D|p)} = \frac{0.064}{0.068} = 0.94 \label{2.31}\]

Ahora podemos calcular R _{a c c e p t} = R _{p r i o r} ⋅ R _{p r o p o s a l} ⋅ R _{l i k e l i h o o d} = 1 ⋅ 1 ⋅ 0.94 = 0.94. A continuación elegimos un número aleatorio entre 0 y 1 — digamos que dibujamos x = 0.34. Entonces notamos que nuestro número aleatorio x es menor o igual a R _{a c c e p t}, por lo que aceptamos el valor propuesto de p ′. Si el número aleatorio que dibujamos fuera mayor a 0.94, rechazaríamos el valor propuesto, y mantendríamos nuestro valor de parámetro original p = 0.60 entrando en la siguiente generación.

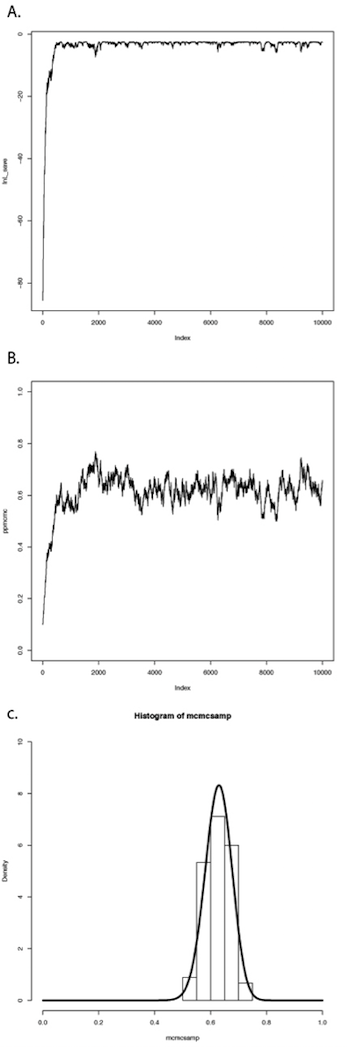
Si repetimos este procedimiento un gran número de veces, obtendremos una larga cadena de valores de p. Se pueden ver los resultados de dicha ejecución en la Figura 2.4. En el panel A, he trazado las probabilidades para cada valor sucesivo de p. Se puede ver que las probabilidades aumentan para las primeras ~1000 generaciones más o menos, luego alcanzan una meseta alrededor de l n L = −3. El Panel B muestra una gráfica de los valores de p, los cuales convergen rápidamente a una distribución estable alrededor de p = 0.63. También podemos trazar un histograma de estas estimaciones posteriores de p. En el panel C, lo he hecho —pero con un giro. Debido a que el algoritmo MCMC crea una serie de estimaciones de parámetros, estos números muestran autocorrelación, es decir, cada estimación es similar a las estimaciones que vienen justo antes y justo después. Esta autocorrelación puede causar problemas para el análisis de datos. La solución más sencilla es submuestrear estos valores, escogiendo solo, digamos, un valor cada 100 generaciones. Eso es lo que he hecho en el histograma en el panel C. Este panel también incluye la distribución analítica posterior que calculamos anteriormente — ¡fíjate lo bien que hizo nuestro algoritmo Metropolis-Hastings en la reconstrucción de esta distribución! Para los métodos comparativos en general, las distribuciones analíticas posteriores son difíciles o imposibles de construir, por lo que la aproximación usando MCMC es muy común.

Figura 2.4. MCMC bayesiano de ejemplo de volteo de lagarto. Imagen del autor, puede ser reutilizada bajo licencia CC-BY-4.0.

Este sencillo ejemplo pasa por alto algunos de los detalles de los algoritmos MCMC, pero entraremos en esos detalles más adelante, y hay muchos otros libros que tratan este tema con gran profundidad (por ejemplo, Christensen et al. 2010). El punto es que podemos resolver algunos de los desafíos que implica la estadística bayesiana utilizando “trucos” numéricos como MCMC, que explotan el poder de las computadoras modernas para adaptarse a modelos y estimar parámetros del modelo.

Sección 2.4c: Factores Bayes

Ahora que sabemos usar los datos y un previo para calcular una distribución posterior, podemos pasar al tema de la selección de modelos bayesianos. Ya aprendimos un método general para la selección de modelos usando AIC. También podemos hacer selección de modelos en un marco bayesiano. La forma más sencilla es calcular y luego comparar las probabilidades posteriores para un conjunto de modelos bajo consideración. Esto se puede hacer calculando los factores Bayes:

\[ B_{12} = \frac{Pr(D|H_1)}{Pr(D|H_2)} \label{2.32}\]

Los factores Bayes son proporciones de las probabilidades marginales P (D | H) de dos modelos competidores. Representan la probabilidad de los datos promediados sobre la distribución posterior de las estimaciones de parámetros. Es importante señalar que estas probabilidades marginales son diferentes de las probabilidades utilizadas anteriormente para la comparación de modelos A I C de manera importante. Con A I C y otras pruebas relacionadas, calculamos las probabilidades para un modelo dado y un conjunto particular de valores de parámetros —en el ejemplo de volteo de monedas, la probabilidad para el modelo 2 cuando p _H = 0.63. Por el contrario, las probabilidades marginales de los factores Bayes dan la probabilidad de que los datos promedien sobre todos los valores de parámetros posibles para un modelo, ponderados por su probabilidad previa.

Debido al uso de probabilidades marginales, el factor Bayes nos permite hacer la selección de modelos de una manera que da cuenta de la incertidumbre en nuestras estimaciones de parámetros, de nuevo, sin embargo, a costa de requerir probabilidades previas explícitas para todos los parámetros del modelo. Dichas comparaciones pueden ser bastante diferentes de las pruebas de razón de verosimilitud o las comparaciones de puntuaciones A I C _c. Los factores Bayes representan comparaciones de modelos que se integran sobre todos los valores de parámetros posibles en lugar de comparar el ajuste de los modelos solo en los valores de parámetros que mejor se ajustan a los datos. Es decir, las puntuaciones A I C _c comparan el ajuste de dos modelos dados valores estimados particulares para todos los parámetros en cada uno de los modelos. Por el contrario, los factores de Bayes hacen una comparación entre dos modelos que da cuenta de la incertidumbre en sus estimaciones de parámetros. Esto marcará la mayor diferencia cuando algunos parámetros de uno o ambos modelos tengan una incertidumbre relativamente amplia. Si todos los parámetros se pueden estimar con precisión, los resultados de ambos enfoques deben ser similares.

El cálculo de los factores de Bayes puede ser bastante complicado, requiriendo integración a través de distribuciones de probabilidad. En el caso de nuestro problema de volteo de monedas, ya lo hemos hecho para obtener la distribución beta en la Ecuación\ ref {2.22. Luego podemos calcular los factores Bayes para comparar el ajuste de dos modelos competidores. Comparemos los dos modelos para volteo de monedas considerados anteriormente: el modelo 1, donde p _H = 0.5, y el modelo 2, donde p _H = 0.63. Entonces:

\[ \begin{array}{lcl} Pr(D|H_1) &=& \binom{100}{63} 0.5^{0.63} (1-0.5)^{100-63} \\\ &=& 0.00270 \\\ Pr(D|H_2) &=& \int_{p=0}^{1} \binom{100}{63} p^{63} (1-p)^{100-63} \\\ &=& \binom{100}{63} \beta (38,64) \\\ &=& 0.0099 \\\ B_{12} &=& \frac{0.0099}{0.00270} \\\ &=& 3.67 \\\ \end{array} \label{2.33}\]

En el ejemplo anterior, β (x, y) es la función Beta. Nuestros cálculos muestran que el factor Bayes es de 3.67 a favor del modelo 2 comparado con el modelo 1. Esto se interpreta típicamente como evidencia sustancial (pero no decisiva) a favor del modelo 2. Nuevamente, podemos estar razonablemente seguros de que nuestro lagarto no es un flipper justo.

En el ejemplo de volteo de lagarto podemos calcular los factores Bayes exactamente porque conocemos la solución a la integral en la Ecuación\ ref {2.33. Sin embargo, si no sabemos cómo resolver esta ecuación (una situación típica en métodos comparativos), aún podemos aproximar los factores de Bayes a partir de nuestras ejecuciones MCMC. Los métodos para ello, incluyendo el muestreo de arrogancia y los modelos de escalón (Xie et al. 2011; Perrakis et al. 2014), son complejos y están fuera del alcance de este libro. Sin embargo, un método común para aproximar los Factores de Bayes implica calcular la media armónica de las probabilidades sobre la cadena MCMC para cada modelo. La relación de estas dos probabilidades se utiliza entonces como aproximación del factor Bayes (Newton y Raftery 1994). Desafortunadamente, este método es extremadamente poco confiable, y probablemente nunca debería usarse (ver Neal 2008 para más detalles).