3.2: Propiedades del Movimiento Browniano
- Page ID
- 54159
Podemos utilizar el movimiento browniano para modelar la evolución de un rasgo continuamente valorado a través del tiempo. El movimiento browniano es un ejemplo de un modelo de “caminata aleatoria” porque el valor del rasgo cambia aleatoriamente, tanto en dirección como en distancia, en cualquier intervalo de tiempo. El proceso estadístico del movimiento browniano se inventó originalmente para describir el movimiento de partículas suspendidas en un fluido. Para mí esto es un poco difícil de imaginar, pero la lógica se aplica igualmente bien al movimiento de una pelota grande sobre una multitud en un estadio. Cuando la pelota está sobre la multitud, la gente la empuja desde muchas direcciones. La suma de estas muchas fuerzas pequeñas determina el movimiento de la pelota. Nuevamente, el movimiento de la pelota se puede modelar usando el movimiento browniano 1.
La idea central de este ejemplo es que el movimiento del objeto se debe a la suma de un gran número de fuerzas aleatorias muy pequeñas. Esta idea es una parte clave de los modelos biológicos de evolución bajo el movimiento browniano. Cabe mencionar que aunque el movimiento browniano implica un cambio que tiene un fuerte componente aleatorio, es incorrecto equiparar los modelos de movimiento browniano con modelos de deriva genética pura (como se explica con más detalle a continuación).
El movimiento browniano es un modelo popular en biología comparada porque captura la forma en que los rasgos pueden evolucionar bajo una gama razonablemente amplia de escenarios. Sin embargo, quizás la razón principal del dominio del movimiento browniano como modelo es que tiene algunas propiedades estadísticas muy convenientes que permiten análisis y cálculos relativamente simples en árboles. Utilizaré algunas simulaciones simples para mostrar cómo se comporta el modelo de movimiento browniano. Luego enumeraré las tres propiedades estadísticas críticas del movimiento browniano y explicaré cómo podemos usar estas propiedades para aplicar modelos de movimiento browniano a árboles comparativos filogenéticos.
Cuando modelamos la evolución usando el movimiento browniano, normalmente estamos discutiendo la dinámica del valor medio del carácter, que denotaremos como $\ bar {z} $, en una población. Es decir, imaginamos que se puede medir una muestra de los individuos en una población y estimar el valor promedio promedio del rasgo. Denotaremos el valor de rasgo medio en algún momento t como $\ bar {z} (t) $. Podemos modelar el valor medio del rasgo a través del tiempo con un proceso de movimiento browniano.
Los modelos de movimiento browniano pueden describirse completamente por dos parámetros. El primero es el valor inicial del rasgo medio poblacional, $\ bar {z} (0) $. Este es el valor de rasgo medio que se ve en la población ancestral al inicio de la simulación, antes de que ocurra cualquier cambio de rasgo. El segundo parámetro del movimiento browniano es el parámetro de tasa evolutiva, σ 2. Este parámetro determina qué tan rápido los rasgos caminarán aleatoriamente a través del tiempo.
En el núcleo del movimiento browniano se encuentra la distribución normal. Es posible que sepas que una distribución normal puede ser descrita por dos parámetros, la media y la varianza. Bajo el movimiento browniano, los cambios en los valores de rasgo a lo largo de cualquier intervalo de tiempo siempre se extraen de una distribución normal con media 0 y varianza proporcional al producto de la tasa de evolución y la duración del tiempo (varianza = σ 2 t). Como mostraré más adelante, podemos simular el cambio bajo el modelo de movimiento browniano dibujando a partir de distribuciones normales. Otra forma de decir esto de manera más simple es que siempre podemos describir cuánto cambio esperar bajo el movimiento browniano usando distribuciones normales. Estas distribuciones normales para los cambios esperados tienen una media de cero y se hacen más amplias a medida que el intervalo de tiempo que consideramos se alarga.
Algunas simulaciones ilustrarán el comportamiento del movimiento browniano. La Figura 3.1 muestra conjuntos de movimiento browniano ejecutados en tres periodos de tiempo diferentes (t = 100, 500 y 1000) con el mismo valor inicial $\ bar {z} (0) = 0$ y el parámetro de tasa σ 2 = 1. Cada panel de la figura muestra 100 simulaciones del proceso durante ese periodo de tiempo. Se puede ver que los valores de punta parecen distribuciones normales. Además, la varianza entre series separadas del proceso aumenta linealmente con el tiempo. Esta varianza entre corridas es mayor en los intervalos de tiempo más largos. Es esta varianza, la variación entre muchas corridas independientes del mismo proceso evolutivo, la que consideraremos a lo largo de la siguiente sección.
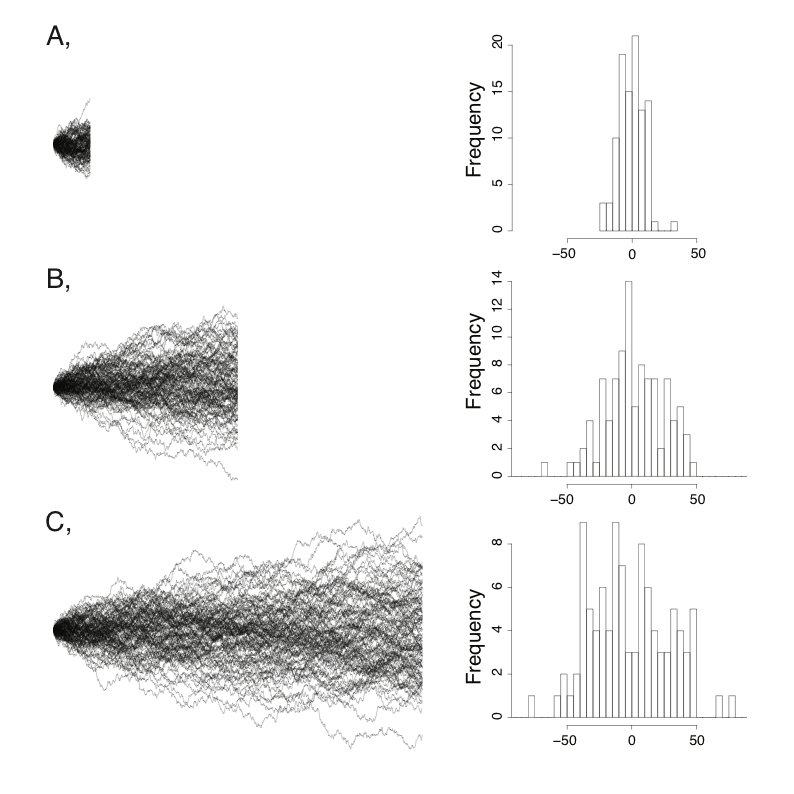
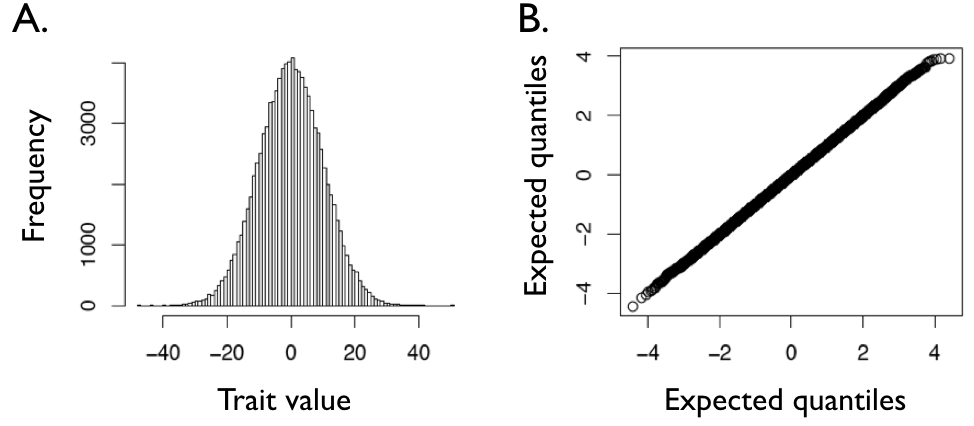
Imagina que ejecutamos un proceso de movimiento browniano en un intervalo de tiempo dado muchas veces, y guardamos los valores de rasgo al final de cada una de estas simulaciones. Entonces podemos crear una distribución estadística de estos estados de carácter. Puede que no sea obvio a partir de la figura 3.1, pero las distribuciones de posibles estados de carácter en cualquier momento de una caminata browniana es normal. Esto se ilustra en la figura 3.2, que muestra la distribución de rasgos a partir de 100,000 simulaciones con σ 2 = 1 y t = 100. Los caracteres de punta de todas estas simulaciones siguen una distribución normal con una media igual al valor inicial, $\ bar {z} (0) = 0$, y una varianza de σ 2 t = 100.
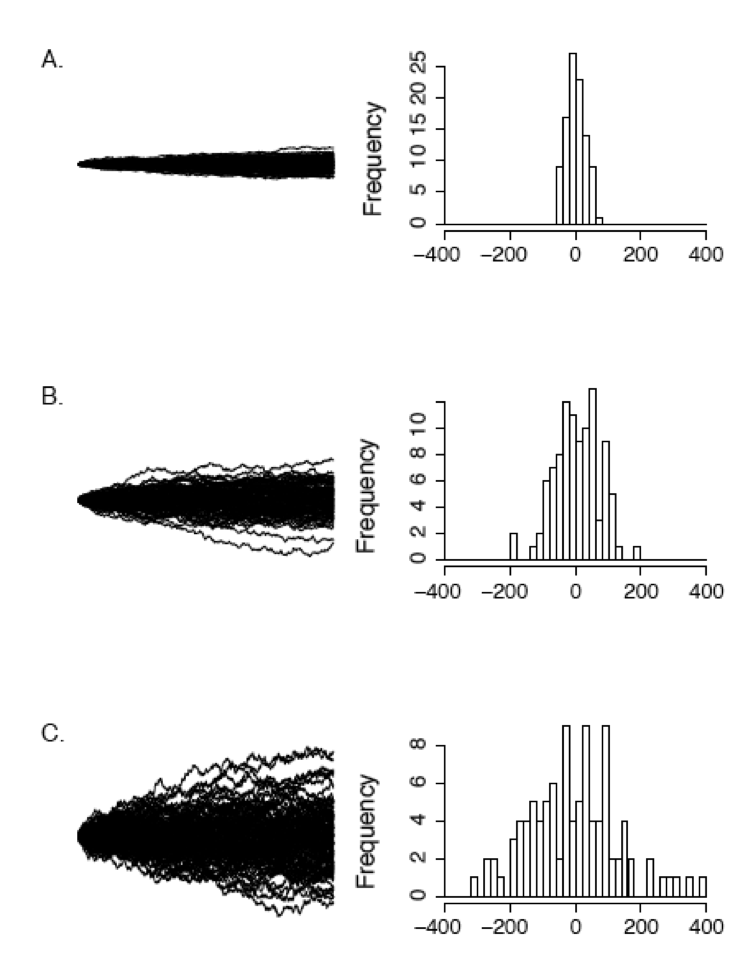
La Figura 3.3 muestra cómo el parámetro de tasa σ 2 afecta a la tasa de propagación de las caminatas brownianas. Los paneles muestran conjuntos de 100 simulaciones de movimiento browniano ejecutadas sobre 1000 unidades de tiempo para σ 2 = 1 (Panel A), σ 2 = 5 (Panel B) y σ 2 = 25 (Panel C). Puede ver que las simulaciones con un parámetro de tasa más alta crean una mayor dispersión de los valores de rasgos entre las simulaciones durante la misma cantidad de tiempo.
Si dejamos\( \bar{z}(t)\) ser el valor de nuestro personaje en el tiempo t, entonces podemos derivar tres propiedades principales del movimiento browniano. Voy a enumerar los tres, luego explicaré cada uno por turno.
- \(E[\bar{z}(t)] = \bar{z}(0)\)
- Cada intervalo sucesivo de la “caminata” es independiente
- \(\bar{z}(t) \sim N(\bar{z}(0),\sigma^2 t)\)
En primer lugar,\( E[\bar{z}(t)] = \bar{z}(0)\). Esto significa que el valor esperado del carácter en cualquier momento t es igual al valor del carácter en el tiempo cero. Aquí el valor esperado se refiere a la media de\( \bar{z}(t)\) más de muchas réplicas. El significado intuitivo de esta ecuación es que el movimiento browniano no tiene “tendencias”, y deambula por igual tanto en direcciones positivas como negativas. Si tomas la media de un gran número de simulaciones de movimiento browniano en cualquier intervalo de tiempo, es probable que obtengas un valor cercano a $\ bar {z} (0) $; a medida que aumentes el tamaño de la muestra, esta media tenderá a acercarse cada vez más\( \bar{z}(0)\).
Segundo, cada intervalo sucesivo de la “caminata” es independiente. El movimiento browniano es un proceso en tiempo continuo, por lo que el tiempo no tiene “pasos” discretos. Sin embargo, si muestrea el proceso desde el tiempo 0 hasta el tiempo t, y luego nuevamente en el tiempo t + Δ t, el cambio que se produzca a lo largo de estos dos intervalos será independiente el uno del otro. Esto es cierto para dos intervalos no superpuestos muestreados de una caminata browniana. Cabe señalar que sólo los cambios son independientes, y que el valor de la caminata en el tiempo t + Δ t — que podemos escribir como $\ bar {z} (t+\ Delta t) $ - no es independiente del valor de la caminata en el tiempo t,\( \bar{z}(t)\). Pero las diferencias entre pasos sucesivos [e.g\(\bar{z}(t)-\bar{z}(0)\) y\(\bar{z}(t+\Delta t) - \bar{z}(t)\)] son independientes entre sí y de\( \bar{z}(0)\).
Finalmente,\( \bar{z}(t) \sim N(\bar{z}(0),\sigma^2 t)\) .Es decir, el valor de\( \bar{z}(t)\) se extrae de una distribución normal con media\( \bar{z}(0)\) y varianza σ 2 t. Como señalamos anteriormente, el parámetro σ 2 es importante para los modelos de movimiento brownianos, ya que describe la velocidad a la que el proceso deambula por el espacio de rasgos. La varianza general del proceso es esa tasa multiplicada por la cantidad de tiempo que ha transcurrido.


