3.4: Movimiento browniano en un árbol filogenético
- Page ID
- 54158
Podemos usar las propiedades básicas del modelo de movimiento browniano para averiguar qué sucederá cuando los personajes evolucionen bajo este modelo en las ramas de un árbol filogenético. Primero, considere la evolución a lo largo de una sola rama con longitud t 1 (Figura 3.4A). En este caso, podemos modelar movimiento browniano simple a lo largo del tiempo t 1 y denotar el valor inicial como\(\bar{z}(0)\). Si evolucionamos con algún parámetro de tasa σ B 2, entonces:
\[ E[\bar{z}(t)] \sim N(\bar{z}(0), \sigma_B^2 t_1) \label{3.17} \]
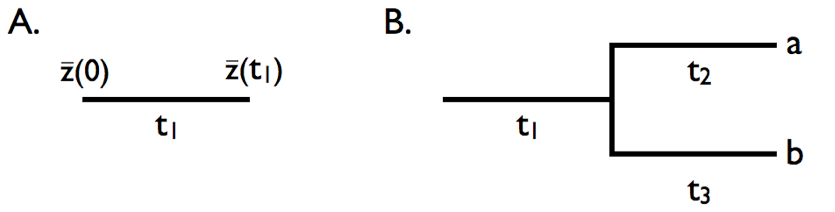
Ahora considere una pequeña sección de un árbol filogenético que incluye dos especies y una rama ancestral del tallo (Figura 3.4B). Supongamos que un personaje evoluciona en ese árbol bajo el movimiento browniano, nuevamente con el valor inicial\(\bar{z}(0)\) y el parámetro de tasa σ B 2. Primero considere la especie a. el rasgo medio en que la especie\(\bar{x}_a\) evoluciona bajo el movimiento browniano del antepasado a la especie a en un tiempo total de t 1 + t 2. Así,
\[ \bar{x}_a \sim N[\bar{z}(0), \sigma_B^2 (t_1+t_2)] \label{3.18}\]
De manera similar para la especie b, durante un tiempo total de t 1 + t 3
\[ \bar{x}_b \sim N[\bar{z}(0),\sigma_B^2 (t_1+t_3)] \label{3.19} \]
Sin embargo,\( \bar{x}_a\) y no\( \bar{x}_b\) son independientes entre sí. En cambio, las dos especies comparten una rama en común (rama 1). Cada valor de rasgo de punta se puede considerar como un valor ancestral más la suma de dos cambios evolutivos: uno (de la rama 1) que se comparte entre las dos especies y otro que es único (rama 2 para la especie a y rama 3 para la especie b). En este caso, los valores de rasgos medios\( \bar{x}_a\) y\( \bar{x}_b\) compartirán similitud debido a su historia evolutiva compartida. Podemos describir esta similitud calculando la covarianza entre los rasgos de las especies a y b. Observamos que:
\[ \begin{array}{lcr} \bar{x}_a = \Delta \bar{x}_1 + \Delta \bar{x}_2\\ \bar{x}_b = \Delta \bar{x}_1 + \Delta \bar{x}_3\\ \end{array} \label{3.20} \]
Donde\(\Delta \bar{x}_1\)\(\Delta \bar{x}_2\), y\(\Delta \bar{x}_3\) representan la evolución a lo largo de las tres ramas del árbol, están todas normalmente distribuidas con cero medio y varianzas σ 2 t 1, σ 2 t 2 y σ 2 t 3, respectivamente. \(\bar{x}_a\)y\(\bar{x}_b\) son sumas de variables aleatorias normales y son ellas mismas normales. La covarianza de estos dos términos es simplemente la varianza de su término compartido:
\[ cov(\bar{x}_a,\bar{x}_b)=var(\Delta \bar{x}_1)=\sigma_B^2 t_1 \label{3.21} \]
También vale la pena señalar que podemos describir los valores de rasgo para las dos especies como un solo sorteo a partir de una distribución normal multivariada. Cada rasgo tiene el mismo valor esperado\(\bar{z}(0)\), y los dos rasgos tienen una matriz de varianza-covarianza:
\[ \begin{bmatrix} \sigma^2 (t_1 + t_2) & \sigma^2 t_1 \\ \sigma^2 t_1 & \sigma^2 (t_1 + t_3) \\ \end{bmatrix} = \sigma^2 \begin{bmatrix} t_1 + t_2 & t_1 \\ t_1 & t_1 + t_3 \\ \end{bmatrix} = \sigma^2 \mathbf{C} \label{3.22} \]
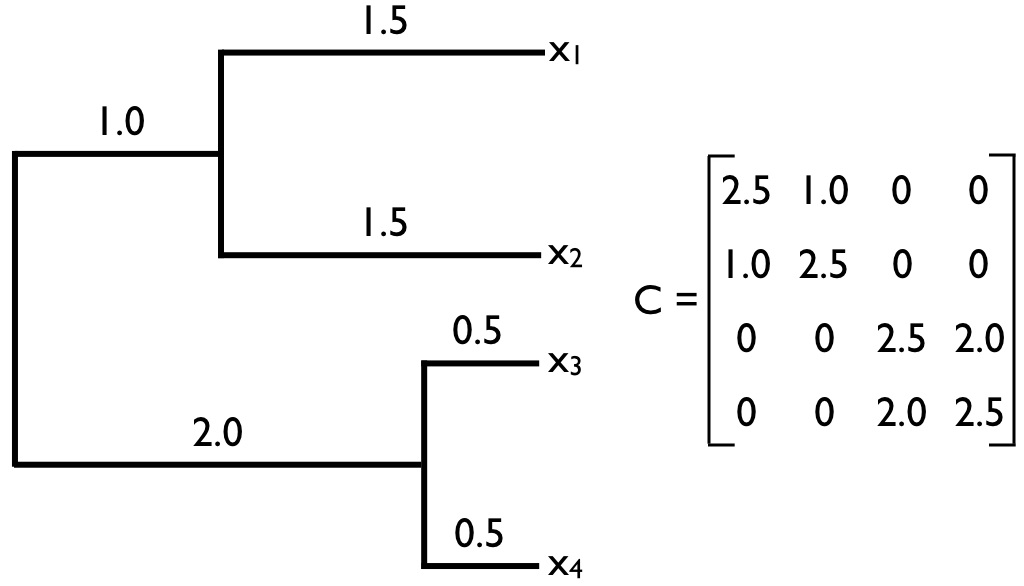
La matriz C en la Ecuación\ ref {3.22} se encuentra comúnmente en biología comparada, y volverá a aparecer en este libro. Llamaremos a esta matriz la matriz de varianza-covarianza filogenética. Esta matriz tiene una estructura especial. Para árboles filogenéticos con n especies, esta es una matriz n × n, con cada fila y columna correspondiente a uno de los n taxones del árbol. A lo largo de la diagonal se encuentran las distancias totales de cada taxón desde la raíz del árbol, mientras que los elementos fuera de la diagonal son las longitudes totales de rama compartidas por pares particulares de taxones. Por ejemplo, C (1, 2) y C (2, 1) —que son iguales porque la matriz C es siempre simétrica— es la longitud del camino filogenético compartido entre las especies en la primera fila —aquí, la especie a- y la especie en la segunda fila— aquí, la especie b. Bajo el movimiento browniano, estas las longitudes de ruta compartida son proporcionales a las covarianzas filogenéticas de los valores de los rasgos. Un ejemplo completo de una matriz filogenética varianza-covarianza para un árbol pequeño se muestra en la Figura 3.5. Esta distribución normal multivariada describe completamente la distribución estadística esperada de rasgos en las puntas de un árbol filogenético si los rasgos evolucionan de acuerdo con un modelo de movimiento browniano.