4.2: Estimación de tasas mediante contrastes independientes

La información requerida para estimar las tasas evolutivas se resume de manera eficiente en el método filogenético comparativo temprano (pero aún útil) de contrastes independientes (Felsenstein 1985). Los contrastes independientes resumen la cantidad de cambio de carácter en cada nodo del árbol y se pueden usar para estimar la tasa de cambio de carácter a través de una filogenia. También existe una relación matemática simple entre los contrastes y las estimaciones de tasa de máxima verosimilitud que discutiré a continuación.

Podemos entender la idea básica detrás de los contrastes independientes si pensamos en las ramas del árbol filogenético como las “vías” históricas de la evolución. Cada rama del árbol representa un linaje que estuvo vivo en algún momento de la historia de la Tierra, y durante ese tiempo experimentó cierta cantidad de cambio evolutivo. Podemos imaginar intentar medir ese cambio inicialmente comparando taxones hermanos. Podemos comparar los valores de los rasgos de los dos taxones hermanos encontrando la diferencia en sus valores de rasgo, y luego compararlo con la cantidad total de tiempo que han tenido para evolucionar esa diferencia. Al hacer esto para todos los taxones hermanos del árbol, obtendremos una estimación de la tasa promedio de evolución de caracteres (4.1A). Pero, ¿qué pasa con los nodos más profundos en el árbol? Podríamos usar otras parejas de especies no hermanas, pero luego estaríamos contando algunas ramas en el árbol de la vida más de una vez (Figura 4.1B). En su lugar, usamos un “algoritmo de poda” (Felsenstein 1985, Felsenstein (2004)) cortando pares de taxones hermanos para crear un árbol más pequeño (Figura 4.1C). Eventualmente, todos los nodos en el árbol serán recortados — y el algoritmo terminará. Los contrastes independientes proporcionan una manera de generalizar el enfoque de comparación de taxones hermanos para que podamos cuantificar la tasa de evolución a lo largo de todo el árbol.

Figura 4.1. Algoritmo de poda que se puede utilizar para identificar cinco contrastes independientes para un árbol con seis especies (siguiendo a Felsenstein 1985). El orden numerado en esta figura es sólo una de varias posibilidades que funcionan; también se puede podar el árbol en el orden 1, 2, 4, 3, 5 y obtener resultados idénticos. Imagen del autor, puede ser reutilizada bajo licencia CC-BY-4.0.

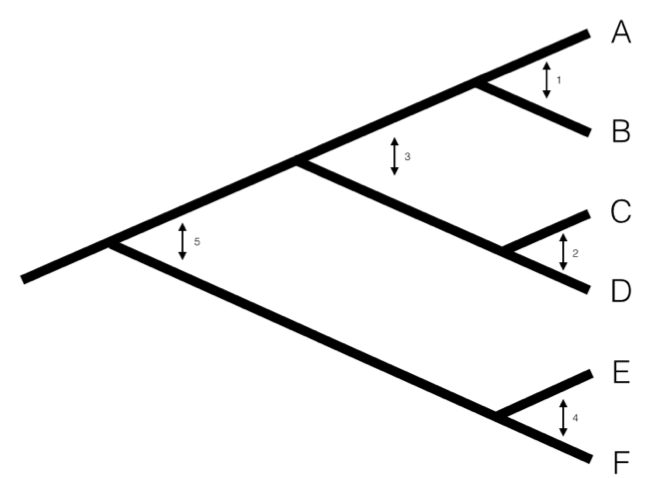
Un algoritmo más preciso que describe cómo se calculan los contrastes filogenéticos independientes (PIC) se proporciona en el recuadro 4.2, a continuación (de Felsenstein 1985). Cada contraste puede describirse como una estimación de la dirección y cantidad de cambio evolutivo a través de los nodos en el árbol. Los PIC se calculan desde las puntas del árbol hacia la raíz, como diferencias entre los valores de rasgo en las puntas del árbol y/o los valores promedio calculados en los nodos internos. Las diferencias en sí mismas a veces se llaman “contrastes crudos” (Felsenstein 1985). Estos contrastes brutos serán todos estadísticamente independientes entre sí bajo una amplia gama de modelos evolutivos. De hecho, siempre y cuando cada linaje en un árbol filogenético evolucione independientemente de cada otro linaje, independientemente del modelo evolutivo, los contrastes crudos serán independientes entre sí. Sin embargo, las personas casi nunca usan contrastes crudos porque no están distribuidos de manera idéntica; cada contraste crudo tiene una distribución esperada diferente que depende del modelo de evolución y las longitudes de rama del árbol. En particular, bajo movimiento browniano esperamos más cambios en ramas más largas del árbol. Felsenstein (1985) dividió los contrastes brutos por su desviación estándar esperada bajo un modelo de movimiento browniano, resultando en contrastes estandarizados. Estos contrastes estandarizados son, bajo un modelo BM, tanto independientes como idénticamente distribuidos, y pueden ser utilizados en una variedad de pruebas estadísticas. Obsérvese que debemos asumir un modelo de movimiento browniano para estandarizar los contrastes; los resultados derivados de los contrastes, entonces, dependen de esta suposición del movimiento browniano.

Recuadro 4.2: Algoritmo para Contrastes Filogenéticos Independientes

Se pueden calcular los PIC usando el algoritmo de Felsenstein (1985). Reproduzco este algoritmo a continuación. Ten en cuenta que este es un algoritmo iterativo: repites los cinco pasos a continuación una vez por cada contraste, o n − 1 veces en todo el árbol (ver Figura 4.1C como ejemplo).

1. Encuentra dos consejos sobre la filogenia que son adyacentes (digamos nodos i y j) y tienen un ancestro común, digamos nodo k. Tenga en cuenta que la elección de qué nodo es i y cuál es j es arbitraria. Como verás, ¡tendremos que dar cuenta de esta propiedad de “dirección arbitraria” de los PIC en cualquier análisis donde los utilicemos para hacer análisis certian!

2. Calcule el contraste sin procesar, la diferencia entre sus dos valores de punta:\[c_{ij} = x_i − x_j \label{4.1}\]

• Bajo un modelo de movimiento browniano, c _{i j} tiene expectativa cero y varianza proporcional a v _i + v _j.

3. Calcular el contraste estandarizado dividiendo el contraste crudo por su varianza\ [s_ {ij} =\ frac {c_ {ij}} {v_i + v_j} =\ frac {x_i - x_j} {v_i + v_j}\ label {4.2}\ [

• Bajo un modelo de movimiento browniano, este contraste sigue una distribución normal con cero medio y varianza igual al parámetro de velocidad de movimiento browniano σ ².

4. Retire las dos puntas del árbol, dejando atrás solo al ancestro k, que ahora se convierte en una punta. Asignarle el valor del carácter:\ [x_k =\ frac {(1/v_i) x_i+ (1/v_j) x_j} {1/v_1+1/v_j}\ label {4.3}\ [
   • Cabe señalar que x _k es un promedio ponderado de x _i y x _j, pero no representa una reconstrucción del estado ancestral, ya que el valor solo está influenciado por especies que descienden directamente de ese nodo y no de otros parientes.
5. Alargar la rama debajo del nodo k aumentando su longitud de v _k a v _k + v _i v _j/(v _i + v _j). Esto da cuenta de la incertidumbre en la asignación de un valor a x _k.

Como se mencionó anteriormente, podemos aplicar el algoritmo de contrastes independientes para aprender algo sobre las tasas de evolución del tamaño corporal en mamíferos. Tenemos un árbol filogenético con longitudes de ramas así como estimaciones de masa corporal para 49 especies (Figura 4.2). Si transformamos masa y luego aplicamos el método anterior a nuestros datos sobre el tamaño corporal de los mamíferos, obtenemos un conjunto de 48 contrastes estandarizados. Un histograma de estos contrastes se muestra como Figura 4.2 (datos de Garland 1992).

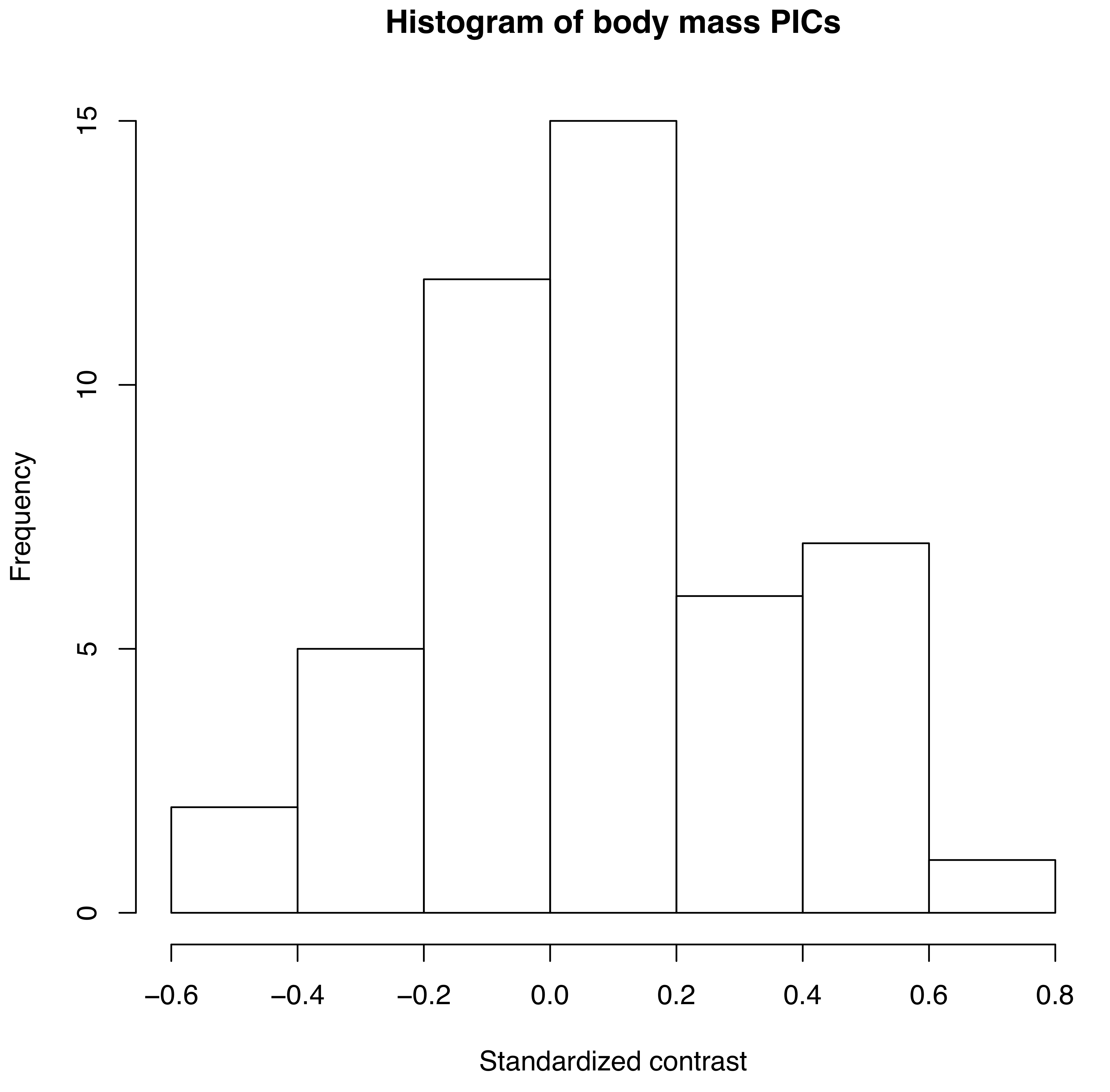
Figura 4.2. Histograma de PIC para la masa corporal de mamíferos transformados por lin en un árbol filogenético con longitudes de rama en millones de años (datos de Garland 1992). Imagen del autor, puede ser reutilizada bajo licencia CC-BY-4.0.

Tenga en cuenta que cada contraste es una cantidad de cambio, x _i − x _j, dividido por una longitud de rama, v _i + v _j, que es una medida del tiempo. Así, los PICs de un solo rasgo pueden ser utilizados para estimar σ ², la tasa de evolución bajo un modelo browniano. La estimación PIC de la tasa evolutiva es:

\[ \hat{\sigma}_{PIC}^2 = \frac{\sum{s_{ij}^2}}{n-1} \label{4.4}\]

Es decir, la estimación PIC de la tasa evolutiva es el promedio de los contrastes n − 1 al cuadrado. Esta suma se toma sobre todos los s _{i j}, el contraste independiente estandarizado en todos los (i, j) pares de ramas hermanas en el árbol filogenético. Para un árbol completamente bifurcado con n puntas, hay exactamente n − 1 de esos pares. Si eres estadísticamente inteligente, podrías notar que esta fórmula se parece un poco a una varianza. De hecho, si afirmamos que los contrastes tienen una media de 0 (que deben porque el movimiento browniano no tiene tendencias generales), entonces esta es una fórmula para estimar la varianza de los contrastes.

Si calculamos la suma media de los contrastes cuadrados para los datos de masa corporal del mamífero, obtenemos una estimación de la tasa de $\ hat {\ sigma} _ {PIC} ^2$ = 0.09. Podemos poner esto en palabras: si simulamos la evolución de la masa corporal de mamíferos bajo este modelo, esperaríamos que la varianza entre series replicadas aumentara en 0.09 por millón de años. O, en términos más concretos, si pensamos en dos linajes divergentes entre sí durante un millón de años, podemos extraer cambios en la masa corporal de ambos a partir de una distribución normal con una varianza de 0.09. Su diferencia, entonces, que es la cantidad de divergencia esperada, será normal con una varianza de 2 ⋅ 0.09 = 0.18. Así, con 95% de confianza, podemos esperar que las dos especies difieran al máximo por dos desviaciones estándar de esta distribución, $2\ cdot\ sqrt {0.18} = 0.85$. Dado que estamos en una escala logarítmica, esta cantidad de cambio corresponde a un factor de e ^2.68 = 2.3, lo que significa que una especie comúnmente será aproximadamente el doble de grande (o pequeña) que la otra después de solo un millón de años.