4.3: Estimación de tasas usando máxima verosimilitud
- Page ID
- 53772
También podemos estimar la tasa evolutiva encontrando los valores de los parámetros de máxima verosimilitud para un modelo de movimiento browniano que se ajuste a nuestros datos. Recordemos que los valores de los parámetros ML son aquellos que maximizan la probabilidad de los datos dado nuestro modelo (ver Capítulo 2).
Ya sabemos que bajo un modelo de movimiento browniano, los estados de carácter de punta se extraen de una distribución normal multivariada con una matriz de varianza-covarianza, C, que se calcula con base en las longitudes de rama y topología del árbol filogenético (ver Capítulo 3). Podemos calcular la probabilidad de obtener los datos bajo nuestro modelo de movimiento browniano usando una fórmula estándar para la probabilidad de dibujar a partir de una distribución normal multivariada:
\[ L(\mathbf{x} | \bar{z}(0), \sigma^2, \mathbf{C}) = \frac {e^{-1/2 (\mathbf{x}-\bar{z}(0) \mathbf{1})^\intercal (\sigma^2 \mathbf{C})^{-1} (\mathbf{x}-\bar{z}(0) \mathbf{1})}} {\sqrt{(2 \pi)^n det(\sigma^2 \mathbf{C})}} \label{4.5} \]
Aquí, los parámetros de nuestro modelo son σ 2 y\(\bar{z}(0)\), el valor de rasgo raíz. x es un vector n × 1 de valores de rasgo para la especie n punta en el árbol, con especies en el mismo orden que C, y 1 es un vector de columna n × 1 de unos. Obsérvese que (σ 2 C) −1 es la matriz inversa de la matriz σ 2 C
Como ejemplo, con los datos de mamíferos, podemos calcular la probabilidad para un modelo con valores de parámetros σ 2 = 1 y\(\bar{z}(0) = 0\). Necesitamos trabajar con ln-likelihoods (LnL), tanto porque el valor aquí es tan pequeño como para facilitar cálculos futuros, así:
\[lnL(\mathbf{x} | \bar{z}(0), \sigma^2, \mathbf{C}) = -116.2.\]
Para encontrar las estimaciones ML de los parámetros de nuestro modelo, necesitamos encontrar los valores de los parámetros que maximicen esa función. Una forma (no muy eficiente) de hacer esto es calcular la probabilidad a través de una amplia gama de valores de parámetros. Luego se puede visualizar la superficie de probabilidad resultante e identificar el máximo de la función de verosimilitud. Por ejemplo, la superficie de probabilidad para los datos del tamaño corporal del mamífero dado un modelo de movimiento browniano se muestra en la Figura 4.3. Tenga en cuenta que esta superficie tiene un pico alrededor de σ 2 = 0.09 y\(\bar{z}(0) = 4\). Inspeccionando la matriz de valores ML, encontramos la mayor probabilidad de lin (-78.05) a σ 2 = 0.089 y\(\bar{z}(0) = 4.65\).
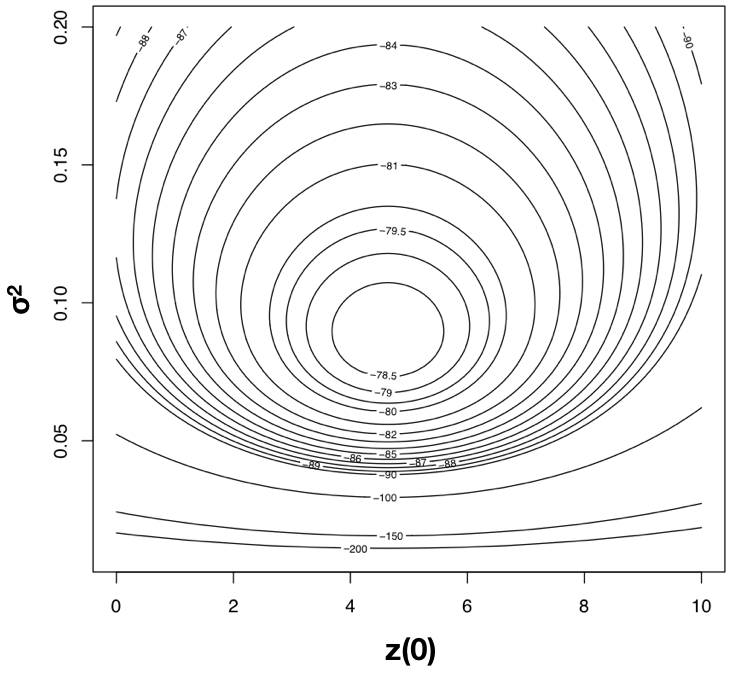
El cálculo descrito anteriormente es ineficiente, porque tenemos que calcular probabilidades en un amplio rango de valores de parámetros que están lejos de ser óptimos. Una mejor estrategia implica el uso de algoritmos de optimización, un campo de análisis matemático bien desarrollado (Nocedal y Wright 2006). Estos algoritmos difieren en sus detalles, pero podemos ilustrar cómo funcionan con un ejemplo general. Imagina que estás cerca de Mt. Santa Helens, y tienes la tarea de encontrar la cima de esa montaña. Está brumoso, pero puedes ver el área alrededor de tus pies y tener un altímetro preciso. Una estrategia es simplemente mirar la ladera de la montaña donde estás parado, y escalar cuesta arriba. Si la pendiente es empinada, probablemente todavía estés lejos de la cima, y deberías subir rápido; si la pendiente es poco profunda, podrías estar cerca de la cima de la montaña. Puede parecer obvio que esto te llevará a un pico local, pero quizás no al pico más alto del monte. Santa Helens. Los esquemas de optimización matemática también tienen esta dificultad potencial, pero usa algunos trucos para saltar en el espacio de parámetros e intentar encontrar el pico más alto general a medida que suben. Los detalles de los algoritmos de optimización reales están más allá del alcance de este libro; para más información, ver Nocedal y Wright (2006).
Un ejemplo sencillo se basa en el método de optimización de Newton [implementado, por ejemplo, por la función r nlm ()]. Podemos utilizar este algoritmo para encontrar rápidamente estimaciones de ML precisas 2.
Usando algoritmos de optimización encontramos una solución ML en\(\hat{\sigma}_{ML}^2 = 0.08804487\) y\(\hat{\bar{z}}(0) = 4.640571\), con l n L = −78.04942. Es importante destacar que la solución se puede encontrar con solo 10 cálculos de verosimilitud; este es el valor de buenos algoritmos de optimización. He trazado la ruta a través del espacio de parámetros tomada por el método de Newton al buscar el óptimo en la Figura 4.4. Observe dos cosas: primero, que la función comienza en algún momento y se dirige cuesta arriba sobre la superficie de verosimilitud hasta encontrar un óptimo; y segundo, que este cálculo requiere muchos menos pasos (y mucho menos tiempo) que calcular la probabilidad para un amplio rango de valores de parámetros.
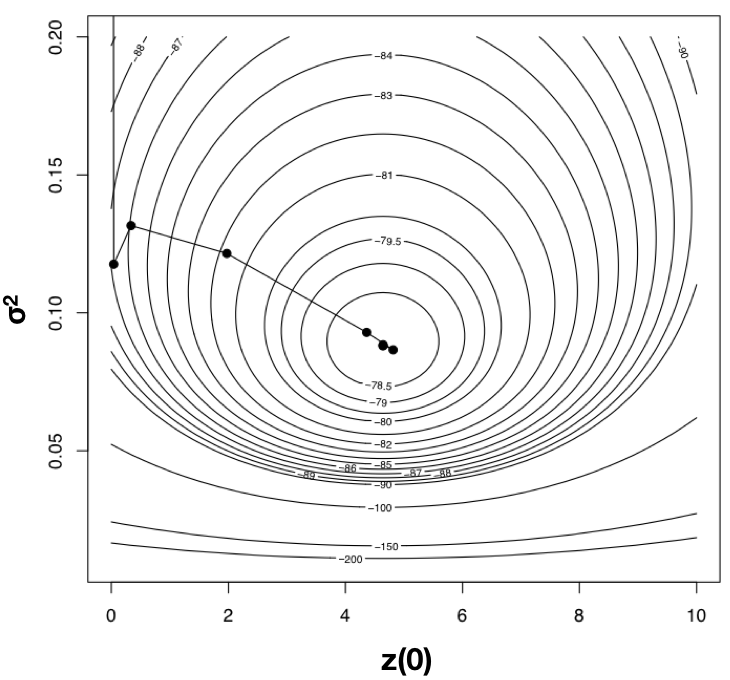
El uso de un algoritmo de optimización también tiene el beneficio agregado de proporcionar intervalos de confianza (aproximados) para valores de parámetros basados en el hessian de la superficie de verosimilitud. Este enfoque supone que la forma de la superficie de verosimilitud en las inmediaciones del pico puede aproximarse mediante una función cuadrática, y utiliza la curvatura de esa función, determinada por el hessian, para aproximar los errores estándar de los valores de los parámetros (Burnham y Anderson 2003). Si la superficie tiene un pico fuerte, los SE serán pequeños, mientras que si la superficie es muy ancha, los SE serán grandes. Por ejemplo, la superficie de probabilidad alrededor de los valores de ML para la evolución del tamaño corporal de los mamíferos tiene un hessian de:
\[ H = \begin{bmatrix} -314.6 & -0.0026\\ -0.0026 & -0.99 \\ \end{bmatrix} \label{4.6}\]
Esto da errores estándar de 0.13 (para $\ hat {\ sigma} _ {ML} ^2$) y 0.72 [para $\ hat {\ bar {\ bar {z}} (0) $]. Si asumimos que el error alrededor de estas estimaciones es aproximadamente normal, podemos crear estimaciones de confianza sumando y restando el doble del error estándar. Luego obtenemos IC 95% de 0.06 − 0.11 (para\(\hat{\sigma}_{ML}^2\)) y 3.22 − 6.06 [para\(\hat{\bar{z}}(0)\)].
El peligro en los algoritmos de optimización es que a veces uno puede quedar atascado en picos locales. Algoritmos más elaborados repetidos para múltiples puntos de partida pueden ayudar a resolver este problema, pero no son necesarios para el simple movimiento browniano en un árbol como se considera aquí. La optimización numérica es un problema difícil en los métodos comparativos filogenéticos, especialmente para los desarrolladores de software.
En el caso particular de ajustar el movimiento browniano a los árboles, resulta que incluso nuestro algoritmo rápido para la optimización era innecesario. En este caso, la estimación de máxima verosimilitud para cada uno de estos dos parámetros puede calcularse analíticamente (O'Meara et al. 2006).
\[ \hat{\bar{z}}(0) = (\mathbf{1}^\intercal \mathbf{C}^{-1} \mathbf{1})^{-1} (\mathbf{1}^\intercal \mathbf{C}^{-1} \mathbf{x}) \label{4.7}\]
y:
\[ \hat{\sigma}_{ML}^2 = \frac {(\mathbf{x} - \hat{\bar{z}}(0) \mathbf{1})^\intercal \mathbf{C}^{-1} (\mathbf{x} - \hat{\bar{z}}(0) \mathbf{1})} {n} \label{4.8}\]
donde n es el número de taxones en el árbol, C es la matriz de varianza-covarianza n × n bajo movimiento browniano para caracteres de punta dado el árbol filogenético, x es un vector n × 1 de valores de rasgos para especies de punta en el árbol, 1 es un vector de columna n × 1 de unos, $\ hat {\ bar {z}} (0) $ es el estado raíz estimado para el carácter, y $\ hat {\ sigma} _ {ML} ^2$ es la tasa neta estimada de evolución.
Aplicando este enfoque al tamaño corporal de los mamíferos, obtenemos estimaciones que son exactamente las mismas que nuestros resultados a partir de la optimización numérica: $\ hat {\ sigma} _ {ML} ^2 = 0.088$ y\(\hat{\bar{z}}(0) = 4.64\).
La ecuación (4.8) es sesgada, y estimará consistentemente tasas de evolución que son un poco demasiado pequeñas; una versión imparcial basada en verosimilitud máxima restringida (REML) y utilizada por Garland (1992) y otros es:
\[ \hat{\sigma}_{REML}^2 = \frac {(\mathbf{x} - \hat{\bar{z}}(0) \mathbf{1})^\intercal \mathbf{C}^{-1} (\mathbf{x} - \hat{\bar{z}}(0) \mathbf{1})}{n-1} \label{4.9}\]
Esta corrección cambia nuestra estimación de la tasa de tamaño corporal en mamíferos de\(\hat{\sigma}_{ML}^2 = 0.088\) a\(\hat{\sigma}_{REML}^2 = 0.090\). La ecuación\ ref {4.8} es exactamente idéntica a la tasa estimada de evolución calculada utilizando el contraste independiente al cuadrado promedio, descrito anteriormente; es decir,\(\hat{\sigma}_{PIC}^2 = \hat{\sigma}_{REML}^2\). De hecho, los PIC son una formulación de un modelo REML. La parte “restringida” de REML se refiere al hecho de que estos métodos calculan probabilidades a partir de un conjunto transformado de datos donde se ha eliminado el efecto de parámetros molestos. En este caso, el parámetro de molestia es el estado raíz estimado\(\hat{\bar{z}}(0)\) 3.
Para el ejemplo del tamaño corporal del mamífero, podemos explorar más a fondo la diferencia entre REML y ML en términos de intervalos de confianza estadísticos usando probabilidades basadas en los contrastes. Suponemos, nuevamente, que todos los contrastes se extraen de una distribución normal con media 0 y varianza desconocida. Si nuevamente usamos el método de Newton para la optimización, encontramos una probabilidad logarítmica máxima de -10.3 en\(\hat{\sigma}_{REML}^2 = 0.090\). Esto devuelve una matriz de 1 × 1 para el hessian con un valor de 2957.8, correspondiente a una SE de 0.018. Esta SE ligeramente mayor corresponde a IC 95% para\(\hat{\sigma}_{REML}^2\) de 0.05 − 0.13.
En el contexto de los métodos comparativos, REML tiene dos ventajas principales. Primero, los PICs tratan el estado raíz del árbol como un parámetro de molestia. Normalmente tenemos muy poca información sobre este estado raíz, por lo que eso puede ser una ventaja del enfoque REML. Segundo, los PIC son fáciles de calcular para árboles filogenéticos muy grandes porque no requieren la construcción (¡o inversión!) de cualquier matriz de varianza-covarianza grande. Esto es importante para los grandes árboles filogenéticos. Imagínese que teníamos un árbol filogenético de todos los vertebrados (~60,000 especies) y queríamos calcular la tasa de evolución del tamaño corporal. Para utilizar la máxima verosimilitud estándar, tenemos que calcular C, una matriz con 60, 000 × 60, 000 = 3.6 mil millones de entradas, e invertirla para calcular C −1. Para calcular los PIC, por el contrario, sólo tenemos que realizar del orden de 120,000 operaciones. Agradecidamente, ahora hay algoritmos de poda para calcular rápidamente las probabilidades de árboles grandes bajo una variedad de modelos diferentes (ver, por ejemplo, FitzJohn 2012; Freckleton 2012; y Ho y Ané 2014).


