8.6: Prueba de diferencias en la tasa de cambio de carácter hacia adelante y hacia atrás

A lo largo de este capítulo me he estado refiriendo a un ejemplo de evolución de miembros lagartos, pero aún no hemos probado la hipótesis que señalé en la introducción: que las tasas de transición para perder extremidades son mayores que las tasas de ganancia de extremidades.

Para ello, podemos comparar nuestro modelo Mk de una tasa con un modelo de dos velocidades con diferencias en la tasa de transiciones hacia adelante y hacia atrás. Los estados de carácter son 1 (sin extremidades) y 2 (extremidades), y la transición hacia adelante representa extremidades ganadoras. Se trata de un caso especial del modelo de “todas las tasas diferentes” que se discute en el capítulo dos. Las matrices Q para estos dos modelos serán, para el modelo 1 (tasas iguales):

\[ \mathbf{Q_{ER}} = \begin{bmatrix} -q & q \\ q & -q \\ \end{bmatrix} \label{8.3A} \]

\[ \mathbf{\pi_{ER}} = \begin{bmatrix} 1/2 & 1/2 \\ \end{bmatrix} \label{8.3B}\]

Y para el modelo 2, asimétrico:

\[ \mathbf{Q_{ASY}} = \begin{bmatrix} -q_1 & q_1 \\ q_2 & -q_2 \\ \end{bmatrix} \label{8.4A} \]

\[ \mathbf{\pi_{ASY}} = \begin{bmatrix} 1/2 & 1/2 \\ \end{bmatrix} \label{8.4B} \]

Observe que el modelo ER tiene un parámetro, mientras que el modelo ASY tiene dos. También hemos especificado probabilidades iguales de cada carácter en la raíz del árbol, lo que puede no estar justificado. Pero esta comparación sigue siendo útil como ejemplo sencillo.

Se pueden comparar los dos modelos anidados utilizando métodos estándar discutidos en capítulos anteriores, es decir, una prueba de relación de probabilidad, AIC, BIC u otros métodos similares.

Podemos aplicar todos los métodos anteriores para analizar la evolución de la limosidad en los escuamates. Podemos utilizar los datos de árbol y estado de carácter de Brandley et al. (2008), que se traza con reconstrucciones de estado ancestrales bajo un modelo ER en la Figura 8.2.

Figura 8.2. Patrones reconstruidos de la evolución de las extremidades y la falta de limaza a través de los escamados Los consejos muestran estados de taxones existentes (aquí, clasifiqué especies sin extremidades delanteras ni posteriores como sin extremidades inferiores, lo cual es conservador dada la variación a lo largo de este clado (ver capítulo 7). Los gráficos circulares en los nodos internos muestran probabilidades marginales proporcionales para la reconstrucción del estado ancestral bajo un modelo de ER. Datos de Brandley et al. (2008). Imagen del autor, puede ser reutilizada bajo licencia CC-BY-4.0.

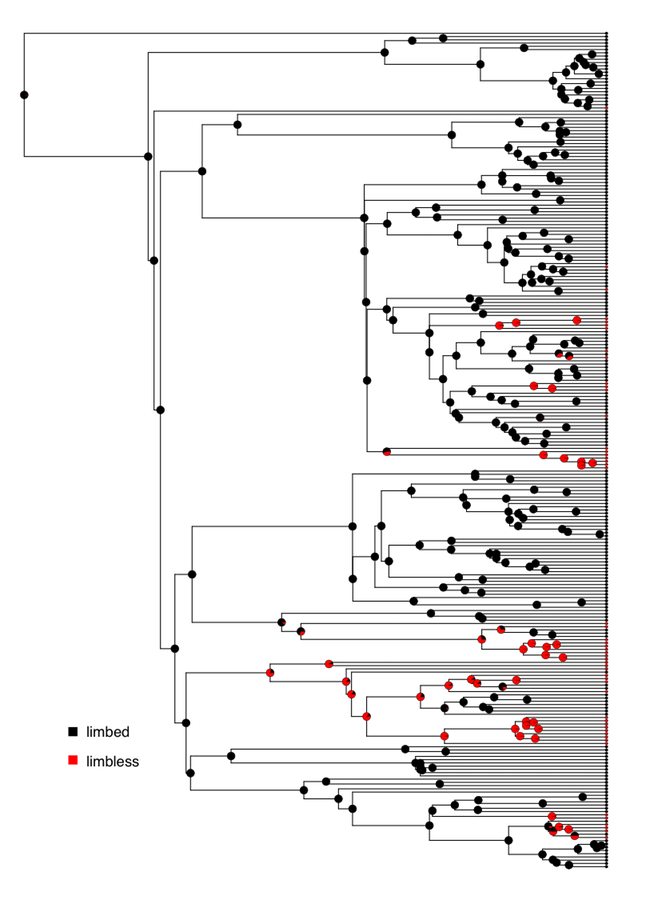
Si ajustamos un modelo Mk a estos datos asumiendo frecuencias de estado iguales en la raíz del árbol, obtenemos una LnL de -80.5 y una estimación de la matriz Q _E R como:

\[ \mathbf{Q_{ER}} = \begin{bmatrix} -0.0019 & 0.0019 \\ 0.0019 & -0.0019 \\ \end{bmatrix} \label{8.5}\]

El modelo ASY con diferentes tasas hacia adelante y hacia atrás da una LnL de -79.4 y:

\[ \mathbf{Q_{ASY}} = \begin{bmatrix} -0.0016 & 0.0016 \\ 0.0038 & -0.0038 \\ \end{bmatrix} \label{8.6} \]

Obsérvese que el modelo ASY tiene una tasa más alta hacia atrás que hacia adelante; como se esperaba, estimamos una tasa de pérdida de extremidades que es mayor que la tasa de ganarlas (aunque la diferencia es sorprendentemente baja). ¿Esto se apoya estadísticamente? Podemos comparar las puntuaciones AIC de los dos modelos. Para el modelo ER, A I C _c = 163.0, mientras que para el modelo ASY A I C _c = 162.8. El puntaje de AICc es mayor para el modelo de tasas desiguales, pero solo en aproximadamente 0.2, lo que no es definitivo de ninguna manera. Entonces, con base en este análisis, no podemos descartar la posibilidad de que las tasas hacia adelante y hacia atrás sean iguales.

Un análisis bayesiano del modelo ASY da conclusiones similares (Figura 8.3). Podemos ver que la distribución posterior para la tasa hacia atrás (q ₂₁) es mayor que la tasa de avance (q ₁₂), pero que las dos distribuciones se superponen ampliamente.

Figura 8.3. Distibuciones posteriores bayesianas para el modelo extendido-MK aplicadas a la evolución de la limosidad en los escuamates. Imagen del autor, puede ser reutilizada bajo licencia CC-BY-4.0.

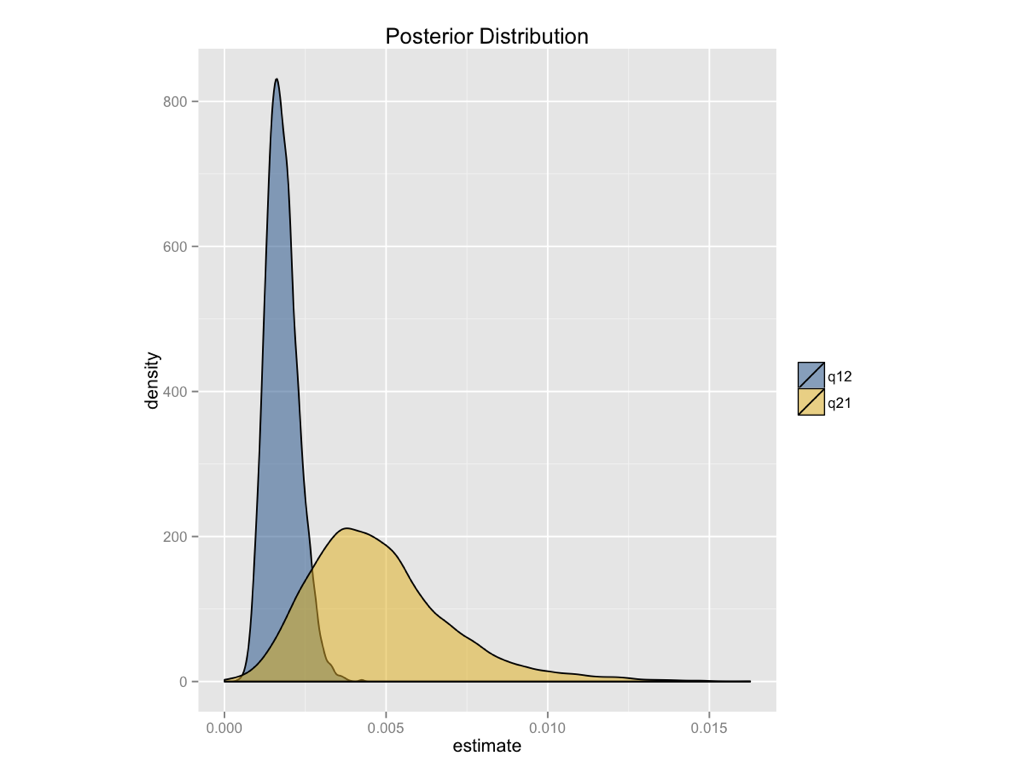
Quizás te preguntes cómo podemos conciliar estos resultados, que sugieren que los escamados ganan extremidades al menos con la misma frecuencia que las pierden, con nuestra intuición biológica de que las extremidades deberían ser mucho más difíciles de ganar que perder. Pero tenga en cuenta que nuestro análisis comparativo no está utilizando ninguna información que no sea los estados de las especies existentes para reconstruir estas tasas. En particular, identificar la evolución irreversible utilizando métodos comparativos es un problema que se sabe que es bastante difícil, y podría requerir información externa para resolverlo de manera concluyente. Por ejemplo, si tuviéramos alguna información sobre el número relativo de pasos mutacionales requeridos para ganar y perder extremidades, podríamos usar un previo informativo —que, sospecho, sugeriría que las extremidades son más difíciles de ganar que de perder. Tal previo podría alterar drásticamente los resultados presentados en la Figura 8.3. Volveremos al problema de la evolución irreversible más adelante en el libro (Capítulo 13).