9.5: Modelos de Umbral

Recientemente, Joe Felsenstein (2005, 2012) introdujo un modelo desde la genética cuantitativa, el modelo umbral, hasta métodos comparativos. Los modelos de umbral funcionan modelando un carácter discreto como sustentado por algún otro rasgo continuo, no observado (llamado pasivo). Si el pasivo cruza un cierto valor umbral, entonces el estado discreto cambia. Más específicamente, podemos considerar un solo rasgo, y, con dos estados, 0 y 1, que a su vez está determinado por alguna variable continua subyacente, x, llamada el pasivo. Si x es mayor que el umbral, t, entonces y es 1; de lo contrario, y es 0. Felsenstein (2005) asume que x evoluciona bajo un modelo de movimiento browniano, aunque otros modelos como OU son, en principio, posibles.

Podemos encontrar la probabilidad de este modelo considerando las observaciones de estados de carácter en las puntas del árbol. Observamos el estado de cada especie, y _i. Desconocemos los valores de responsabilidad para estas especies. Sin embargo, tratamos estos pasivos como no observados y consideramos sus distribuciones. Bajo un modelo de movimiento browniano, sabemos que los pasivos seguirán una distribución normal multivariada (ver capítulo 3). Podemos calcular la probabilidad de observar los datos (y _i) encontrando la integral de las distribuciones de pasivos en el lado del umbral que coincide con los datos. Entonces, si la distribución del pasivo por la especie i es p _i (x), entonces:

\[ p(y_i = 0) = {\int\limits_{-\infty}^{t} p_i (x) dx} \label{9.1}\]

y

\[ p(y_i = 1) = {\int\limits_{t}^{\infty} p_i (x) dx} \]

(ver Figura 9.3 para una ilustración de este cálculo, que es más fácil de lo que parece ya que existen fórmulas estándar para encontrar el área bajo una distribución normal).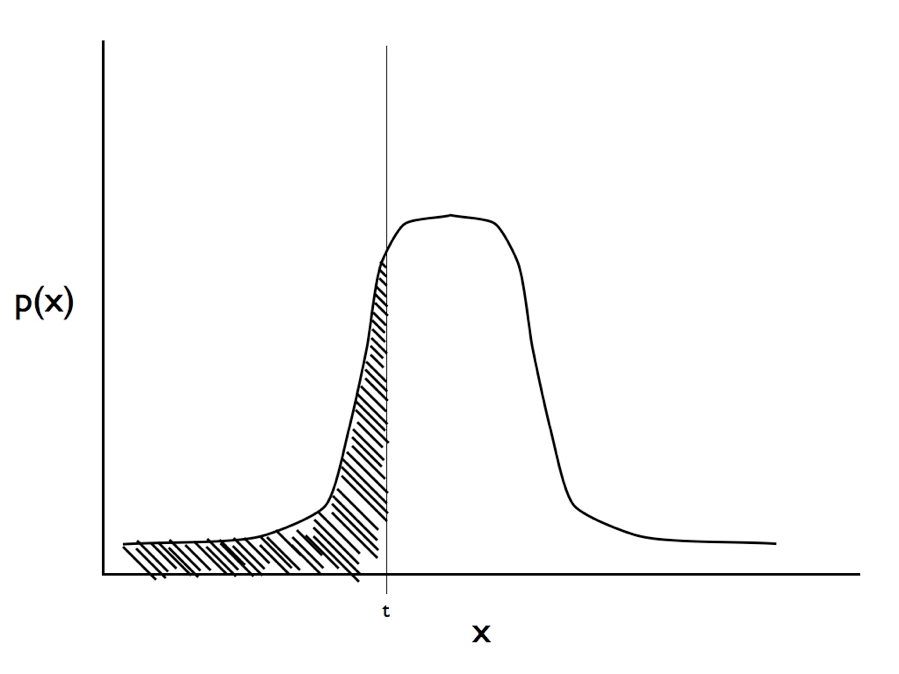

Figura 9.3. Ilustración de la integral en la Ecuación\ ref {9.1}. Para un rasgo con estado cero observado calculamos el área bajo la curva desde infinito negativo hasta el umbral t. La imagen del autor, puede ser reutilizada bajo licencia CC-BY-4.0.

Se puede ajustar este modelo usando métodos estándar ML o bayesianos. Las implementaciones actuales incluyen un algoritmo de maximización de expectativas (EM) (Felsenstein 2005, 2012) y un MCMC bayesiano (Revell 2014).

El modelo de umbral difiere en algunas formas clave de los modelos estándar tipo MK. En primer lugar, los caracteres umbral evolucionan de manera diferente a los caracteres que no son umbrales debido a su responsabilidad subyacente. En particular, la tasa efectiva de cambio del carácter discreto depende de la cantidad de tiempo que un linaje haya estado en ese estado de carácter. Es probable que los caracteres que acaban de cambiar (digamos, de 0 a 1) vuelvan a cambiar (de 1 a 0), ya que es probable que el pasivo esté cerca del umbral. Por el contrario, los personajes que han estado en un estado u otro durante mucho tiempo tienden a ser más improbables de cambiar (ya que la responsabilidad probablemente esté muy lejos del umbral). Esta diferencia coincide con la intuición biológica para algunos personajes, donde millones de años en un estado significa que el cambio a un estado diferente podría ser poco probable. Este comportamiento del modelo de umbral puede explicar potencialmente la variación en las tasas de transición entre clados sin agregar parámetros adicionales del modelo. Segundo, el modelo de umbral escala para cubrir más de un carácter más fácilmente que los modelos Mk. Finalmente, en un marco de umbral, es sencillo extender el modelo para incluir una mezcla de caracteres tanto discretos como continuos; básicamente, se asume que los caracteres continuos son como “pasivos observados”, y pueden modelarse junto con los caracteres discretos.