9.7: Pruebas para la evolución no independiente de diferentes personajes
- Page ID
- 54034
Las hipótesis en biología evolutiva a menudo se relacionan con si dos (o más) rasgos afectan la evolución entre sí (Capítulo 5). Uno puede tener una correlación estándar entre dos rasgos discretos si conocer el estado de un rasgo le permite predecir el estado del otro. Sin embargo, en la evolución, estas correlaciones surgirán debido a los patrones compartidos de relación entre especies. Normalmente nos interesan más las correlaciones evolutivas (Capítulo 5). Con rasgos discretos, podemos definir correlaciones evolutivas de una manera específica: dos rasgos discretos comparten una correlación evolutiva si el estado de un personaje afecta las tasas de transición relativas de un segundo.
Imagínese que estamos considerando la evolución de dos rasgos, rasgo 1 y rasgo 2, en un árbol filogenético. Ambos rasgos tienen dos posibles estados de carácter, uno y cero. Podemos mostrar estos dos rasgos visualmente como Figura 9.4.
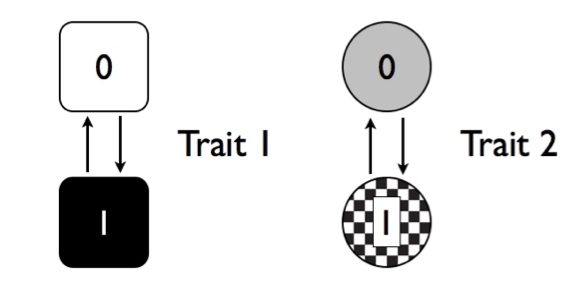
En la figura, cada rasgo tiene dos posibles tasas de transición, de 0 a 1 y de 1 a 0. Por ahora, supongamos que las tasas hacia atrás y hacia adelante son iguales. Cualquier especie puede tener una de las cuatro combinaciones posibles de los dos rasgos (00, 01, 10 u 11). Podemos dibujar las transiciones entre estas cuatro combinaciones como Figura 9.5.
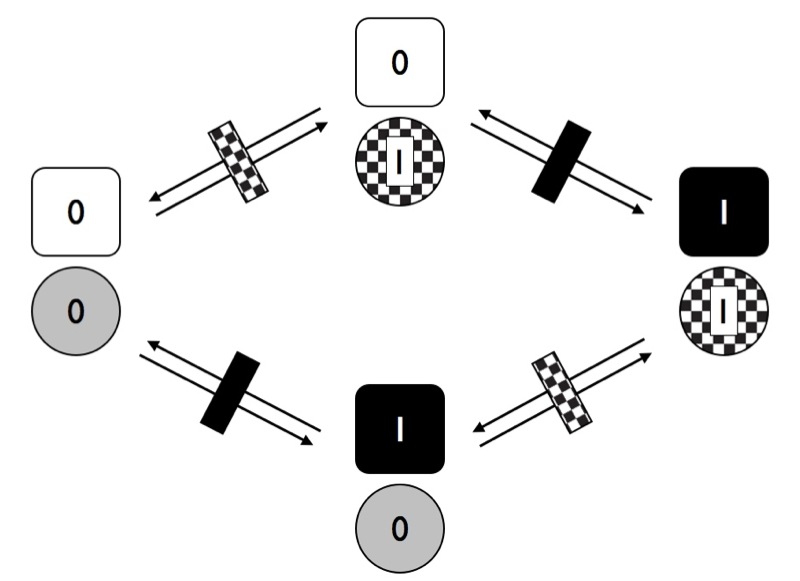
Figura 9.5. Transiciones entre estados para dos rasgos con dos estados de carácter cada uno donde los personajes evolucionan independientemente uno del otro. Imagen del autor, puede ser reutilizada bajo licencia CC-BY-4.0.
En la Figura 9.6, he marcado las distintas tasas con diferentes rectángulos: el negro representa los cambios en el rasgo 1, mientras que los cuadros son los cambios en el rasgo 2. Observe que, en esta figura, estamos asumiendo que los dos rasgos son independientes. Es decir, en este modelo las tasas de transición del rasgo uno no dependen del estado del rasgo 2, y viceversa. ¿Qué pasaría con nuestro modelo si permitimos que los rasgos evolucionen de manera dependiente?
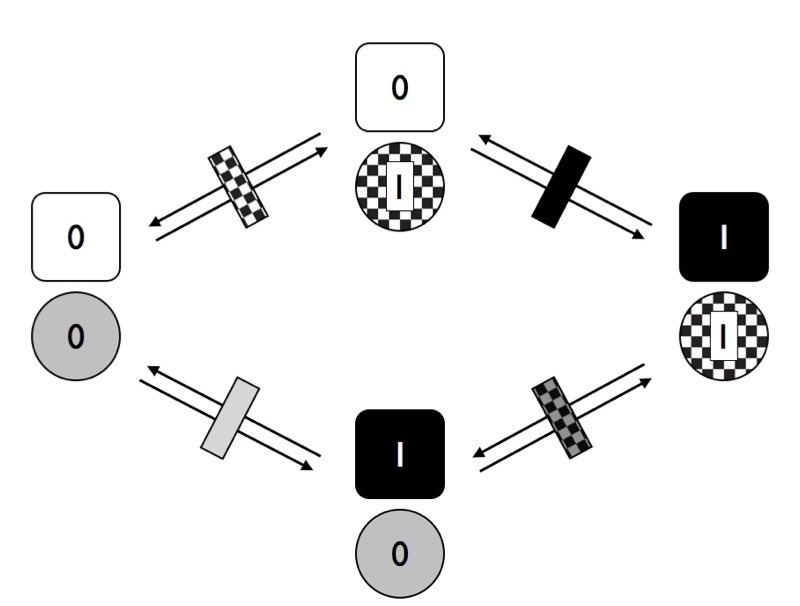
Figura 9.6. Transiciones entre estados para dos rasgos con dos estados de carácter cada uno donde los personajes evolucionan a ritmos que dependen del estado de carácter del otro rasgo. Imagen del autor, puede ser reutilizada bajo licencia CC-BY-4.0.
Observe que en la Figura 9.6, tenemos cuatro tasas de transición diferentes. Considera primero los rectángulos sólidos. El rectángulo gris representa la tasa de transición para el rasgo 1 cuando el rasgo 2 tiene el estado 0, mientras que el rectángulo negro representa la tasa de transición para el rasgo 1 cuando el rasgo 2 tiene el estado 1. Si estas dos tasas son diferentes, entonces los rasgos dependen entre sí, es decir, la tasa de evolución del rasgo 1 depende del estado de carácter del rasgo 2.
Estos dos modelos tienen diferentes números de parámetros, pero son relativamente fáciles de ajustar utilizando el enfoque de máxima verosimilitud descrito en este capítulo. La clave es anotar la matriz de transición (Q) para cada modelo. Por ejemplo, una matriz de transición para el modelo en la figura 9.4 es:
\[ \mathbf{Q} = \begin{bmatrix} -q_1 - q_2 & q_1 & q_2 & 0\\ q_1 & -q_1 - q_2 & 0 & q_2\\ q_2 & 0 & -q_1 - q_2 & q_1\\ 0 & q_2 & q_1 & -q_1 - q_2\\ \end{bmatrix} \label{9.2}\]
En la matriz anterior, cada fila y columna corresponde a una combinación particular de estados para los caracteres 1 y 2: (0,0), (0,1), (1,0) y (1,1). Tenga en cuenta que algunas posibles transiciones en este modelo tienen tasa 0, lo que significa que no ocurren. Estas son transiciones que requerirían que ambos caracteres cambiaran exactamente simultáneamente (por ejemplo, (0,0) a (1,1), una posibilidad que se excluye de este modelo.
Del mismo modo, podemos escribir una matriz de transición para el modelo en la figura 9.5:
\[ \mathbf{Q} = \begin{bmatrix} -q_1 - q_2 & q_1 & q_2 & 0\\ q_1 & -q_1 - q_3 & 0 & q_3\\ q_2 & 0 & -q_2 - q_4 & q_4\\ 0 & q_3 & q_4 & -q_3 - q_4\\ \end{bmatrix} \label{9.3}\]
Observe que el modelo de evolución simple e independiente de 2 parámetros es un caso especial del modelo dependiente de 4 parámetros más complejo. Debido a esto, podemos comparar los dos con una prueba de razón de verosimilitud. Alternativamente, se pueden usar factores AIC o Bayes. Si encontramos soporte para el modelo de 4 parámetros, podemos concluir que la evolución de al menos uno de los dos caracteres depende del estado del otro.
Vale la pena señalar que existen otros modelos que uno puede caber para la evolución de dos rasgos binarios que no comenté anteriormente. Por ejemplo, se puede modelar la situación en la que cada uno de los dos rasgos tiene diferentes tasas hacia adelante y hacia atrás, pero están evolucionando de manera independiente. Se trata de un modelo de cuatro parámetros. Adicionalmente, uno puede permitir que tanto las tasas hacia adelante como hacia atrás difieran y dependan del estado de carácter del otro rasgo: un modelo de ocho parámetros. Este es el modelo que uno necesita para ver verdaderamente una correlación entre los dos caracteres, uno donde ciertas combinaciones tienden a acumularse en el árbol. Todos estos modelos, y otros que no se describen aquí, se pueden comparar usando factores AIC, BIC o Bayes. Pagel y Meade (2006) describen un método particularmente innovador y sintético para probar hipótesis sobre la evolución correlacionada de caracteres discretos en un marco bayesiano usando MCMC de salto reversible.
También se pueden probar correlaciones entre caracteres discretos usando modelos de umbral. Aquí, se prueba si los pasivos de los dos personajes evolucionan o no de manera correlacionada. Más específicamente, podemos modelar pasivos para los dos caracteres de umbral utilizando un modelo de movimiento browniano bivariado, con alguna covarianza evolutiva σ 12 2 entre los dos pasivos. Entonces podemos usar métodos ML o Bayesianos para determinar si la covarianza evolutiva entre los dos caracteres es distinta de cero (siguiendo los métodos descritos en el capítulo 5, pero usando probabilidades basadas en caracteres discretos como se describió anteriormente).

