10.5: Topología de árboles, forma de árbol y equilibrio de árboles bajo un modelo de nacimiento-muerte
- Page ID
- 53873
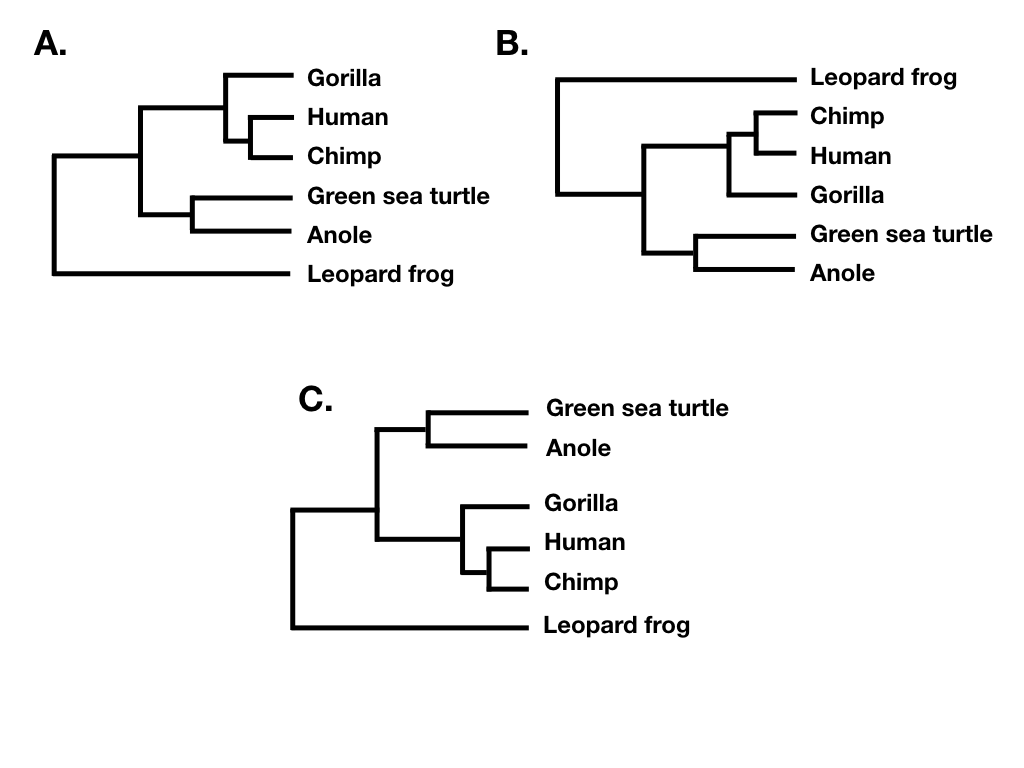
La topología de árboles resume los patrones de relación evolutiva entre un grupo de especies independientemente de las longitudes de rama de un árbol filogenético. Dos árboles diferentes tienen la misma topología si definen exactamente el mismo conjunto de clados. Esto es importante porque a veces dos árboles pueden verse muy diferentes y aún así tener la misma topología (por ejemplo, Figura 10.6 A, B y C).
La forma del árbol ignora tanto la longitud de las ramas como las etiquetas de las puntas Por ejemplo, los dos árboles de la figura 10.7 A y B tienen la misma forma de árbol a pesar de que no comparten puntas en común. Lo que sí comparten es que sus nodos tienen los mismos patrones en cuanto al número de descendientes en cada “lado” de la bifurcación. Por el contrario, el árbol filogenético en 10.7 C tiene una forma diferente. (Tenga en cuenta que lo que estoy llamando forma de árbol a veces se conoce como topología de árbol “sin etiquetar”; por ejemplo, Felsenstein 2004).
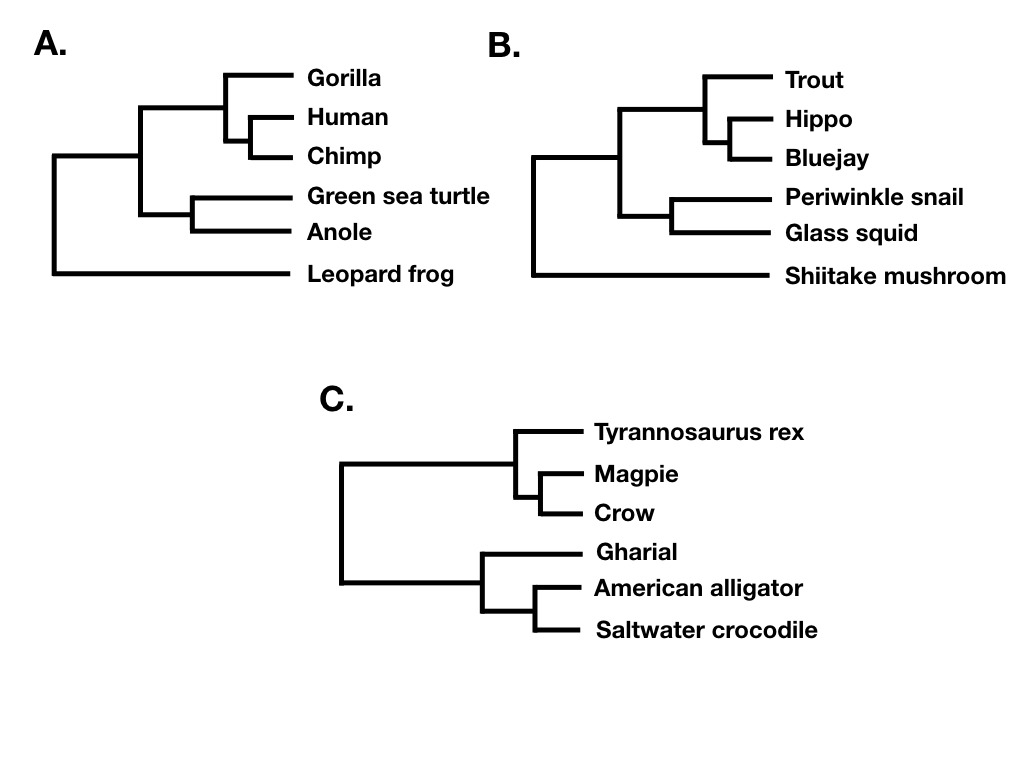
Finalmente, el equilibrio de árboles es una forma de expresar diferencias en el número de descendientes entre pares de linajes hermanos en diferentes puntos de un árbol filogenético. Por ejemplo, consideremos el árbol filogenético representado en la figura 10.7B. La división más profunda de ese árbol separa un clado con cinco especies (trucha, hipopótamo, azulado, caracol bígaro, calamar de cristal) de un clado con una sola especie (hongo Shiitake), y así ese nodo en el árbol está desequilibrado con un patrón (5, 1). Por el contrario, la división más profunda en 10.7C separa dos clados de igual tamaño. En ese árbol, el nodo más profundo se equilibra con un patrón (3, 3). Una serie de enfoques en macroevolución utilizan el equilibrio en los nodos y en árboles enteros para tratar de capturar patrones evolutivos importantes.
Podemos comenzar a entender estos enfoques considerando el equilibrio de un solo nodo n en un árbol filogenético. Hay dos clados que descienden de este nodo; llamémoslos a y b. Suponemos que el número total de especies descendidas del nodo N t o t a l = N a + N b es constante y que ni N a ni N b es cero. Un resultado importante, discutido por primera vez por Farris (1976) para un modelo de nacimiento puro, es que todas las divisiones numéricas posibles de N t o t a l en N a + N b son igualmente probables. Por ejemplo, si N t o t a l = 10, entonces todas las divisiones posibles: 1 + 9, 2 + 8, 3 + 7, 4 + 6, 5 + 5, 6 + 4, 7 + 3, 8 + 2 y 9 + 1 son todas igualmente probables, de manera que se predice que cada una ocurrirá con una probabilidad 1/9. Formalmente,
\[ p(N_a \mid N_{total})=\frac{1}{N_{total}-1} \label{19.17}\]
Obsérvese que existe una sutil diferencia entre la ecuación 10.2 anterior y algunas ecuaciones en la literatura, por ejemplo Slowinski y Guyer (1993). Esta diferencia tiene que ver con si etiquetamos los dos clados descendientes, a y b, o no; si los clados no están etiquetados, entonces no hay diferencia entre 4+6 y 6+4, de manera que la probabilidad de que el clado más grande, cualquiera que sea, tenga 6 especies es el doble de lo que da mi ecuación.
La Ecuación 10.17 se aplica aunque haya extinción, siempre y cuando ambos clados hermanos tengan las mismas tasas de especiación y extinción (Slowinski y Guyer 1993). Esta ecuación se ha utilizado para comparar las tasas de diversificación entre clados hermanos, ya sea para un solo par o a través de múltiples pares (ver Capítulo 11).
Las estadísticas de balance de árboles proporcionan una forma de comparar números de taxones en todos los nodos de un árbol filogenético simultáneamente. Hay un número sorprendentemente grande de estadísticas de balance de árboles, pero todas se basan en resumir información sobre el saldo de cada nodo a través de un árbol entero. El índice I c (Colless 1982) de Colless es uno de los índices más simples —y quizás más utilizados— del balance arbóreo. I c es la suma de la diferencia en el número de puntas subtendidas a cada lado de cada nodo del árbol, estandarizada por el máximo que tal suma puede lograr:
\[ I_C = \frac{\sum\limits_{all nodes} (N_L - N_R)}{(N-1)(N-2)/2} \label{10.18}\]
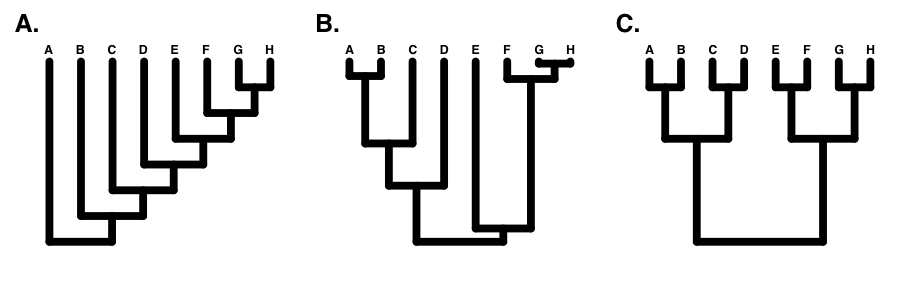
Si el árbol está perfectamente equilibrado (solo es posible cuando N es alguna potencia de 2, por ejemplo 2, 4, 8, 16, etc.), entonces I C = 0 (Figura 10.7C). Por el contrario, si el árbol es completamente pectinado, lo que significa que cada división en el árbol contrasta un clado con 1 especie con el resto de las especies en el clado, entonces I C = 1 (Figura 10.7A). Todos los árboles filogenéticos tienen valores de I C entre 0 y 1 (Figura 10.7B).
Existen otros índices de balance filogenético de árboles (revisados en Mooers y Heard 1997). Todos estos índices se utilizan de manera similar: entonces se puede comparar el valor del índice del árbol con lo que uno podría esperar bajo un modelo particular de diversificación, típicamente nacimiento-muerte. De hecho, dado que estos índices se centran en la topología del árbol e ignoran las longitudes de las ramas, en realidad se puede considerar su comportamiento general bajo un conjunto de modelos de Markov (ERM) de tasas iguales. Este conjunto incluye cualquier modelo donde las tasas de nacimiento y mortalidad sean iguales en todos los linajes de un árbol filogenético en un momento determinado. Los modelos ERM incluyen modelos de nacimiento-muerte como se describió anteriormente, pero también abarcan modelos donde las tasas de nacimiento y/o mortalidad cambian a través del tiempo.


