12.5: Especiación prolongada
- Page ID
- 54368
En todos los modelos de diversificación que hemos considerado hasta ahora, la especiación ocurre instantáneamente; en un momento tenemos una sola especie, y luego inmediatamente dos. Pero esto no es biológicamente plausible. La especiación lleva tiempo, como lo demuestra el creciente número de poblaciones parcialmente distintas que los biólogos han identificado en el mundo natural (Coyne y Orr 2004; De Queiroz 2005). Además, el hecho de que la especiación lleve tiempo puede tener un profundo impacto en las formas de los árboles filogenéticos (Losos y Adler 1995). Debido a esto, vale la pena considerar modelos de diversificación que expliquen explícitamente que el proceso de especiación tiene un principio y un fin.
Los modelos más exitosos para abordar esta cuestión han sido los modelos de especiación prolongada (Rosindell et al. 2010; Etienne y Rosindell 2012; Lambert et al. 2015). Una forma de establecer dicho modelo es afirmar que la especiación comienza por la formación de una especie incipiente a algún ritmo λ 1. Esto representa una especie “parcial”; se puede imaginar, por ejemplo, que se trata de una población que se ha separado del área de distribución principal de la especie, pero que aún no ha evolucionado el aislamiento reproductivo completo. La especie incipiente sólo se convierte en una especie “completa” si completa la especiación, la cual ocurre a una tasa λ 2. Esto representa la velocidad a la que una especie incipiente evoluciona el estado completo de especie (Figura 12.5).
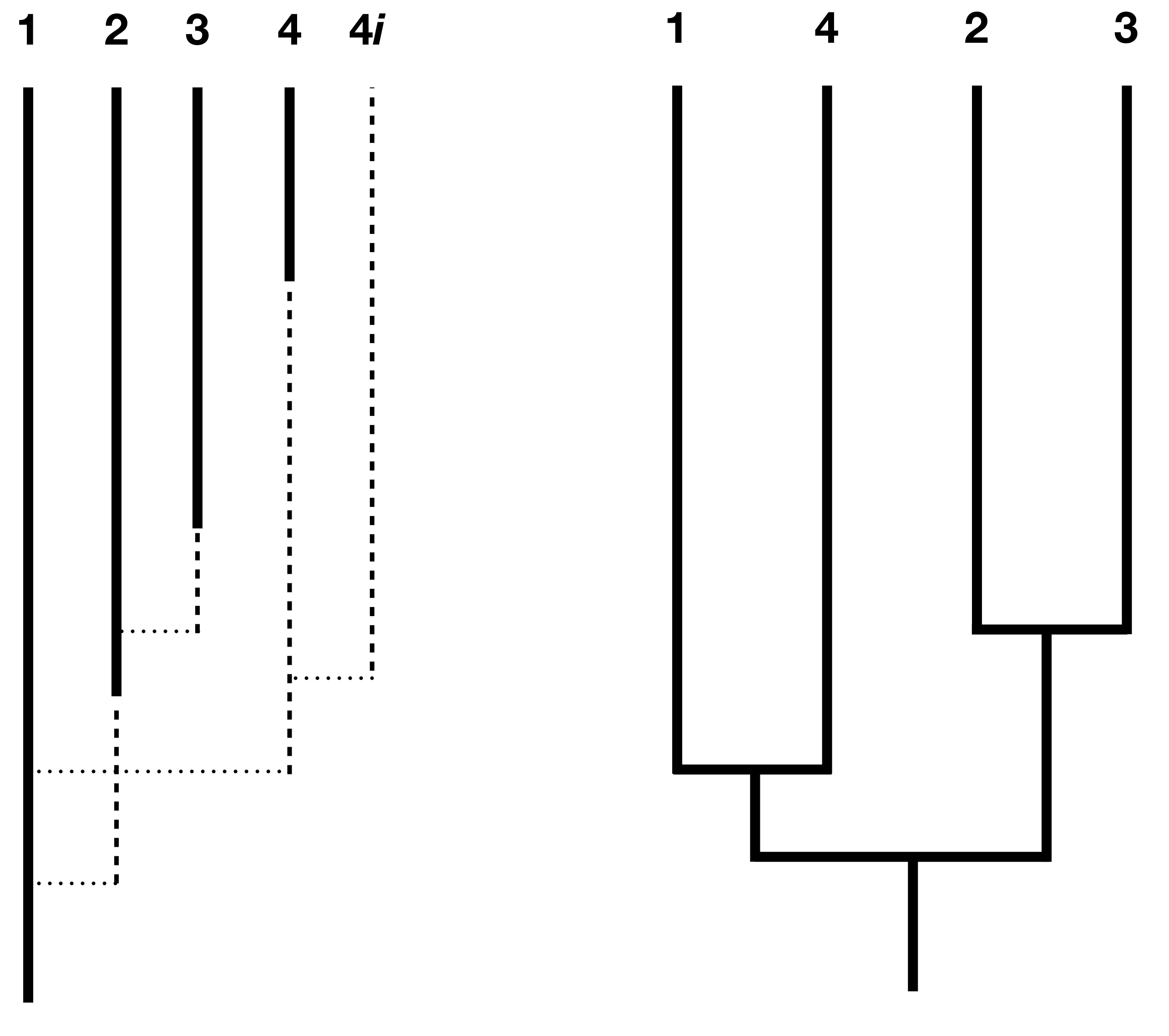
Debido a que la especiación lleva tiempo, el principal impacto de este modelo es que predecimos menos especies muy jóvenes en nuestro árbol, es decir, los nodos más cercanos a las puntas del árbol no son tan jóvenes como se compararían con los modelos de nacimiento puro o nacimiento-muerte sin especiación prolongada (Figura 12.6). Como resultado, los modelos de especiación prolongados producen linaje a través de parcelas de tiempo que pueden imitar las propiedades que a menudo se atribuyen a la dependencia de la diversidad, ¡incluso sin ninguna interacción entre linajes (Etienne y Rosindell 2012)!
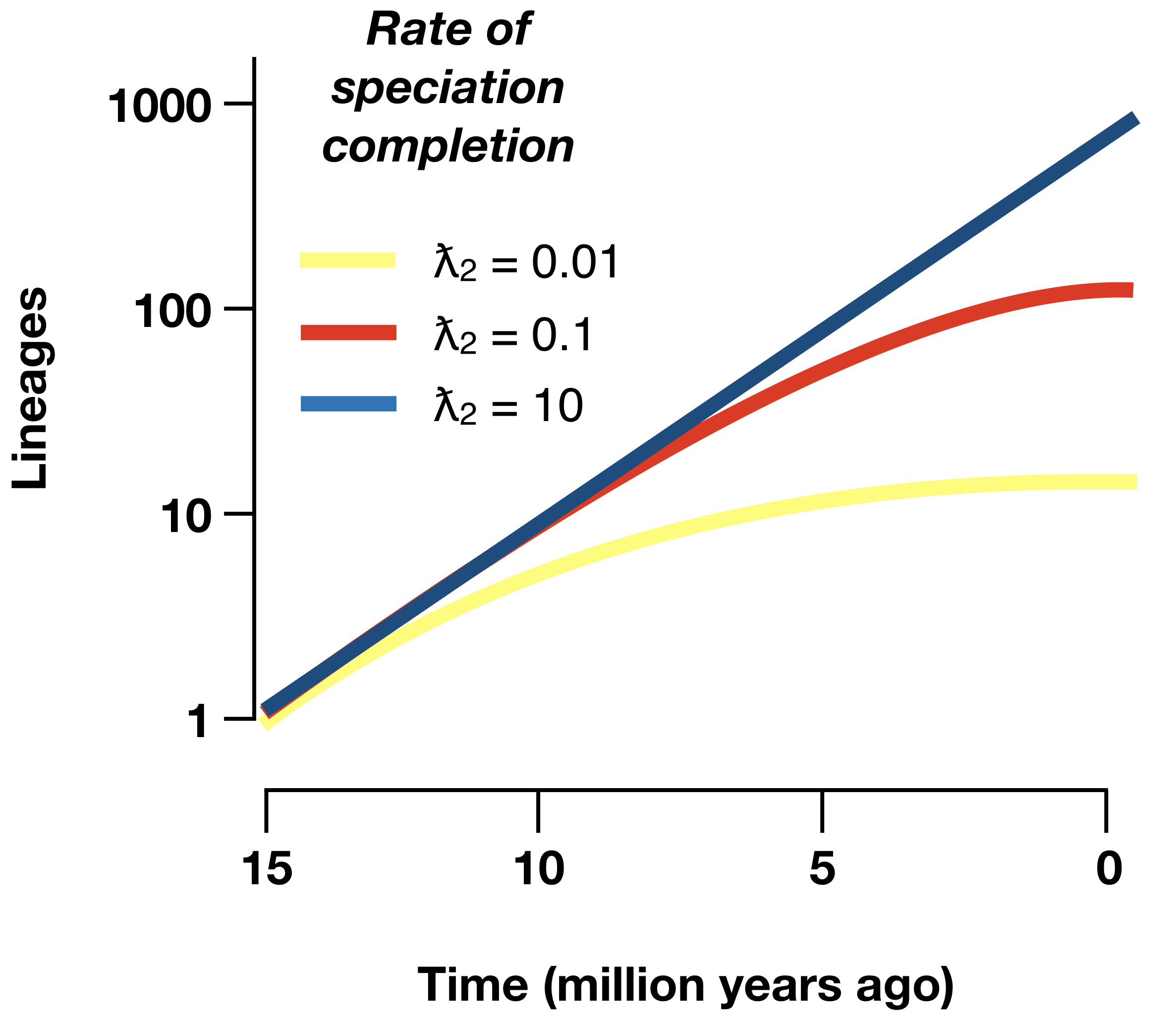
Se dispone de enfoques de verosimilitud para este modelo de especiación prolongada. Nuevamente, la verosimilitud debe calcularse mediante métodos numéricos (Lambert et al. 2015). Ajustando este modelo al árbol de salamandra, obtenemos una máxima capacidad logarítmica de 513.8 con valores de parámetros λ 1 = 0.059, λ 2 = 0.44 y μ = 0.0. Esto corresponde a una puntuación AIC de -1021.6; este modelo se ajusta tanto como el mejor de los modelos variables en el tiempo, pero no así como el modelo dependiente de la diversidad considerado anteriormente. De nuevo, sin embargo, no estoy incluyendo combinaciones plausibles de modelos, como la especiación prolongada que varía a través del tiempo.
Hasta ahora, los modelos de especiación prolongada permanecen principalmente en el ámbito de la teoría neutra ecológica, y apenas están comenzando a pasar a la filogenética y la biología evolutiva (ver, por ejemplo, Sukumaran y Lacey Knowles 2017). Sin embargo, creo que los modelos que tratan a la especiación como un proceso que lleva tiempo —más que algo instantáneo— serán una adición importante a nuestra caja de herramientas macroevolutivas en el futuro.


