13.2: Un Modelo de Diversificación Dependiente del Estado
- Page ID
- 54314
Los modelos que consideraremos en este capítulo incluyen la evolución de rasgos y la diversificación de linajes asociados. En el caso más simple, podemos considerar un modelo donde el personaje tiene dos estados, 0 y 1, y las tasas de diversificación dependen de esos estados. Necesitamos modelar las transiciones entre estos estados, lo que podemos hacer de manera idéntica a lo que hicimos en el Capítulo 7 usando un modelo de Markov en tiempo continuo. Expresamos este modelo usando dos parámetros de velocidad, una tasa de avance q 01 y una tasa hacia atrás q 10.
Consideramos ahora la idea de que las tasas de diversificación pueden depender del estado del carácter. Suponemos que las especies con estado de carácter 0 tienen una cierta tasa de especiación (λ 0) y tasa de extinción (μ 0), y que las especies en 1 tienen tasas potencialmente diferentes tanto de especiación (λ 1) como de extinción (μ 1 ). Es decir, cuando el personaje evoluciona, afecta la tasa de especiación y/o extinción de los linajes. Así, tenemos un modelo de seis parámetros (Maddison et al. 2007). Suponemos que los linajes padres dan a luz a hijas con el mismo estado de carácter, es decir, que los estados de carácter no cambian en la especiación.
Es sencillo simular la evolución bajo nuestro modelo de diversificación dependiente del estado. Procedemos de la misma manera que lo hicimos para los modelos de nacimiento-muerte, dibujando tiempos de espera, pero estos tiempos de espera pueden ser tiempos de espera para el siguiente cambio de estado de personaje, especiación o evento de extinción. En particular, imagine que hay n linajes presentes en el tiempo t, y que k de estos linajes están en el estado 0 (y n − k están en el estado 1). El tiempo de espera para el siguiente evento seguirá una distribución exponencial con un parámetro de tasa de:
\[ρ = k(q_{01} + λ_0 + μ_0)+(n − k)(q_{10} + λ_1 + μ_1) \label{13.1}\]
Esta ecuación dice que la tasa total de eventos es la suma de los eventos que pueden suceder a linajes con estado 0 (cambio de estado a 1, especiación o extinción) y los eventos análogos que pueden suceder a linajes con estado 1. Una vez que tenemos un tiempo de espera, podemos asignar un tipo de evento dependiendo de las probabilidades. Por ejemplo, la probabilidad de que el evento sea un cambio de estado de carácter de 0 a 1 es:
\[p_{q_{01}} = (n ⋅ q_{01})/ρ\label{13.2}\]
Y la probabilidad de que el evento sea la extinción de un linaje con estado de carácter 1 es:
\[p_{μ_1} = \dfrac{(n − k)⋅μ_1}{ρ} \label{13.3}\]
Y así sucesivamente para los otros cuatro posibles eventos.
Una vez que hayamos elegido un evento de esta manera, podemos asignarlo aleatoriamente a uno de los linajes en el estado apropiado, siendo cada linaje igualmente probable que sea elegido. Luego procedemos hacia adelante en el tiempo hasta que tengamos un conjunto de datos con el tamaño deseado o profundidad de tiempo total.
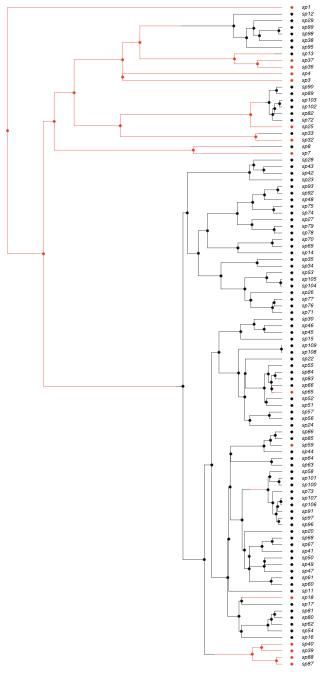
Un ejemplo de simulación se muestra en la Figura 13.1. Como puede ver, bajo estos parámetros del modelo el impacto de los estados de carácter en la diversificación es fácilmente evidente. En la siguiente sección descubriremos cómo extraer esa información de nuestros datos.