13.3: Cálculo de probabilidades para modelos de diversificación dependientes del Estado
- Page ID
- 54262
Para calcular probabilidades de modelos de diversificación dependientes del estado, utilizamos un algoritmo de poda con cálculos que retroceden a través del árbol desde las puntas hasta la raíz. Seguiremos la descripción de este algoritmo en Maddison et al. (2007). Ya hemos utilizado este enfoque para derivar probabilidades de modelos de nacimiento-muerte de tasa constante en árboles (Capítulo 12), y esta derivación es similar.
Consideramos un árbol filogenético con datos sobre los estados de carácter en las puntas. A los efectos de este ejemplo, asumiremos que el árbol está completo y correcto —no nos falta ninguna especie, y no hay incertidumbre filogenética. Volveremos a estos dos supuestos más adelante en el capítulo.
Necesitamos obtener la probabilidad de obtener los datos dado el modelo (la verosimilitud). Como hemos visto antes, calcularemos esa probabilidad retrocediendo en el tiempo usando un algoritmo de poda (Maddison et al. 2007). El principio clave, de nuevo, es que si conocemos las probabilidades en algún momento en el árbol, podemos calcular esas probabilidades en algún momento inmediatamente anterior. Al aplicar este método sucesivamente, podemos retroceder hacia la raíz del árbol. Nos movemos hacia atrás a lo largo de cada rama del árbol, fusionando estos cálculos en los nodos. Cuando llegamos a la raíz, tenemos la probabilidad de los datos dado el modelo y todo el árbol —es decir, tenemos la probabilidad.
La otra pieza esencial es que tengamos un punto de partida. Cuando empezamos en las puntas del árbol, asumimos que nuestros estados de carácter son fijos y conocidos. Utilizamos el hecho de que conocemos todas las especies y sus estados de carácter en la actualidad como nuestro punto de partida, y retrocedemos desde allí (Maddison et al. 2007). Por ejemplo, para una especie con estado de carácter 0, la probabilidad para el estado 0 es 1, y para el estado 1 es cero. Es decir, en las puntas del árbol podemos iniciar nuestros cálculos con una probabilidad de 1 para el estado que coincide con el estado de punta, y 0 en caso contrario.
Esta discusión también destaca el hecho de que incorporar incertidumbre y/o variación en los estados de punta para estos algoritmos no es computacionalmente difícil, solo necesitamos partir de un punto diferente en las puntas. Por ejemplo, si no estamos completamente seguros sobre el estado de punta para ciertos taxones, podemos comenzar con probabilidades de 0.5 para comenzar en el estado 0 y 0.5 para comenzar en el estado 1. Sin embargo, tales cálculos no se implementan comúnmente en software de métodos comparativos.
Ahora necesitamos considerar el cambio en la probabilidad a medida que retrocedemos en el tiempo en el árbol (Maddison et al. 2007). Consideraremos algún intervalo de tiempo muy pequeño Δ t, y posteriormente usaremos ecuaciones diferenciales para averiguar qué sucede en el límite ya que este intervalo va a cero (Figura 13.2). Dado que eventualmente tomaremos el límite como Δ t → 0, podemos suponer que el intervalo de tiempo es tan pequeño que, a lo sumo, un evento (especiación, extinción o cambio de carácter) ha ocurrido en ese intervalo, pero nunca más de uno. Calcularemos la probabilidad de los datos observados dado que el carácter se encuentra en cada estado en el tiempo t, nuevamente midiendo el tiempo hacia atrás desde la actualidad. Es decir, estamos considerando la probabilidad de los datos observados si, en el tiempo t, el estado del carácter estaba en el estado 0 [p 0 (t)] o el estado 1 [p 1 (t)]. Por ahora, podemos suponer que conocemos estas probabilidades, e intentar calcular probabilidades actualizadas en algún momento anterior t + Δ t: p 0 (t + Δ t) y p 1 (t + Δ t).
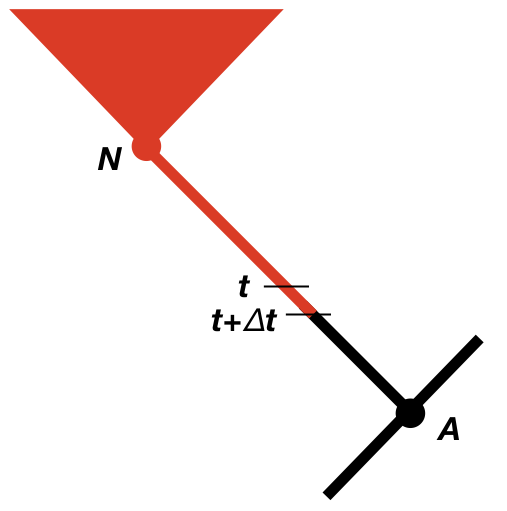
Para calcular p 0 (t + Δ t) y p 1 (t + Δ t), consideramos todas las cosas posibles que podrían suceder en un intervalo de tiempo Δ t a lo largo de una rama en a árbol filogenético que son compatibles con nuestro conjunto de datos (Figura 13.2; Maddison et al. 2007). Primero, nada pudo haber pasado; segundo, nuestro estado de carácter podría haber cambiado; y tercero, podría haber habido un evento de especiación. Este último evento puede parecer incorrecto, ya que solo estamos considerando cambios a lo largo de las ramas del árbol y no en los nodos. Si no reconstruimos ningún evento de especiación en algún momento a lo largo de una rama, entonces ¿cómo podría haber ocurrido uno? La respuesta es que podría haber ocurrido un evento de especiación pero todos los taxones que descienden de esa rama se han extinguido desde entonces. También debemos considerar la posibilidad de que el linaje derecho o izquierdo se extinga después del evento de especiación; es por ello que las probabilidades de eventos de especiación aparecen dos veces en la Figura 13.2 (Maddison et al. 2007).
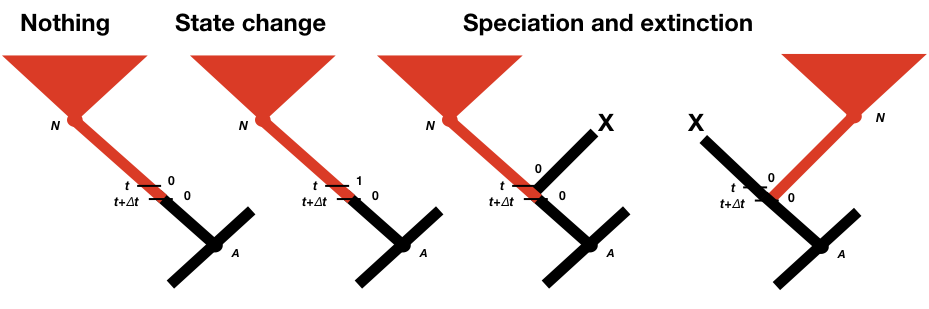
Podemos escribir una ecuación para estas probabilidades actualizadas. Consideraremos la probabilidad de que el carácter esté en el estado 0 en el tiempo t + Δ t; la ecuación para el estado 1 es similar (Maddison et al. 2007).
\[ \begin{aligned} p_0 (t+\Delta t)=(1-\mu_0 )\Delta t \cdot [(1-q_{01} \Delta t)(1-\lambda_0 \Delta t) p_0 (t)+q_{01} \Delta t(1-\lambda_0 \Delta t) \\ p_1 (t)+2 \cdot (1-q_{01} \Delta t) \lambda_0 \Delta t \cdot E_0 (t) p_0 (t)] \end{aligned} \label{13.4}\]
Podemos multiplicar y simplificar. También dejaremos caer cualquier término que incluya [Δ t] 2, que se vuelve increíblemente pequeño a medida que Δ t disminuye. Haciendo eso, obtenemos (Maddison et al. 2007):
\[p_0(t + Δt)=[1 − (λ_0 + μ_0 + q_{01})Δt]p_0(t)+(q_{01}Δt)p_1(t)+2(λ_0Δt)E_0(t)p_0(t) \label{13.5}\]
Del mismo modo,
\[p_1(t + Δt)=[1 − (λ_1 + μ_1 + q_{10})Δt]p_1(t)+(q_{10}Δt)p_0(t)+2(λ_1Δt)E_1(t)p_1(t) \label{13.6}\]
Entonces podemos encontrar la tasa instantánea de cambio para estas dos ecuaciones resolviendo para p 1 (t + Δ t)/[Δ t], luego tomando el límite como Δ t → 0. Esto da (Maddison et al. 2007):
\[ \frac{dp_0}{dt} = -(\lambda_0 + \mu_0 + q_{01}) p_0(t) + q{01}p_1(t) + 2 \lambda_0 E_0(t) p_0(t) \label{13.7}\]
y:
\[ \frac{dp_1}{dt} = -(\lambda_1 + \mu_1 + q_{10}) p_1(t) + q{10}p_1(t) + 2 \lambda_1 E_1(t) p_1(t) \label{13.8}\]
También debemos considerar E 0 (t) y E 1 (t). Estos representan la probabilidad de que un linaje con estado 0 o 1, respectivamente, y vivo en el tiempo t se extinga antes del día de hoy. Despreciando la derivación de estas fórmulas, que se pueden encontrar en Maddison et al. (2007) y está estrechamente relacionado con términos similares en los Capítulos 11 y 12, tenemos:
\[ \frac{dE_0}{dt} = \mu_0-(\lambda_0+\mu_0+q_{01} ) E_0 (t)+q_{01} E_1 (t)+\lambda_0 [E_0 (t)]^2 \label{13.9} \]
y:
\[ \frac{dE_1}{dt} = \mu_1-(\lambda_1+\mu_1+q_{10} ) E_1 (t)+q_{10} E_0 (t)+\lambda_1 [E_1 (t)]^2 \label{13.10}\]
A lo largo de una sola rama en un árbol, podemos sumar muchos intervalos de tiempo tan pequeños. Pero, ¿qué pasa cuando llegamos a un nodo? Bueno, si consideramos el intervalo de tiempo que contiene el nodo, entonces ya sabemos lo que pasó —un evento de especiación. También sabemos que las dos hijas inmediatamente después del evento de especiación fueron idénticas en sus rasgos (esto es una suposición del modelo). Así podemos calcular la probabilidad para su antepasado para cada estado como producto de las probabilidades de que las dos ramas hijas entren en ese nodo y la tasa de especiación (Maddison et al. 2007). De esta manera, fusionamos nuestros cálculos de verosimilitud a lo largo de cada rama cuando llegamos a los nodos del árbol.
Cuando llegamos a la raíz del árbol, casi terminamos — ¡pero no del todo! Tenemos cálculos de verosimilitud parcial para cada estado de carácter —así sabemos, por ejemplo, la probabilidad de los datos si hubiéramos comenzado con un estado raíz de 0, y también si hubiéramos comenzado en 1. Para fusionarlos necesitamos usar probabilidades de cada estado de carácter en la raíz del árbol (Maddison et al. 2007). Por ejemplo, si no conocemos el estado raíz de cualquier información externa, podríamos considerar que las probabilidades de raíz para cada estado son iguales, 0.5 para el estado 0 y 0.5 para el estado 1. Luego multiplicamos la probabilidad asociada a cada estado con la probabilidad raíz para ese estado. Finalmente, sumamos estas probabilidades juntas para obtener la plena probabilidad de los datos dado el modelo.
La cuestión de qué probabilidades de raíz utilizar para este cálculo ha sido discutida en la literatura, y sí importa en algunas aplicaciones. Aparte de probabilidades iguales de cada estado, otras opciones incluyen usar información externa para informar probabilidades previas sobre cada estado (por ejemplo, Hagey et al. 2017), encontrar la frecuencia de equilibrio calculada de cada estado bajo el modelo (Maddison et al. 2007), o ponderar cada raíz estado por su probabilidad de generar los datos, tratando efectivamente la raíz como un parámetro de molestia (FitzJohn et al. 2009).
He descrito la situación en la que tenemos dos estados de carácter, pero este método generaliza bien a los caracteres multiestado (el método MusSe; FitzJohn 2012). Podemos describir la evolución del personaje de la misma manera que se describe para los caracteres discretos multiestado en el capítulo 9. Entonces podemos asignar parámetros únicos de tasa de diversificación a cada uno de los k estados de carácter: λ 0, λ 1,..., λ k y μ 0, μ 1,..., μ k (FitzJohn 2012). Sin embargo, vale la pena tener en cuenta que no es demasiado difícil construir un modelo donde los parámetros no sean identificables y la adaptación y estimación del modelo se vuelvan muy difíciles.


