13.4: ML y Pruebas Bayesianas para Diversificación Dependiente del Estado
- Page ID
- 54285
Ahora que podemos calcular la probabilidad para los modelos de diversificación dependientes del estado, la formulación de pruebas ML y Bayesianas sigue el mismo patrón que hemos encontrado antes. Para ML, algunas comparaciones están anidadas y así puedes usar pruebas de relación de verosimilitud. Por ejemplo, podemos comparar el modelo completo de BiSSE (Maddison et al. 2007), con los parámetros q 01, q 10, λ 0, λ 1, μ 0, μ 1 con a modelo restringido con parámetros q 01, q 10, λ a l l, μ a l l. Dado que el modelo restringido es un caso especial del modelo completo donde λ 0 = λ 1 = λ a l l y μ 0 = μ 1 = μ a l l, podemos comparar los dos usando una prueba de razón de verosimilitud, como se describió anteriormente en el libro. Alternativamente, podemos comparar una serie de modelos tipo Bisse comparando sus puntuaciones A I C c.
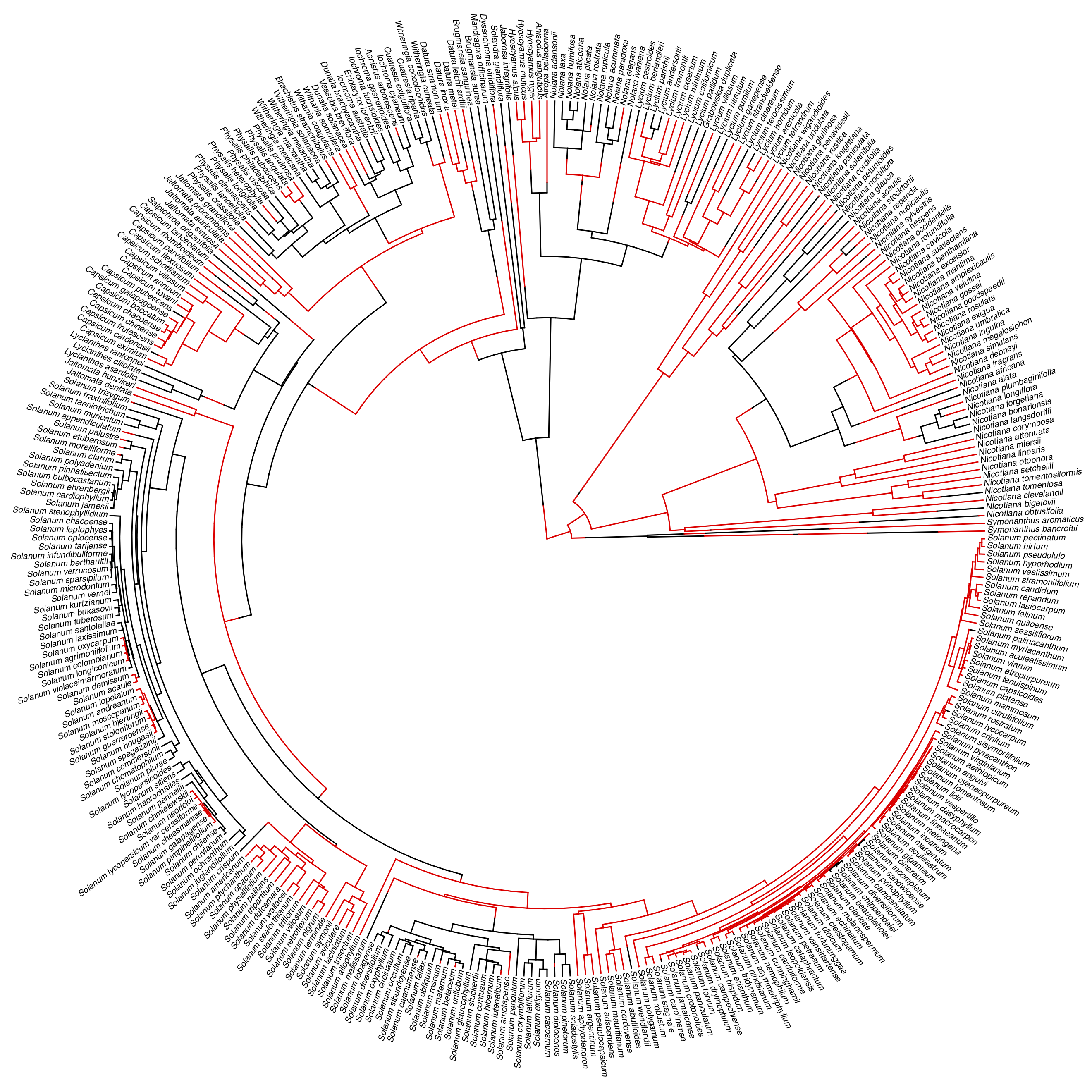
Por ejemplo, voy a aplicar este enfoque al ejemplo de autoincompitabilidad. Utilizaré datos de Goldberg e Igic (2012), quienes proporcionan un árbol filogenético y datos para 356 especies de Solanáceas. Todas las especies se clasificaron como de alguna forma de autoincompatibilidad, aunque el estado sea variable entre las poblaciones. Los datos, junto con un mapa de caracteres estocástico de cambios de estado, se muestran en la Figura 13.4. Aplicando los modelos BiSSE a estos datos y asumiendo que q 01 ≠ q 10, obtenemos los siguientes resultados:
| Modelo | Número de parámetros | Estimaciones de parámetros | LnL | AIC |
|---|---|---|---|---|
| Modelo independiente del personaje | 4 | λ = 0.65, μ = 0.57 | -945.96 | 1899.9 |
| q 01 = 0.16, q 10 = 0.09 | ||||
| La tasa de especiación depende del carácter | 5 | μ = 0.57 | -945.57 | 1901.1 |
| λ 0 = 0.69, λ 1 = 0.63 | ||||
| q 01 = 0.17, q 10 = 0.08 | ||||
| La tasa de extinción depende del carácter | 5 | λ = 0.65 | -943.93 | 1897.9 |
| μ 0 = 0.45, μ 1 = 0.67 | ||||
| q 01 = 0.22, q 10 = 0.06 | ||||
| Modelo completo dependiente del carácter | 6 | λ 0 = 0.49, λ 1 = 0.79 | -941.94 | 1895.9 |
| μ 0 = 0.20, μ 1 = 0.84 | ||||
| q 01 = 0.29, q 10 = 0.05 |
A partir de esto, concluimos que los modelos donde el personaje influye en la diversificación encajan mejor, siendo el modelo completo el que más soporte recibe. No podemos descontar la posibilidad de que el personaje solo influya en la extinción y no en la especiación, ya que ese modelo está dentro de 2 unidades AIC del mejor modelo.
Alternativamente, podemos realizar una prueba bayesiana para la diversificación dependiente del estado.
Prueba bayesiana para diversificación dependiente del estado
Al igual que otros modelos del libro, esto requiere configurar un algoritmo MCMC que muestree las distribuciones posteriores de los parámetros de nuestro modelo (FitzJohn 2012). En este caso:
- Muestrear un conjunto de valores de parámetros iniciales, q 01, q 10, λ 0, λ 1, μ 0, μ 1, a partir de sus distribuciones anteriores. Por ejemplo, se podría establecer la distribución previa para todos los parámetros como exponencial con una media y varianza de λ p r i o r i (tenga en cuenta que, como de costumbre, la elección para este parámetro debe depende de las unidades de longitud de rama de árbol que esté utilizando). Luego seleccionamos valores iniciales para todos los parámetros del anterior.
- Dados los valores actuales de los parámetros, seleccione nuevos valores de parámetros propuestos utilizando la densidad propuesta Q (p ′| p). Para todos los valores de parámetros, podemos usar una densidad de propuesta uniforme con ancho w p, de modo que Q (p ′| p) U (p − w p /2, p + w p /2). Podemos elegir todos los valores de los parámetros simultáneamente, o uno a la vez (este último suele ser más efectivo).
- Calcula tres proporciones:
- El ratio de probabilidades anterior. Esta es la relación de la probabilidad de dibujar los valores de los parámetros p y p′ del anterior. Como tenemos antecedentes exponenciales para todos los parámetros, podemos calcular esta relación como:\ [R_ {prior} =\ frac {\ lambda_ {prior_i} e^ {-\ lambda_ {prior_i} p'}} {\ lambda_ {prior_i} e^ {-\ lambda_ {prior_i} p} =e^ {\ lambda_ {prior_i} (p-p')}\ etiqueta {13.11}\ [
- La relación de densidad propuesta. Esta es la relación de probabilidad de propuestas que van de p a p ′ y a la inversa. Ya hemos declarado una densidad simétrica de propuesta, de manera que Q (p ′| p) = Q (p | p ′) y R p r o p o s a l = 1.
- La razón de verosimilitud Esta es la relación de probabilidades de los datos dados los dos valores de parámetros diferentes. Podemos calcular estas probabilidades a partir del enfoque descrito en el apartado anterior.
- Encuentre R a c c e p t como el producto de las probabilidades previas, la relación de densidad propuesta y la razón de verosimilitud. En este caso, la relación de densidad propuesta es 1, por lo que (eq. 13.12):
R a c c e p t = R p r i o r ⋅ R l i k e l i h o o d


