16.8: Formulación Lotka-Volterra

Última actualización
Guardar como PDF

Page ID: 53268

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Las ecuaciones de competencia generalmente se presentan en los libros de texto como el modelo de competencia Lotka—Volterra. Esto apareció por primera vez en la literatura ecológica en la década de 1920 y se define no solo en términos de las interacciones entre especies, sino también en términos de las capacidades de carga de las especies, de la siguiente manera.

Screen Shot 2019-11-09 en 3.52.27 PM.png

\[\frac{1}{N_1}\frac{dN_1}{dt}\,=\,r_1(1-\frac{N_1+a_{1,2}N_2}{K_1})\]

\[\frac{1}{N_2}\frac{dN_2}{dt}\,=\,r_2(1-\frac{N_2+a_{2,1}N_1}{K_2})\]

\(K_1\)y\(K_2\) son las capacidades de carga para las especies 1 y 2, respectivamente. Parámetros\(a_{1,2}\) y\(a_{2,1}\) representan la interferencia de cada especie sobre la otra. Si\(a_{1,2}=2\), por ejemplo, cada individuo de la Especie 2 interfiere con el crecimiento de la Especie 1 como si se tratara de dos individuos de la Especie 1. Si, por otro lado\(a_{1,2}=1/2\), se necesitan dos individuos de la Especie 2 para tener el mismo efecto negativo en el crecimiento de la Especie 1 que un individuo de la Especie 1 misma.

Para comparar esto con la formulación RSN, representar las Ecuaciones 16.7.1 y 16.7.2 con\(i\) y\(j\) subíndices

\(\frac{1}{N_i}\frac{dN_i}{dt}\,=\,r_i(1-\frac{N_i+a_{i,j}N_j}{K_i})\)

y multiplicar el lado derecho por\(r_i\),

\(\frac{1}{N_i}\frac{dN_i}{dt}\,=\,r_i\,-\frac{r_i}{K_i}N_i\,-\frac{a_{i,j}r_i}{K_i}N_j\)

Esto demuestra que la formulación Lotka—Volterra es isomórfica a la formulación RSN. Todas las conclusiones sobre los sistemas competitivos examinadas hasta ahora se aplican también a la formulación Lotka—Volterra, con la traducción adecuada de los parámetros. El parámetro\(r_i\) es el mismo tanto en la formulación Lotka—Volterra como en la formulación RSN, pero\(s_{i,i}= −r_i/K_i\) y\(s_{i,j}=−a_{i,j}r_i/K_i\).

Sin embargo, tenga cuidado con una afirmación ampliamente citada derivada de esta formulación que aparece a lo largo de la literatura y libros de texto ecológicos. Declaraciones como “La convivencia requiere que cada especie se inhiba más de lo que inhibe a las otras especies” abundan en los libros de texto y en la literatura ecológica. Por ay, esas afirmaciones no son correctas.

caja\(\PageIndex{2}\)

La coexistencia en el modelo Lotka—Volterra requiere que cada especie pueda aumentar desde bajas densidades cuando la otra especie se encuentra en su equilibrio de especie única.

Para ver esto, examine la Figura 16.21. Aquí la Especie 1 se inhibe con s ₁₁ =−1, mientras que inhibe más fuertemente a las otras especies con s ₁₂ =−1.153. Sin embargo, existe una convivencia global. Evidentemente, la convivencia no requiere que cada especie se inhiba más de lo que inhibe a la otra, como en la sabiduría convencional. La confusión en la literatura aparentemente ha surgido de la presencia de los términos de capacidad de carga, K ₁ y K ₂, en la formulación Lotka—Volterra. Estos términos oscurecen los efectos de los términos de interacción, a _1,2 y a _2,1, cuando las capacidades de carga difieren entre las especies.

¿Qué, entonces, es una afirmación correcta sobre la convivencia? Se puede poner en términos de aumentar a partir de bajas densidades, como se muestra en Box\(\PageIndex{2}\). Se requiere la frase calificativa “a partir de densidades bajas”, ya que las especies no presentes pueden aumentar de altas densidades en un sistema biestable, como en la Figura 16.20, y flotarla al otro estado, aunque no pueda darse coexistencia.

Otra forma en la que se ha explicado la convivencia es por Vandermeer (1981 Bioscience), conectando la convivencia con cierto tipo de “sobrerendimiento”, donde dos cultivos requieren menos tierra para la misma productividad anual cuando crecen juntos que cuando crecen separados.

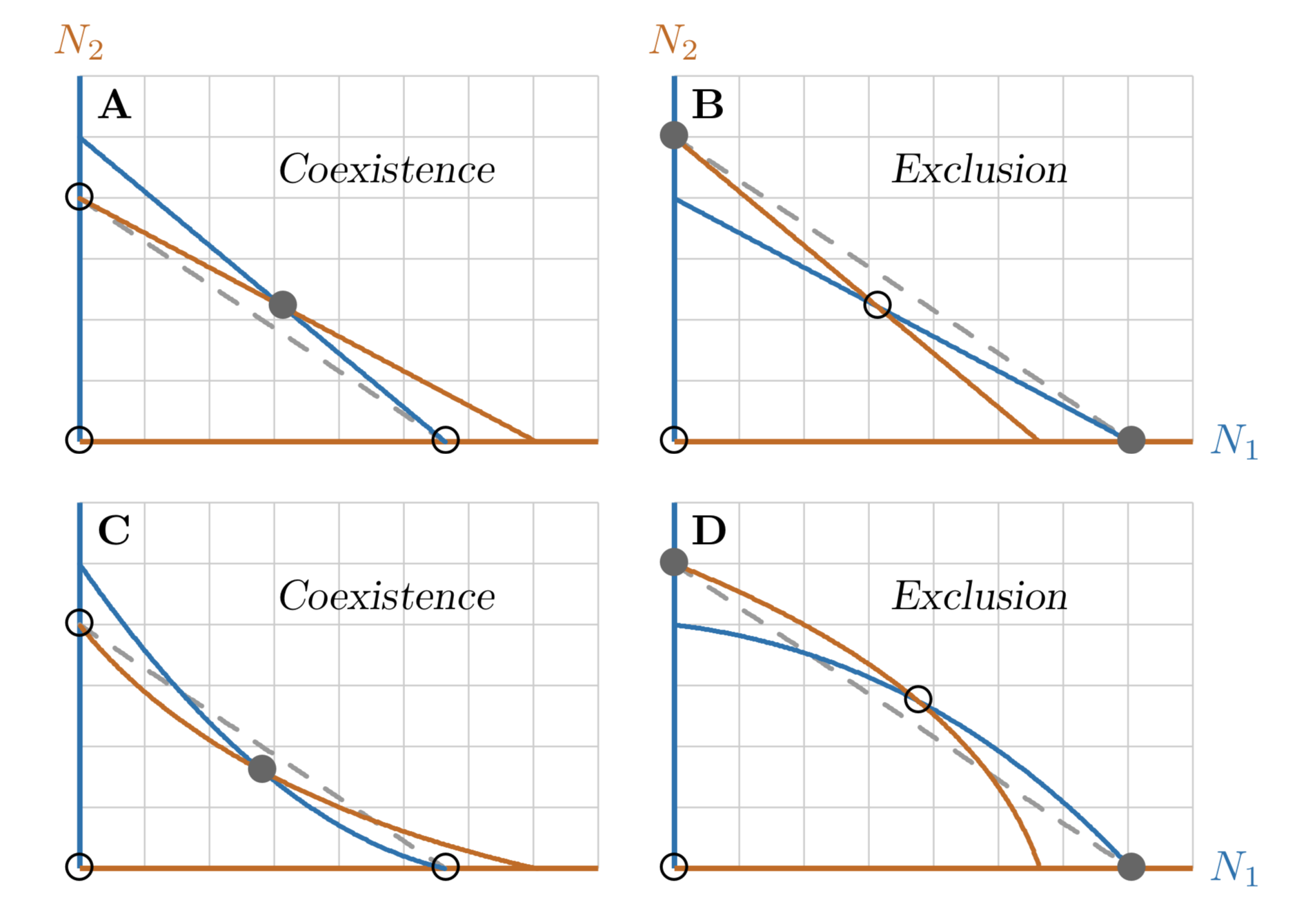
Screen Shot 2019-11-09 en 3.53.43 PM.png

La prueba es si el equilibrio articular está por encima de una línea que conecta los equilibrios de una sola especie (gris discontinuo en la Figura\(\PageIndex{3}\) A) o por debajo de la línea (Figura\(\PageIndex{3}\) B).

Esta vista es correcta para los modelos que hemos estado considerando con isoclinas de línea recta, pero incorrecta para modelos más generales con isoclinas curvas (Figura\(\PageIndex{3}\) C, D). El enunciado en Box\(\PageIndex{2}\), sin embargo, es cierto en cada uno de estos casos.

Todas las cosas consideradas, en lugar de depender de reglas generales, puede ser mejor evaluar un sistema directamente, por ejemplo con los métodos de vectores propios y valores propios descritos en el Capítulo 10.