8: La respuesta a la selección fenotípica
- Page ID
- 58065
La evolución por selección natural requiere:
- Variación en un fenotipo
- Esa supervivencia y reproducción no es aleatoria con respecto a esta variación fenotípica.
- Que esta variación es heredable.
Los puntos 1 y 2 encapsulan nuestra idea de Selección Natural, pero la evolución por selección natural solo ocurrirá si también se cumple la 3ra condición. Es la naturaleza heredable de la variación que las parejas cambian dentro de una generación debido a la selección natural para cambiar a través de las generaciones (cambio evolutivo).
Empecemos pensando en el cambio dentro de una generación debido a la selección direccional, donde la selección actúa para cambiar el fenotipo medio dentro de una generación. Por ejemplo, una disminución en la altura media dentro de una generación, debido a que los organismos más altos tienen una menor probabilidad de sobrevivir a la reproducción que los organismos más cortos. Específicamente, denotaremos nuestro fenotipo medio en la reproducción por\(\mu_S\), es decir, después de que la selección haya actuado, y nuestro fenotipo medio antes de la selección actúa por\(\mu_{BS}\). Esta segunda cantidad puede ser difícil de medir, ya que obviamente la selección actúa a lo largo del ciclo de vida, por lo que podría ser más fácil pensar en esto como el fenotipo medio si la selección no hubiera actuado. Entonces el cambio en el fenotipo medio dentro de una generación es\(\mu_{S} - \mu_{BS}= S\), llamaremos\(S\) al diferencial de selección.
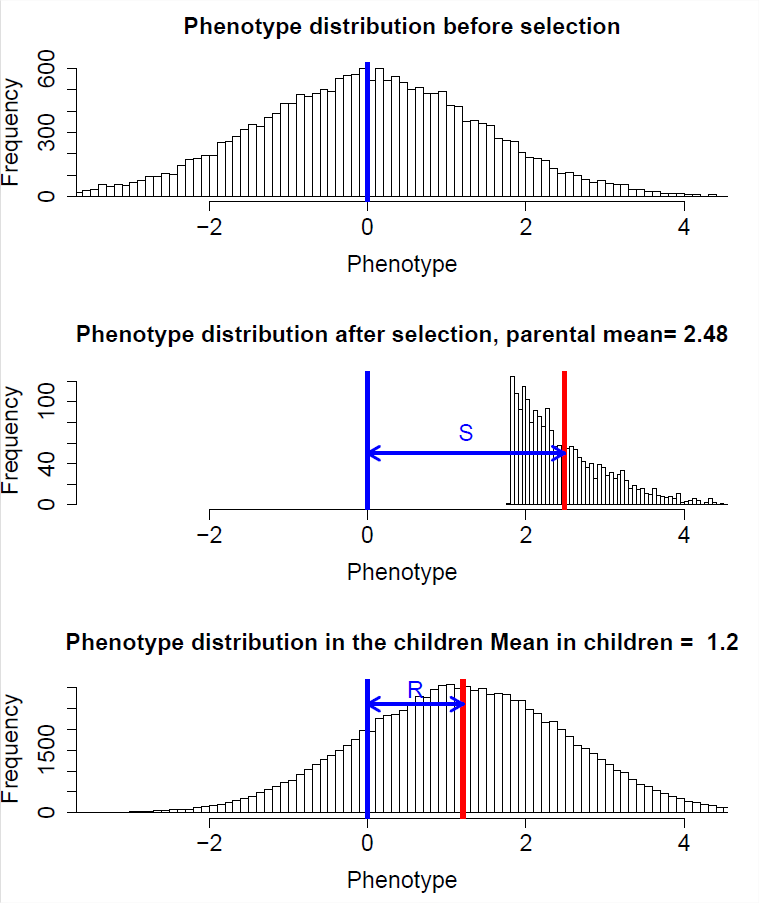
Nos interesa predecir la distribución de fenotipos en la próxima generación. En particular, nos interesa el fenotipo medio en la próxima generación para entender cómo la selección direccional ha contribuido al cambio evolutivo. Denotaremos el fenotipo medio en la descendencia, es decir, el fenotipo medio en la siguiente generación antes de que actúe la selección, como\(\mu_{NG}\). Al cambio a través de generaciones llamaremos la respuesta a la selección\(R\) y pondremos esto igual a\(\mu_{NG}- \mu_{BS}\).
El fenotipo medio en la próxima generación es
\[\mu_{NG} = \E \left( \mathbb{E}(X_{kid} | X_{mum},X_{dad}) \right)\]
donde la expectativa interna nos está dando el fenotipo esperado del niño dado a los padres, y la expectativa externa es sobre posibles emparejamientos de padres formados por individuos que se aparean aleatoriamente que sobreviven para reproducirse. Podemos usar la ecuación\ ref {predict_kid} para obtener una expresión para esta expectativa:
\[\mu_{NG} = \mu_{BS} + \beta_{mid,kid} ( \mathbb{E}(X_{mid}) - \mu_{BS})\]
Entonces para obtener\(\mu_{NG}\) necesitamos calcular\(\mathbb{E}(X_{mid})\), el fenotipo esperado de punto medio de pares de individuos que sobreviven para reproducirse. Este es solo el fenotipo esperado en los individuos que sobrevivieron para reproducirse (\(\mu_{S}\)), por lo que
\[\mu_{NG} = \mu_{BS} + h^2 (\mu_S - \mu_{BS})\]
Así podemos escribir nuestra respuesta a la selección como
\[R = \mu_{NG} -\mu_{BS} = h^2 (\mu_S - \mu_{BS}) = h^2 S \label{breeders_eqn}\]
Entonces nuestra respuesta a la selección es proporcional a nuestro diferencial de selección, y la constante de proporcionalidad es la heredabilidad de sentido estrecho. Esta ecuación a veces se le conoce como la ecuación del Obtentor. Es una afirmación de que el cambio evolutivo a través de generaciones (\(R\)) es proporcional al cambio causado por la selección direccional dentro de una generación (\(S\)), y que la fuerza de esta relación está determinada por la heredabilidad de sentido estrecho ( \(h^2\)).
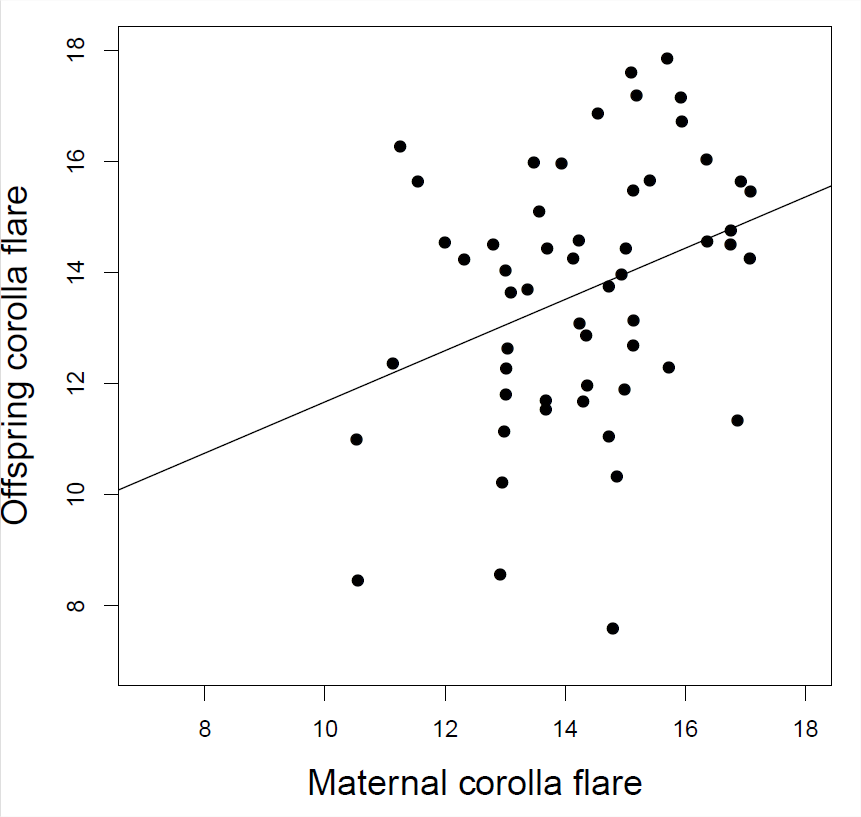
Galeno exploró la selección en forma de flor en Polemonium viscosum. Encontró que las plantas con una llamarada de corola más grande tuvieron más visitas de abejorros, lo que resultó en un mayor conjunto de semillas y un\(17\%\) aumento en la llamarada de corola en las plantas contribuyendo a la siguiente generación. Con base en los datos del subtítulo de Figura\ ref {fig:Galen_corolla} ¿cuál es la respuesta esperada en la próxima generación?

Si sabemos\(R\) y\(S\) podemos estimar\(h^2\). Las heredabilidades estimadas así se denominan 'herencia realizada'. Las estimaciones de la “herencia realizada” se pueden producir fácilmente en experimentos de selección artificial:
Del experimento mostrado en la Figura\ ref {fig:Illinois_LTS_Breeders_EQ}, el contenido medio de aceite de maíz en 1897 fue\(4.78\), entre los\(24\) individuos elegidos para reproducirse para la siguiente generación la media fue\(5.2\). La descendencia de estos individuos tuvo un contenido medio de aceite de semilla de\(5.1\). ¿Cuál es la heredabilidad realizada de sentido estrecho?
Para entender las bases genéticas de la respuesta a la selección, eche un vistazo a la Figura\ ref {fig:response_num_alleles}. La configuración es la misma que en nuestras figuras de simulación anteriores.

Los individuos que son seleccionados para formar nuestra próxima generación portan más alelos que incrementan el fenotipo en el rango actual de ambientes que vive actualmente la población. El individuo promedio antes de la selección portaba 100 de estos alelos 'up', mientras que la selección promedio individual sobreviviente lleva 108 alelos 'up'.
A medida que los individuos transmiten fielmente sus alelos a la siguiente generación el hijo promedio de los padres seleccionados lleva\(108\) alelos. Tenga en cuenta que la varianza ha cambiado poco, los niños tienen mucha variación en su genotipo, de tal manera que la selección puede impulsar fácilmente la evolución en las generaciones futuras. La frecuencia promedio de un alelo 'up' ha cambiado de\(50\%\) a\(54\%\). Las ganancias debidas a la selección se heredarán de manera estable a las generaciones futuras y se pueden combinar generación tras generación si las presiones de selección permanecieran constantes.
La respuesta a largo plazo a la selección
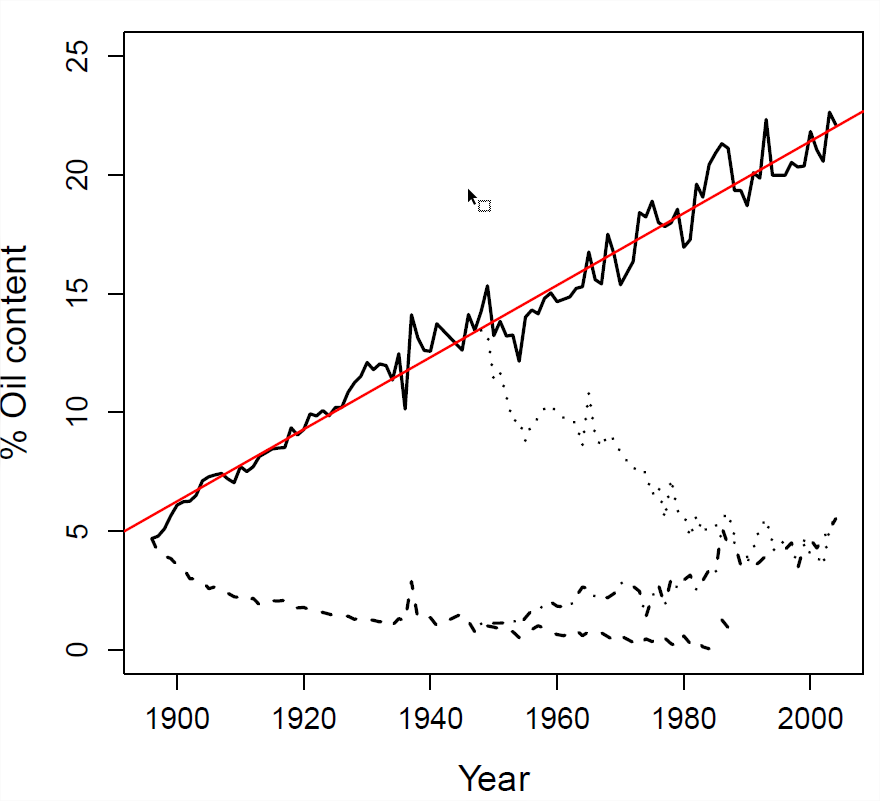
Ajuste lineal al experimento ascendente mostrado como una línea roja. Datos disponibles https://www.ideals.illinois.edu/handle/2142/3525, https://github.com/cooplab/popgen-no...orn/corn_LTS.R
Si nuestra presión de selección se mantiene a lo largo de muchas generaciones, podemos usar la ecuación de nuestro obtentor para predecir la respuesta. Si estamos dispuestos a asumir que nuestra heredabilidad no cambia y mantenemos un diferencial de selección constante (\(S\)), entonces después de\(n\) generaciones nuestra media de fenotipo habrá cambiado
\[n h^2 S\]
es decir, nuestra población mantendrá una respuesta lineal a la selección.
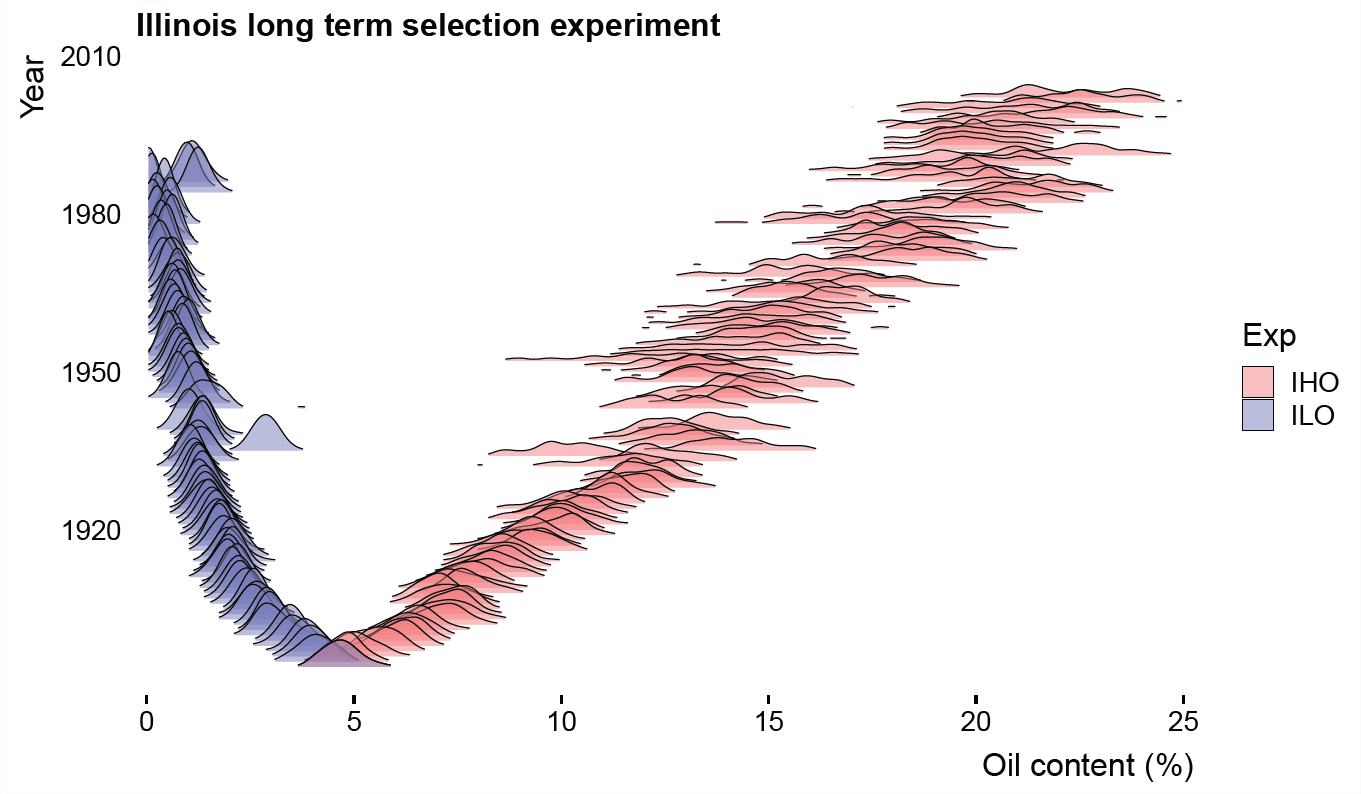
Por lo tanto, la selección consistente a largo plazo puede impulsar un cambio evolutivo impresionante. Un ejemplo de esto proviene de un experimento de campo en Illinois, donde los fitomejoradores han seleccionado sistemáticamente por mayor y menor contenido de aceite en maíz (ver nuestra anterior Figura\ ref {fig:Illinois_LTS_breeders_eq} para una generación de selección ascendente). Desde hace más de un siglo, han tomado semillas de las plantas en los extremos de la distribución y utilizándolas para formar la próxima generación. Han logrado impresionantes respuestas a largo plazo, empujando las distribuciones poblacionales mucho más allá de su rango inicial (Figura\ ref {fig:Illinois_LTS_DISTS}. Por ejemplo, la línea de selección ascendente de petróleo pasó de un contenido medio de aceite\(4.7\%\) en 1896 a\(22.1\%\) 2004. Han establecido dos poblaciones secundarias donde se invirtió el diferencial de selección. En la población de selección al alza han mantenido un incremento impresionantemente lineal en el contenido de petróleo, mostrado por la línea roja en la Figura\ ref {fig:Illinois_LTS_means}, pero mientras la respuesta es lineal al principio en la línea descendente pero rápidamente alcanzan un contenido de aceite muy bajo (limitado por el límite físico al 0% de contenido de petróleo).
Una población de ciervos rojos quedó atrapada en Jersey (una isla de Inglaterra) durante el último período interglacial. Del registro fósil podemos ver que la población se adaptó rápidamente a sus nuevas condiciones, tal vez debido a la selección para tiempos reproductivos más cortos en ausencia de depredación. En 6,000 años evolucionaron de un peso medio estimado de la población de 200 kg a un peso medio estimado de 36 kg (¡una reducción de 6 veces)! Se estima que el tiempo de generación del venado rojo es de 5 años y, a partir de una población actual, que la heredabilidad de sentido estrecho del fenotipo es de 0.5.
- Estimar el cambio medio por generación en el peso corporal medio.
- Estimar el cambio en el peso corporal medio causado por la selección dentro de una generación. Afirma tus suposiciones.
- Suponiendo que solo tenemos fósiles de la población fundadora y la población después de 6000 años, ¿debemos suponer que los cálculos reflejan con precisión lo que realmente ocurrió dentro de nuestra población?

Rosa {\ it Mammuthus exilis}. \ href {https://en.Wikipedia.org/wiki/Pygmy_...s_skeletal.png, CC BY 3.0.
En poblaciones silvestres, las presiones de selección rara vez se mantienen durante un gran número de generaciones. Por ejemplo, los Donantes han medido la selección fenotípica en Pinzones de Darwin durante varias décadas en la isla de Daphne Major. Han visto que las presiones de selección en el pinzón medio (Geospiza fortis) se han revertido varias veces a lo largo de los años (Figura\ ref {fig:Darwins_finches_unpred}).
Patrones de cambio fenotípico a largo plazo en la naturaleza
Mirando a través de la diversidad de plantas y animales vemos grandes cambios en tamaño y forma, ¿pueden las fortalezas de selección que podemos observar en cortos períodos de tiempo posiblemente explicar estos cambios?
Para comparar los cambios fenotípicos a lo largo de varios periodos de tiempo necesitamos alguna medida de la tasa de cambio fenotípico. propuso que la tasa de cambio de\(X_1\) a\(X_2\) en el intervalo de tiempo\(\Delta t\), medida en millones de años, se cuantifique como
\[\frac{\log \left(\frac{X_2}{X_1} \right) }{\Delta t} = \frac{\log \left(X_2 \right) -\log \left(X_1 \right) }{\Delta t}\]
expresando esto el log de la proporción, estamos viendo el cambio de pliegue proporcional, lo cual tiene sentido ya que un cambio evolutivo de 1cm de longitud es más impresionante si eres un ratón que un elefante. Al poner esto en una\(\log\) -escala estamos viendo el cambio relativo doble. llamado las unidades de esta medida `el Darwin ', con un cambio de Darwin correspondiente a un cambio de\(e\approx 2.71\) pliegue en un millón de años, un cambio de dos Darwin correspondiente a un \(e^2\approx 7.34\)veces cambio en un millón de años y así sucesivamente.
Calcula la tasa de cambio en la talla corporal en el Jersey ciervo rojo de Question\ ref {question:reddeer} en Darwins. Haga lo mismo para el cambio total en el contenido de aceite de maíz en las líneas ascendentes en la Figura\ ref {fig:Illinois_LTS_Means}.
examinó la tasa absoluta de cambio fenotípico en los datos de estudios de campo y el registro fósil, un conjunto de datos considerablemente expandido por. En la Figura\ ref {fig:uyeda_gingerich} cada punto es una observación de la evolución del fenotipo. El eje x muestra el periodo de tiempo en años durante los cuales se observó el cambio evolutivo, el eje x se graficó en una\(\log_{10}\) escala. El eje y muestra la tasa absoluta de cambio fenotípico, medida en Darwins, nuevamente en una\(\log_{10}\) escala.
En escalas de tiempo cortas vemos una evolución increíblemente rápida, tenga en cuenta las altas tasas a la izquierda de la Figura\ ref {fig:uyeda_gingerich}. Por ejemplo, el primer punto negro de la izquierda es un caso de evolución a lo largo de décadas en los cachorros caninos. La invasión del cangrejo verde (Carcinus maenas) impulsó la evolución de conchas más robustas en el buey canino atlántico (Nucella lapillus) en respuesta a la depredación a lo largo de la costa norteamericana. El grosor del labio de la concha de los crinos caninos en la población de St. Andrews, New Brunswick había cambiado de 0.94mm a 1.44mm en solo 25 años. Eso es un incremento del 50%, y una tasa de 17060 Darwins.
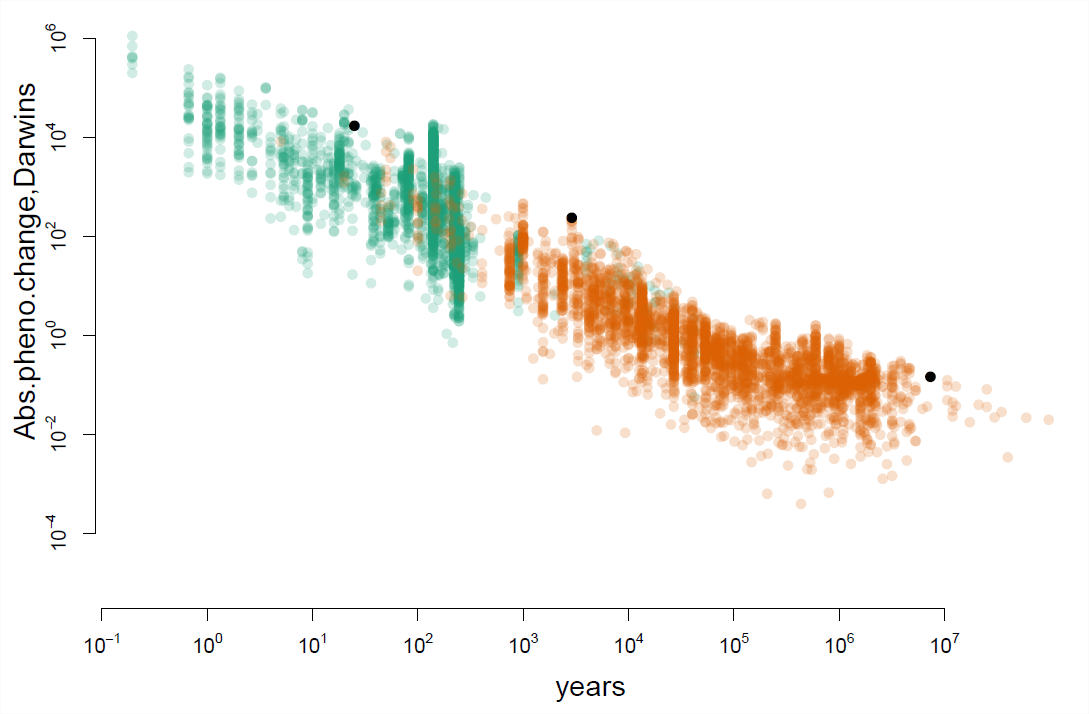
Sin embargo, cuando observamos la evolución fenotípica durante periodos de tiempo más largos suele ser mucho más lenta. Por ejemplo, el punto negro más a la derecha en la Figura\ ref {fig:uyeda_gingerich} muestra la evolución fenotípica a lo largo del linaje que conduce a Triceratops. Triceratops mide en una impresionante longitud de 25.9—29.5 pies. Evolucionaron a partir de un pariente cercano de Protoceratops, que era un poco más grande que una oveja a\(\sim\) 5.9 pies en aproximadamente 7.5 millones de años. Sin embargo, eso es solo un cambio fenotípico de\(0.143\) Darwins, es solo un cambio de aproximadamente cuatro veces en millones de años. Estas tasas de cambio en los dinosaurios no tienen nada en nuestros perros, o muchos otros ejemplos de evolución en escalas de tiempo cortas. Así, los cambios evolutivos que podemos observar en escalas de tiempo cortas explican fácilmente los cambios a largo plazo en los fenotipos cuantitativos.
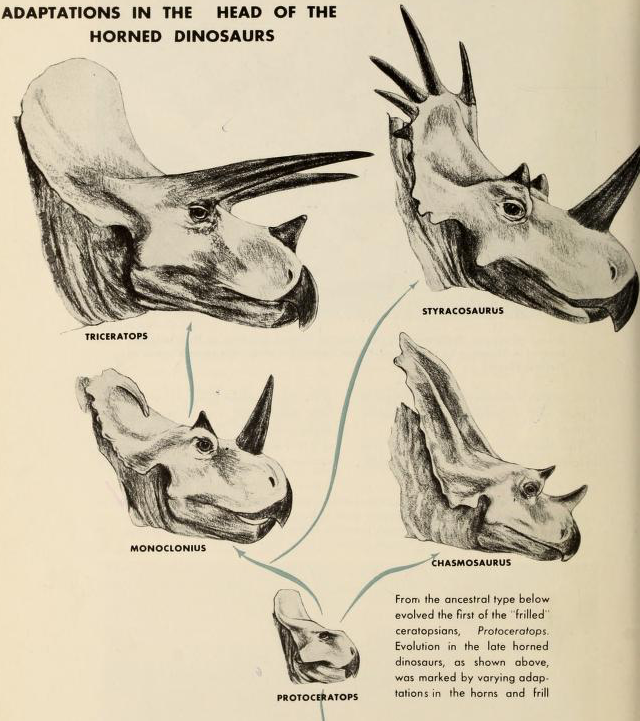
para una divertida y actualizada vista de la filogenia {\ it Coronosauria}. Vea estos
\ href {https://www.geol.umd.edu/~tholtz/G10...04margino.html de Holtz para una filogenia actualizada\ & más completa. \ IANC {El libro de dinosaurios: los reptiles gobernantes y sus parientes. (1951) Colbert, E.H. https://www.biodiversitylibrary.org/.../1up}{American Museo de Historia Natural Biblioteca
La aptitud física y la ecuación del obtentor.
Por lo tanto, la evolución direccional ocurre cuando la selección impulsa un cambio en el fenotipo medio dentro de una generación. Pero precisamente, ¿cómo se relaciona esto con el requisito de selección natural de que los organismos varíen en su aptitud? Algunas formas diferentes de formular la ecuación del Obtentor nos dan una idea de las condiciones para la selección direccional y la relación con los paisajes de fitness.
Selección direccional como covarianza entre aptitud y fenotipo.
Para pensar más detenidamente sobre este cambio dentro de una generación, pensemos en un modelo sencillo de acondicionamiento físico donde nuestro fenotipo afecte la viabilidad de nuestros organismos (es decir, la probabilidad de que sobrevivan para reproducirse). La probabilidad de que un individuo tenga un fenotipo\(X\) antes de la selección es\(p(X=x)\), de manera que el fenotipo medio antes de la selección es
\[\mu_{BS} = \E[X] = \int_{-\infty}^{\infty} x p(x) dx\]
La probabilidad de que un organismo con un fenotipo\(X\) sobreviva para reproducirse es\(w(X)\), y pensaremos en esto como la aptitud de nuestro organismo. La distribución de probabilidad de fenotipos en quienes sobreviven para reproducirse es
\[\mathbb{P}(X | \textrm{survive}) = \frac{p(x) w(x)}{ \int_{-\infty}^{\infty} p(x) w(x) dx}.\]
donde el denominador es una constante de normalización que asegura que nuestra distribución fenotípica se integre a uno. El denominador también tiene la interpretación de ser la aptitud media de la población, a la que llamaremos\(\overline{w}\), i.e.
\[\overline{w} = \int_{-\infty}^{\infty} p(x) w(x) dx. \label{eqn:pheno_mean_fitness}\]
Por lo tanto, podemos escribir el fenotipo medio en quienes sobreviven para reproducirse como
\[\mu_S = \frac{1}{\overline{w}}\int_{-\infty}^{\infty} x p(x) w(x) dx\]
Si nos referimos a centrar la distribución de fenotipos en nuestra población, es decir, establecer el fenotipo antes de la selección a cero, entonces
\[S=\mu_S= \frac{1}{\overline{w}}\int_{-\infty}^{\infty} x p(x) w(x) dx = \frac{1}{\overline{w}}\E \left (X w(X) \right)\]
donde la parte final se deriva del hecho de que la integral está tomando la media de\(X w(X)\) sobre la población.
Como nuestro fenotipo es medio centrado (\(\mathbb{E}(X)=0\)), podemos ver que\(S\) tiene la forma de una covarianza entre nuestro fenotipo\(X\) y nuestra aptitud relativa\(\frac{w(X)}{\overline{w}}\).
\[S = \E \left (X \frac{w(X)}{\overline{w}} \right) =Cov \left(X, \frac{w(X)}{\overline{w}} \right) \label{S_covar}\]
Así, nuestro cambio en el fenotipo medio es directamente una medida de la covarianza de nuestro fenotipo y nuestra aptitud. Reescribiendo la ecuación de nuestro obtentor usando esta observación que vemos
\[R = \frac{V_A}{V_P} Cov \left(X, \frac{w(X)}{\overline{w}} \right)\]
vemos que la respuesta a la selección se debe a que nuestra aptitud (viabilidad) de nuestros organismos/padres varía con nuestro fenotipo, y que el fenotipo de nuestro hijo varía con el fenotipo de nuestros padres.
Gradientes de aptitud y regresiones lineales
Para entender esto con más detalle, imaginemos que calculamos la regresión lineal del fenotipo centrado en\(i\) la media de un individuo (\(X_i\)) sobre la aptitud (\(W_i\)), i.e.
\[W_i \sim \beta X_i + \overline{w} \label{fitness_regression}\]
la pendiente de mejor ajuste de esta regresión (\(\beta\)), la llamaremos el 'gradiente de fitness', viene dada por
\[\beta = Cov(X, \frac{w(X)}{\overline{w}} )/ V_P \label{beta_covar}\]
es decir, el gradiente de aptitud es la covarianza fenotipo-aptitud dividida por la varianza fenotípica. Usando este resultado podemos reescribir la ecuación del obtentor como
\[R= V_A \beta \label{eqn:R_beta}\]
es decir, veremos una respuesta direccional a la selección si existe una relación lineal del fenotipo sobre la aptitud, y si hay varianza genética aditiva para el fenotipo. Como ejemplo de un gradiente de condición física, en la Figura\ ref {fig:red_deer_fitness_grad} el éxito reproductivo de por vida (LRS) del macho Ciervo Rojo se traza contra el peso de sus astas. La línea roja da la regresión lineal de la aptitud (LRS) sobre la masa de asta y la pendiente de esta línea es el gradiente de aptitud (\(\beta\)).

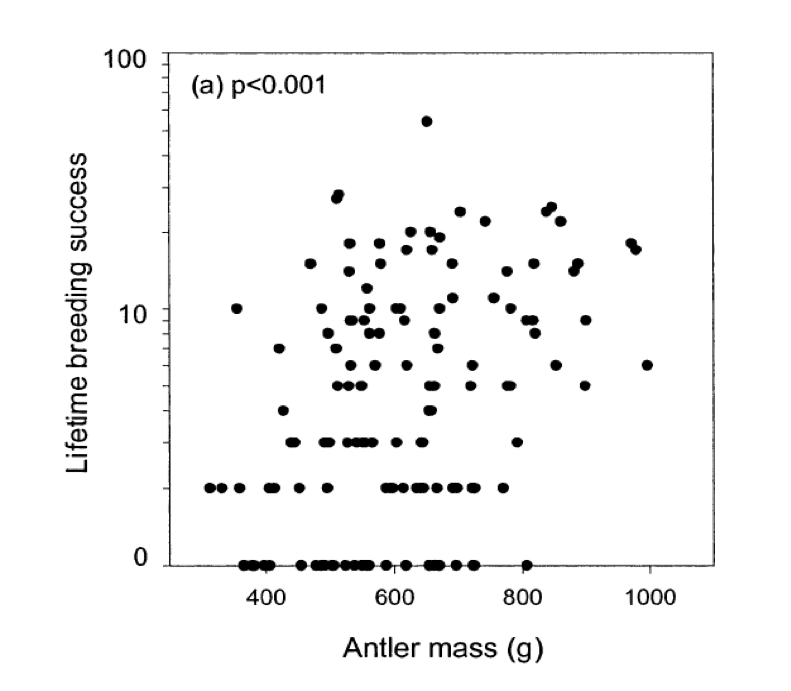
ver el artículo para discutir las complejidades de equiparar este gradiente de selección con la respuesta evolutiva. \ gitcode {https://github.com/cooplab/popgen-no...n_grad_deer.R}.
Teorema fundamental de Fisher de la selección natural
Por último, ¿cómo evoluciona la aptitud media de nuestra población? Si elegimos aptitud relativa para ser nuestro fenotipo (\(X=\frac{w(X)}{\overline{w}}\)), entonces la respuesta en fitness es
\[\begin{aligned} R &= \frac{V_A}{V_P} Cov \left(\frac{w(X)}{\overline{w}} , \frac{w(X)}{\overline{w}} \right) = \frac{V_A}{V_P} V_P \nonumber\\ &=V_A\end{aligned}\]
es decir, la respuesta a la selección es igual a la varianza genética aditiva para la aptitud relativa. O como lo puso Fisher
“La tasa de incremento en la aptitud de cualquier organismo en cualquier momento es igual a su varianza genética en la aptitud en ese momento.” - (pg 37)
Fisher llamó a esto 'el teorema fundamental de la selección natural'. Nuestra prueba aquí es solo un boceto, y se necesitan enfoques más formales para mostrarlo en generalidad. Ha habido mucho crujir de dientes sobre exactamente qué tan amplio tiene este resultado, y exactamente lo que Fisher quiso decir.
Selección Direccional en Paisajes de Fitness

Una metáfora común cuando hablamos de evolución es la de una población explorando un paisaje adaptativo con selección natural empujando a una población hacia estados de mayor aptitud correspondientes a picos en este paisaje (ver por ejemplo Figura\ ref {fig:Fitness_Landscape_1D}). encontró una formulación evocadora del La ecuación del criador que ayuda a nuestra intuición de los paisajes fenotípicos de la aptitud física mostró que, si el fenotipo se distribuye normalmente, la respuesta a la selección (\(R\)) podría escribirse en términos del gradiente (derivado) de la aptitud media (\(\overline{w}\)) de la población como función del fenotipo medio:
\[R = \frac{V_A}{\overline{w}} \frac{\partial \overline{w}}{\partial \bar{x}} \label{eqn:pheno_fitness_landscape} %V_A % \frac{\partial \log \left(\overline{w} \right)}{\partial \bar{z}}\]
¿Qué significa esto? Bueno siempre\(\frac{V_A}{\overline{w}}\) es positivo, por lo que la dirección que nuestra población responde a la selección se predice por el signo de la derivada (ver Apéndice Sección\ ref {sección:cálculo} para más información sobre derivados). Si aumentar ligeramente el fenotipo medio de la población aumentaría la aptitud media (\(\frac{\partial \overline{w}}{\partial \bar{x}} >0\)) nuestra población responderá a esa generación evolucionando hacia valores más altos del rasgo (\(R>0\)), panel izquierdo de la Figura\ ref {fig:Fitness_Landscape_1D_W_WBAR}. Por el contrario, si disminuir ligeramente el fenotipo medio poblacional aumentaría la aptitud media (\(\frac{\partial \overline{w}}{\partial \bar{x}} <0\)) la población evolucionará hacia valores más bajos del fenotipo (panel medio de la Figura\ ref {fig:Fitness_Landscape_1D_W_WBAR}). Así, si las presiones de selección permanecen constantes, podemos pensar que la población evoluciona en un paisaje adaptativo donde la elevación viene dada por la condición media poblacional. La selección natural opera sobre la base de la condición física a nivel individual, pero como resultado de esto nuestra población está aumentando en su condición física promedio, es decir, nuestra población se está adaptando mejor. Discutiremos las advertencias de esta interpretación de la escalada a continuación.

¿Qué sucede cuando llega a la cima de un pico? Bueno en lo alto de un pico\(\frac{\partial \overline{w}}{\partial \bar{x}}=0\), ya que es un máximo local, y así\(R=0\). Suponiendo que la relación entre fitness y fenotipo se mantenga constante, nuestra población se mantendrá en la cima del pico de fitness. Esta visión de la selección natural no implica que la población esté evolucionando al mejor estado posible. Nuestra población apenas está marchando por la colina de la condición física media (figura del panel final\ ref {fig:fitness_landscape_1d_w_w_wbar}). Sin embargo, este pico no es necesariamente el pico de fitness más alto, sino simplemente el pico más cercano. Así que nuestra población puede quedar atrapada en un pico local, pero no global de aptitud física (ver, por ejemplo Figura\ ref {fig:fitness_landscape_1d}).

Un ejemplo dramático que documenta la evolución adaptativa a un nuevo óptimo de condición física es ofrecido por una notable serie temporal de evolución stickleback de un lecho de lago fósil en Nevada. En este lago se depositan cada año las capas de sedimento permitiendo una serie temporal muy detallada con más de cinco mil fósiles medidos. La serie temporal documenta la evolución hacia un nuevo conjunto de fenotipos óptimos en los quince mil años posteriores a la invasión inicial del lago por una especie de dorso fuertemente blindado. En la Figura\ ref {fig:stickleback_fossil_traj} la población media del número de pterigióforos conmovedores, los huesos que sostienen las espinas dorsales, a través del registro fósil (Figura\ ref {fig:stickleback_fossil}). Observe la rapidez con la que la especie evoluciona hacia su nuevo valor, presumiblemente un óptimo de aptitud en su nuevo ambiente, y el largo intervalo de tiempo posterior sobre el cual el fenotipo medio poblacional fluctúa sobre su nuevo valor.
ajustaron a estos datos de series temporales un modelo de población adaptándose a un paisaje de fitness, con un solo pico. Su superficie ajustada se muestra en el panel inferior de la Figura\ ref {fig:stickleback_fossil_traj}. Las flechas muestran los movimientos que el fenotipo medio poblacional está realizando sobre esta superficie de fitness inferida. La población inicialmente da grandes escalones hacia el pico de esta superficie y posteriormente fluctúa alrededor del pico. Bajo la interpretación de que existe un solo pico estacionario estas fluctuaciones representan una deriva genética que golpea aleatoriamente a la población de su óptimo, actuando la selección para restaurar a la población hacia este óptimo local.

Problemas con la interpretación de paisajes de fitness.
En la práctica, los paisajes de fitness pueden no ser constantes. El ambiente puede estar cambiando constantemente por lo que nuestra población se ve constantemente obligada a cambiar para mantenerse al día con el pico de fitness. De hecho, nuestro entorno puede cambiar tan rápido que nuestra población no puede mantenerse al día con el pico. Nuestra población sigue tratando de aumentar su condición media, de 'adaptarse', pero el paisaje en sí está evolucionando. En el caso de cambios ambientales muy rápidos, nuestra población puede deslizarse cada vez más lejos del pico, y como consecuencia su condición media disminuye lo que puede llevar a la población a la extinción si nuestra población cae\(\overline{w}<1\) por debajo por el tiempo suficiente. Las condiciones de extinción son un área activa de investigación en el campo del 'rescate evolucionario'. De manera más general, para que nuestro resultado de paisaje de fitness (eqn\ ref {eqn:feno_fitness_landscape}) se mantenga, y para que podamos hablar de nuestra población que intenta evolucionar a estados de aptitud media más altos, necesitamos que la aptitud de nuestros fenotipos sea independiente de la frecuencia de otros fenotipos en la población. (Esta independencia permite suponer que la aptitud de los individuos no es una función del fenotipo medio, como se necesita en eqn\ ref {eqn:proof_landscape}). El supuesto de independencia de frecuencia puede no sostenerse cuando hay competencia entre individuos, por ejemplo, por recursos o compañeros, ya que entonces la aptitud de un individuo depende de las estrategias perseguidas por otros individuos en las poblaciones.
Selección estabilizadora y disruptiva
Hasta ahora acabamos de observar la selección direccional, donde la selección actúa para cambiar el fenotipo medio. Sin embargo, también podemos usar modelos genéticos cuantitativos para describir otros modos de selección, extendiendo desde los efectos sobre la media poblacional, el siguiente paso natural es pensar en la selección que actúa sobre la varianza poblacional. La selección podría actuar más fuertemente contra individuos en las colas de la distribución, con aquellos más cercanos al fenotipo medio teniendo mayor aptitud, lo que disminuye la varianza. La selección también podría desfavorecer a los individuos cercanos a la media poblacional, con individuos con fenotipos extremos teniendo mayor aptitud, lo que actúa para aumentar la varianza de la población.
La selección direccional ocurre por la covarianza entre nuestro fenotipo y aptitud, eqn\ ref {s_CoVar}. Así como expresar la selección direccional como una covarianza nos permitió caracterizar la selección direccional como la relación lineal entre la aptitud y el fenotipo\(\beta\), podemos resumir la varianza reduciendo la selección al incluir un término cuadrático en la regresión de la aptitud sobre el fenotipo
\[w_i \sim \beta x_i + \frac{1}{2} \gamma x_i^2 + \overline{w} \label{fitness_regression_stab}\]
Este\(\gamma\), el coeficiente del término cuadrático en nuestro modelo, es el gradiente de selección cuadrático: la covarianza de aptitud y la desviación cuadrada de la media fenotípica (\(\mu_{BS}\)), i.e.
\[\gamma = \frac{Cov\left(w(X), (X-\mu_{BS})^2 \right)}{V^2}\]
Nuestro\(\gamma\) describe la curvatura de la superficie de fitness alrededor de la media. Los valores de\(\gamma<0\) son consistentes con la estabilización de la selección, reduciendo la varianza. Mientras que los valores de\(\gamma>0\) son consistentes con la selección disruptiva, aumentando la varianza.

Bajo selección estabilizadora los individuos con fenotipos extremos en cualquiera de las colas tienen menor aptitud, el resultado de lo cual es reducir la varianza fenotípica dentro de una generación. Un caso clásico de selección estabilizadora es el peso al nacer en humanos. Mary Karn recopiló datos de casi catorce mil embarazos de 1935-46 por peso al nacer y mortalidad. Estos datos son retrazados en la Figura\ ref {fig:birth_weight}. La varianza de todos los nacimientos es\(1.575\) lb\(^2\), mientras que en los nacidos vivos esta se redujo a\(1.26\) lb\(^2\), una reducción de 20% en la varianza debido a la estabilización de la selección. Cabe señalar que esta presión de selección se ha reducido considerablemente a lo largo de las décadas en sociedades con acceso a una buena atención prenatal.

En África Central, los semilleros de vientre negro (Pyrenestes ostrinus) muestran una selección disruptiva en un notable polimorfismo del tamaño del pico (Figura\ ref {Black_bellied_seedcrackers_beaks}). Los individuos de pico pequeño se alimentan de semillas blandas de una especie de escocia de pantano, mientras que los individuos de pico grande se alimentan de semillas duras de otra cornisa, lo que requiere diez veces la fuerza para romper. Registraron el destino de cientos de juveniles, y encontraron que los individuos con tamaños de pico intermedio sobrevivieron mucho tasas más bajas (Figura\ ref {black_bellied_seedcrackers_beaks}) porque no estaban bien adaptados a ninguno de los recursos semilla. La longitud de ruptura está sujeta a selección disruptiva, como también puede verse por el término cuadrático negativo significativo en la regresión de la probabilidad de supervivencia en la longitud de ruptura. La varianza de longitud de mandíbula en la muestra total de individuos fue\(0.5\) mm\(^2\) en los sobrevivientes esta varianza aumentó en un factor de\(2.5\) a\(1.3\)\(^2\) mm.

Para ilustrar cómo la selección direccional y los términos cuadráticos juegan durante la adaptación, consideremos la mosca de la agalla de vara de oro (Eurosta solidaginis), también conocida como el fabricante de gallos de bola de oro. Ver Figura\ ref {gall_size_stab}. Como su maravilloso nombre lo indica, este insecto pone sus huevos en plantas de vara de oro, y las larvas liberan químicos obligando a la planta a formar una agalla que forma un hogar para las larvas a medida que se desarrollan. Si bien esto parece un trato bastante dulce para las larvas, no está exento de peligros.

Cuando las pequeñas agallas de bola caen presa del parasitismo de avispas parasitoides. Cuando todas las agallas de bola son pequeñas en la selección de población impulsa una fuerte selección direccional positiva en el tamaño de la agalla, con poca selección estabilizadora. Observe en el panel izquierdo de la Figura\ ref {gall_size_stab} el buen acuerdo entre el gradiente de selección lineal y el ajuste incluyendo un término lineal y cuadrático. Sin embargo, agallas más grandes caen bajo la capa de depredación de pájaros carpinteros vellosos y garbanzos de cabeza negra, quienes buscan las sabrosas larvas. Así, se favorecen las agallas de tamaño intermedio, un pico de condición física que la población alcanza rápidamente. Una vez en este pico, como se muestra en el panel derecho de la Figura\ ref {gall_size_stab} no hay selección direccional, es decir, no hay pendiente lineal, pero hay una fuerte selección estabilizadora, es decir, un término cuadrático. De esta manera, la población se mantendrá en este pico de fitness indefinidamente si el ambiente permanece inalterado.

La selección natural fenotípica requiere variación en los fenotipos impacta la aptitud de manera no aleatoria. Para que ocurra la evolución por selección natural necesitamos que esta variación fenotípica sea heredable.
Un modelo simple para la respuesta a la selección direccional en un fenotipo viene dado por la ecuación del obtentor. La respuesta esperada a la selección entre generaciones adyacentes (\(R\)) es proporcional a la respuesta a la selección dentro de una generación, el diferencial de selección (\(S\)), donde la constante de proporcionalidad es la heredabilidad de sentido estrecho (\(h^2\)) del rasgo. Por lo tanto, esperamos ver, y de hecho vemos, respuestas fuertes a la selección cuando la selección provoca grandes cambios dentro de una generación en fenotipos heredables.
Si las presiones de selección y la heredabilidad permanecen constantes, esperamos una respuesta lineal a la selección a través de muchas generaciones. A menudo podemos ver esto en experimentos de selección, pero en la naturaleza las presiones de selección a menudo fluctúan de generación en generación. Los grandes cambios en el fenotipo que vemos en el registro fósil se explican fácilmente por las fortalezas de selección que vemos actuar en escalas de tiempo cortas.
Hay otras dos formas comunes de escribir la ecuación del obtentor. El primero utiliza el gradiente de selección (\(\beta\)), la regresión de la aptitud sobre el fenotipo. El segundo, la interpretación del paisaje de fitness se basa en escribir este gradiente de selección como la derivada de la aptitud media por fenotipo. La forma del paisaje de fitness a la ecuación del obtentor nos ayuda a entender cómo y cuándo podemos esperar que la selección actúe para aumentar la aptitud media de la población.
Podemos entender otras formas de selección en nuestro fenotipo que se espera que actúen sobre la varianza fenotípica en lugar de la media, como la selección disruptiva y estabilizadora, por extensiones de la ecuación del obtentor para incluir términos para gradientes de selección cuadrática.
Estás estudiando la rápida evolución del tamaño de los órganos de luz en luciérnagas (Photinus pyralis) en respuesta a la contaminación lumínica en una pradera en Ohio. En enero de 1985, se construyó una carretera a través de la pradera con alumbrado alumbrado público. Dado que las luciérnagas utilizan señales de luz para localizar compañeros, los individuos con órganos de luz más pequeños y por lo tanto menos visibles tuvieron menos éxito en el apareamiento en estas nuevas condiciones de luz. Sabes que el órgano de luz tenía, en promedio, 4mm de largo antes de la construcción de la autopista. En 2005, el tamaño promedio de órganos ligeros en esta población antes del apareamiento era de 6mm. Si esta luciérnaga tiene 1 generación por año y la heredabilidad de sentido estrecho es 0.1, ¿cuál fue la longitud media de los órganos ligeros de los individuos que se reproducían con éxito en 1985 (el primer año de selección)?
Eres un criador de conejos, y decides que quieres conejos con pelaje largo. La varianza fenotípica es\(4\textrm{cm}^2\). La covarianza de la longitud del pelaje entre los hermanos completos es\(1\textrm{cm}^2\). La longitud media del pelaje en la población inicial es\(3\textrm{cm}\). Tú eliges criar la parte superior\(\frac{1}{3}\) de la población con el pelaje más largo, y su longitud media de pelaje es\(5\) cm.
Suponiendo que la covarianza entre hermanos se debe únicamente a la varianza genética aditiva, ¿cuántas generaciones de este régimen de selección tardarán para que la longitud del pelaje esté\(10cm\) en la población?


