4.10: Ejercicio- Filtrado Paso Alto
- Última actualización
- Guardar como PDF
- Page ID
- 151840
Hasta este punto, nos hemos centrado en los filtros paso bajo, pero en este ejercicio veremos cómo funciona el filtrado paso alto. La única diferencia fundamental es que las funciones de respuesta al impulso son diferentes.
Con parámetros típicos (por ejemplo, una frecuencia de corte de media amplitud de 0.1 Hz), el filtrado paso alto requiere una función de respuesta de impulso muy larga, por lo que no funciona muy bien con datos EEG o ERP de época (a menos que las épocas tengan una duración de muchos segundos). Por lo general, aplicará filtrado paso alto al EEG continuo (como en algunos de los ejercicios de capítulos anteriores). Sin embargo, es un poco más fácil crear formas de onda simuladas y visualizarlas con ERPs, por lo que aplicaremos filtros de paso alto a los datos ERP simulados en este ejercicio. Como compromiso, creé formas de onda simuladas con una época más larga de lo habitual (de -1000 a +1000 ms). Pero con datos reales, querría épocas aún más largas (o, mejor aún, aplicar filtros de paso alto a los datos EEG continuos).
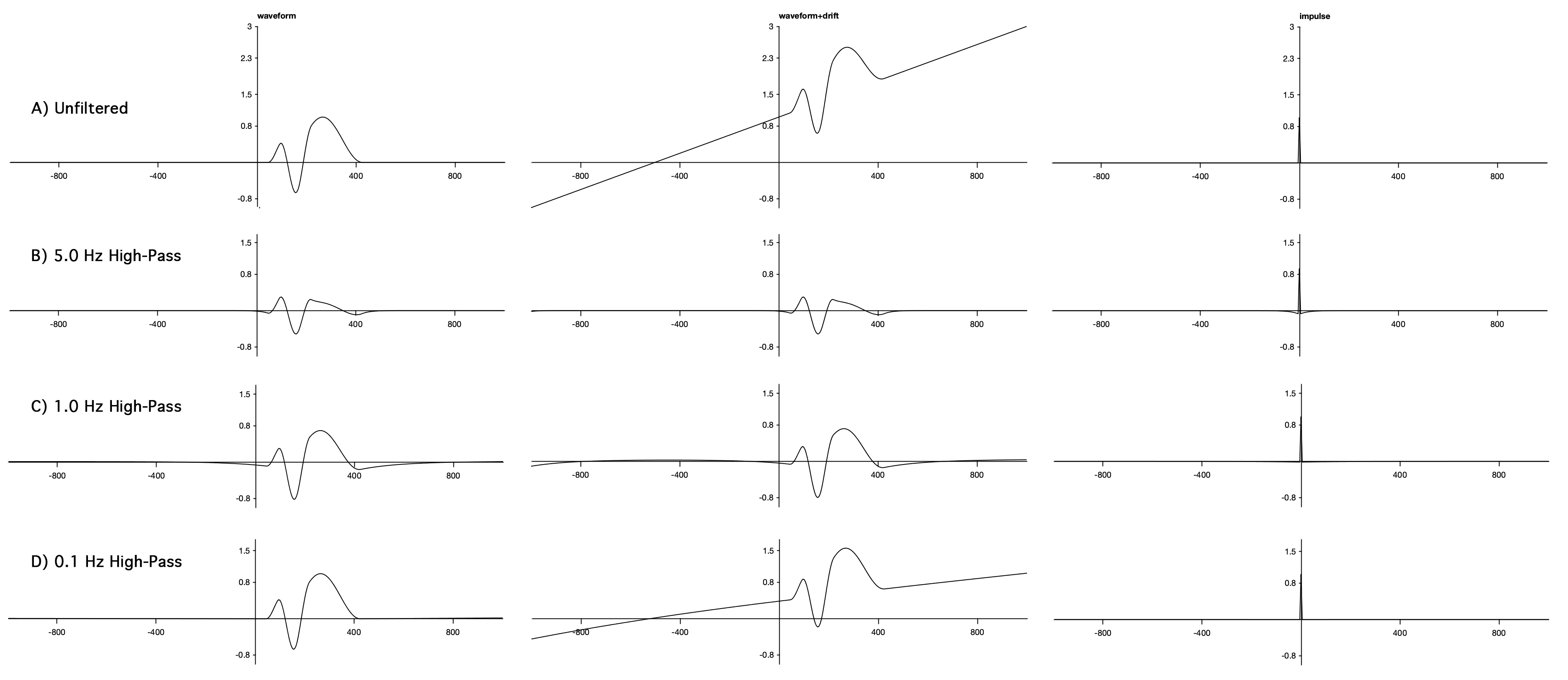
Para comenzar, salga y reinicie EEGLAB y luego cargue el ERPSet en el archivo llamado waveform+drift. erp. Si trazas los ERPs, verás algo como Captura de Pantalla 4.11A. El canal 1 es la misma forma de onda artificial que hemos usado antes, pero con una época más larga. El canal 2 es la misma forma de onda, pero con una deriva lineal superpuesta sobre él. El canal 3 es un impulso que podemos usar para visualizar las funciones de respuesta al impulso de los filtros que usaremos.
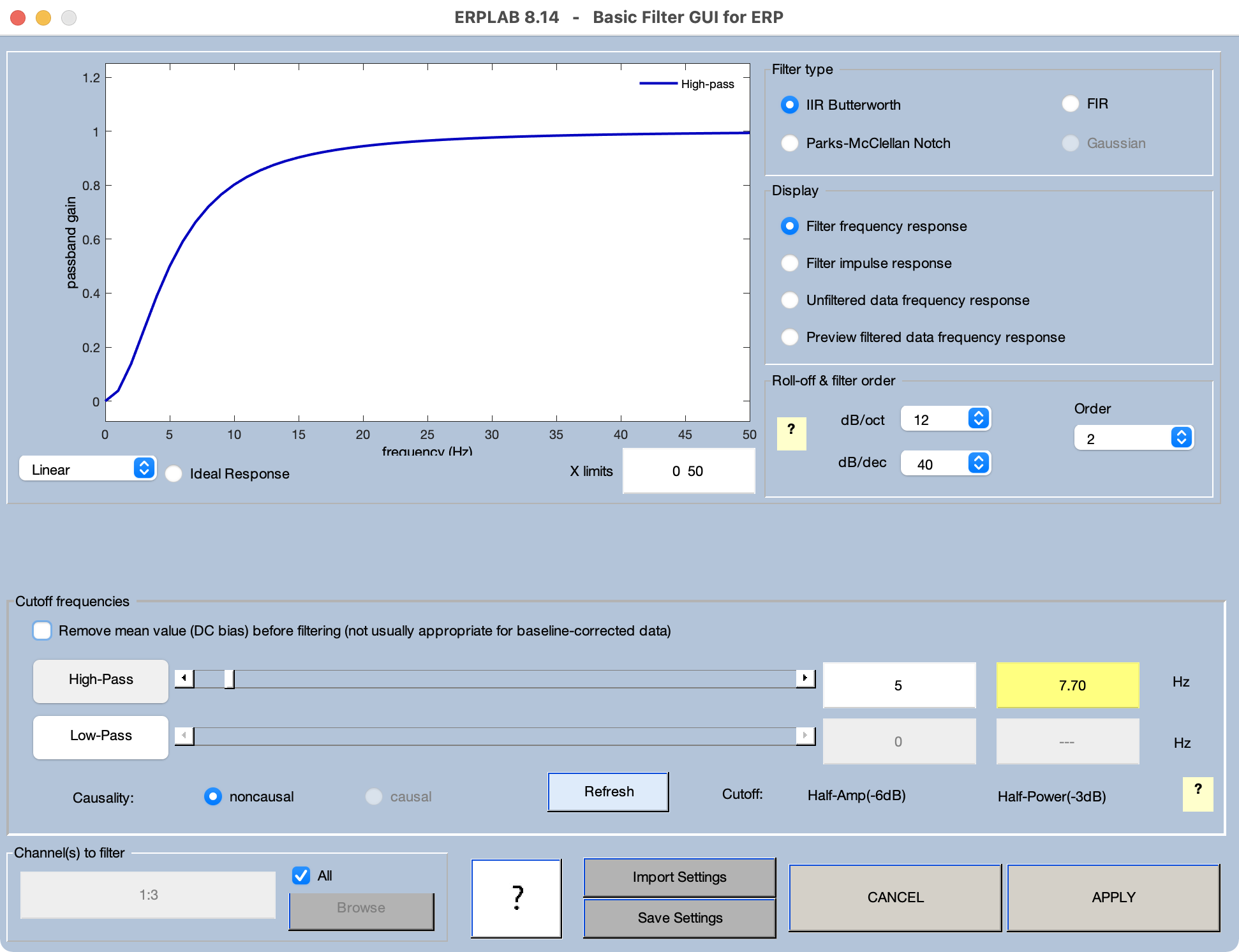
Vamos a comenzar usando un corte de filtro de paso alto de 5 Hz, lo que significa que estamos filtrando frecuencias por debajo de 5 Hz. Nunca recomendaría usar este corte con datos reales (excepto algunos casos especiales, como la investigación sobre la respuesta auditiva del tronco encefálico). Sin embargo, esto hará que sea más fácil ver cómo se ve la función de respuesta al impulso y cómo impacta la forma de onda filtrada.
Inicie la herramienta de filtrado y establezca los parámetros como se muestra en la Captura de Pantalla 4.12. En particular, apague el filtro de paso bajo, encienda el filtro de paso alto, establezca el corte de paso alto en 5 Hz y ajuste el roll-off a 12 dB/octava. Y asegúrate de que Canal (s) a filtrar esté configurado en Todos. Si miras la función de respuesta de frecuencia que se muestra en la parte superior izquierda, verás que la ganancia está cerca de cero para las frecuencias más bajas, alcanza 0.5 a 5 Hz (porque esa es la frecuencia de corte de media amplitud) y luego comienza a acercarse a la asíntota de 1.0 por aproximadamente 10 Hz.
Ahora mira la función de respuesta al impulso cambiando la configuración de Pantalla de Respuesta de frecuencia de filtro a Respuesta de impulso de filtro. Debería verse como Captura de pantalla 4.13. Es muy diferente de la función de respuesta al impulso de un filtro de paso bajo. Los filtros paso bajo y paso alto tienen efectos opuestos (eliminando frecuencias altas versus bajas), por lo que tienen funciones de respuesta al impulso en gran parte opuestas. Mientras que las funciones de respuesta al impulso de paso bajo que hemos visto tenían valores positivos cerca del tiempo cero, esta función de respuesta al impulso de paso alto es negativa cerca del tiempo cero (pero está cerca de 1.0 justo en el tiempo cero). Las razones de esto se discuten en los Capítulos 7 y 12 de Suerte (2014). Aquí, solo tendrás que tomar mi palabra para ello.
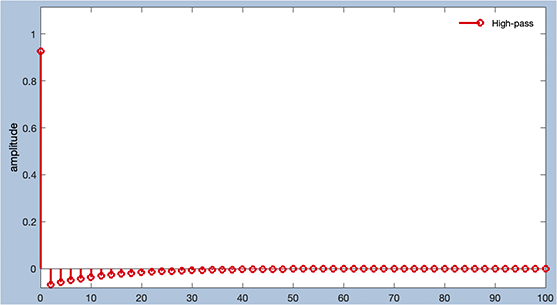
Continúe y haga clic en APLICAR para ejecutar el filtro y luego trazar las formas de onda filtradas. Deberías ver algo como Captura de Pantalla 4.11B. Primero mira el impulso (Canal 3), que ahora muestra la función de respuesta al impulso del filtro. Se pueden ver los valores negativos que rodean el tiempo cero, pero son bastante pequeños. Esto se debe a que la función de respuesta de impulso para un filtro de paso alto debe sumar a cero. Si la respuesta al impulso se extiende por un largo periodo de tiempo, los valores individuales deben ser muy pequeños.
Ahora mira la forma de onda+canal de deriva (Canal 2). La buena noticia es que el filtro prácticamente ha eliminado la deriva. La mala noticia es que el filtro ha producido picos negativos artifácticos al principio y al final de la forma de onda. También se pueden ver estos picos artifácticos en el canal sin la deriva (Canal 1). El filtro también ha reducido la amplitud y cambia la forma de la forma de onda ERP, pero eso es de esperar porque gran parte de la potencia en la forma de onda cae en las frecuencias que son atenuadas por el filtro (lo que puede confirmar haciendo activo el ERPSet sin filtrar y usando EEGLAB > ERPLAB > Herramientas de filtro y frecuencia > Trazar espectro de amplitud para datos ERP). Estas distorsiones son la razón por la que nunca recomendaría usar un filtro como este con datos reales (a excepción de las respuestas auditivas del tronco encefálico, que se limitan en gran medida a frecuencias más altas).
Si piensas en la función de respuesta al impulso, puedes entender por qué el filtro produce picos negativos artificiales al principio y al final de la forma de onda. La forma de onda sin filtrar comienza y termina con valores positivos. Cuando reemplazamos estos valores con la función de respuesta al impulso, los valores negativos a la izquierda y derecha del punto actual en la función de respuesta al impulso producen valores negativos antes y después de los picos positivos. Tenga en cuenta que si la forma de onda contenía picos negativos, los picos artifácticos serían positivos (porque un voltaje negativo de la forma de onda sin filtrar multiplicado por un valor negativo en la función de respuesta al impulso crea un valor positivo).
A continuación vamos a probar un filtro que no es tan extremo, pero que aún tiene una frecuencia de corte más alta de la que recomendaría, es decir, 1 Hz. Vuelva a activar el ErpSet original con forma de onda y deriva en el menú ERPSets, inicie la herramienta de filtrado y cambie el corte de 5 Hz a 1 Hz. Observe la función de respuesta al impulso en la herramienta de filtrado. Se puede ver un gran valor positivo en el tiempo cero, pero los valores cercanos apenas son negativos. La función se extiende por un periodo de tiempo más largo que la función para el filtro de 5 Hz, y cada punto individual debe estar más cerca de cero para que los puntos sumen a cero.
Continúe y haga clic en APLICAR y luego graficar los datos filtrados. Debería verse como Captura de pantalla 4.11C. La deriva en el Canal 2 todavía se ha ido en gran parte, pero no hemos atenuado tanto la forma de onda ERP, así que eso es una mejora. Sin embargo, los picos negativos artefactuales al principio y al final de la forma de onda todavía están presentes. Por eso no recomendaría usar un corte de 1 Hz.
Ahora probemos el corte de filtro paso alto que normalmente recomiendo para la mayoría de los estudios de ERP perceptuales, cognitivos y afectivos, es decir, 0.1 Hz. Vuelva a activar el ERPSet sin filtrar, inicie la herramienta de filtrado y cambie el corte a 0.1 Hz. Si miras la función de respuesta al impulso en la herramienta de filtrado, realmente no puedes ver mucho más allá del valor positivo en el tiempo cero. Eso significa que el filtro será muy suave. Aplica el filtro y mira las formas de onda. Como se muestra en la Captura de Pantalla 4.11D, el filtro solo ha reducido parcialmente la deriva en el Canal 2. Sin embargo, no ha producido ninguna distorsión notable de la forma de onda ERP. Es decir, el filtro no ha atenuado la forma de onda, y no ha producido ningún pico artefacto.
Este conjunto de ejemplos ilustra un principio importante: Puede atenuar completamente las derivas lentas en sus datos pero distorsionar sus formas de onda ERP, o puede no atenuar completamente el ruido de baja frecuencia y evitar distorsionar sus formas de onda ERP. No se pueden atenuar completamente las derivas y evitar distorsionar la forma de onda. Esto se debe a la relación inversa entre los dominios de tiempo y frecuencia: Cuanto más restrinja las frecuencias con un filtrado extenso, más distorsiona el curso temporal de la forma de onda ERP.
Tenga en cuenta que las derivas lentas son deflexiones de ruido que surgen principalmente de la piel, y son positivas en algunas pruebas y negativas en otras. Agregan ruido aleatorio a tus datos, disminuyendo tu poder para encontrar efectos estadísticamente significativos. Obviamente eso no es algo bueno. Sin embargo, es mucho peor usar un filtro que induzca efectos artifácticos que son estadísticamente significativos pero completamente falsos, lo que hace que saque conclusiones incorrectas. Es por eso que generalmente recomiendo un corte de paso alto de 0.1 Hz: reduce razonablemente bien el ruido de baja frecuencia, pero generalmente no produce artefactos sustanciales.
En la primera edición de mi libro de texto ERP (Luck, 2005), recomendé usar 0.01 Hz como corte de media amplitud. En los años siguientes, sin embargo, mis colaboradores y yo comparamos sistemáticamente una variedad de diferentes puntos de corte, y normalmente encontramos que 0.1 Hz producía la mejor reducción de ruido sin ninguna distorsión sustancial de las formas de onda (Kappenman & Luck, 2010; Tanner et al., 2015). Si estás viendo ERPs muy lentas (como la actividad de retardo contralateral), 0.01 o 0.05 podría ser mejor que 0.1, pero en la mayoría de los casos encuentro que 0.1 Hz funciona mejor.


