6.9: Ejercicio - Comparación de ensayos correctos y de error
- Última actualización
- Guardar como PDF
- Page ID
- 151327
En este ejercicio, vamos a crear bins para las pruebas de error así como para las pruebas correctas. Esto nos permitirá observar la negatividad relacionada con errores (ERN, también llamada N e), una respuesta ERP negativa sobre sitios de electrodos frontocentrales que se produce cuando el participante comete un error obvio (ver la excelente revisión de Gehring et al., 2012). Los errores son bastante comunes en los ensayos raros en el paradigma de bichos raros porque la respuesta para la categoría Frecuente se vuelve altamente cebada. Cuando estás haciendo la tarea, te encuentras presionando el botón Frecuente aunque te des cuenta (un momento demasiado tarde) de que deberías estar presionando el botón Raro.
Aunque el primer informe publicado de la ERN utilizó una tarea rara (Falkenstein et al., 1990), esta tarea es menos que ideal para observar errores porque los ensayos de error son un pequeño subconjunto de una categoría de estímulo ya rara, lo que lleva a muy pocos ensayos de error. En el ERP CORE, en cambio, usamos una tarea de flankers para mirar el ERN, y ni siquiera analizamos las pruebas de error en la tarea de bichos raros. En este ejercicio, vamos a analizar las pruebas de error en la tarea de bichos raros y buscar la ERN. ¿Crees que veremos una ERN? ¡No estaba seguro de que lo veríamos hasta que analicé los ensayos de error por primera vez ayer!
Mi primer paso fue crear un nuevo archivo descriptor de bin que incluya bins para las pruebas de error. El archivo se llama BDF_P3_Accuracy.txt —continúe y ábralo en el editor de texto de Matlab (haciendo doble clic en él en el panel Carpeta actual). Verás que acabo de agregar bins para los estímulos raros y frecuentes seguidos de una respuesta de error (código de evento 202) en lugar de ser seguido por una respuesta correcta (código de evento 201).
Si EEGLAB se está ejecutando, salga de él y reinícielo para que todo esté fresco, y luego vuelva a cargar el conjunto de datos original (12_P3_Corrected_elist.set). Luego ejecute BINLISTER, usando BDF_P3_ Accuracy.txt como el archivo descriptor bin. Puede usar cualquier nombre de conjunto de datos que sea conveniente, pero asegúrese de guardar EventList como un nuevo archivo de texto.
Echa un vistazo al nuevo archivo de texto EventList. Cerca de la parte superior, debajo de la información del encabezado, verás el número de pruebas en cada bin. Como antes, hubo 30 ensayos Raros seguidos de una respuesta correcta y 153 Ensayos frecuentes seguidos de una respuesta correcta en los Contenedores 1 y 2. Sin embargo, solo hubo 9 Ensayos raros seguidos de una respuesta incorrecta y un mísero 3 Ensayos frecuentes seguidos de una respuesta incorrecta. Y esto es en realidad más pruebas de error de lo que era típico (probablemente porque los tiempos de respuesta de este participante fueron más rápidos que los de la mayoría de los participantes en este experimento). En el experimento ERP CORE flankers, que fue diseñado para observar la ERN, controlamos el número de errores diciéndoles a los participantes que aceleraran si cometían errores en menos del 10% de los ensayos y diciéndoles que redujeran la velocidad si cometieron errores en más del 20% de los ensayos. Pero el experimento raro no fue diseñado para mirar al ERN, así que no intentamos controlar el número de errores. Algunos participantes hicieron mucho, y algunos apenas hicieron ninguno.
Como de costumbre, el siguiente paso es epoch los datos (EEGLAB > ERPLAB > Extraer épocas basadas en bines). Es posible que la rutina de época todavía tenga los ajustes del promedio de respuesta bloqueada que hicimos en el ejercicio anterior, pero ahora vamos a hacer promedios bloqueados por estímulos, así que asegúrese de que el rango de tiempo de época esté establecido en -200 800 y el período de corrección de línea base esté establecido en Pre. Haga clic en Ejecutar y asigne el nombre al conjunto de datos resultante como desee. Ahora promedia los datos. Debe nombrar el ERPSet 12_P3_Accuracy resultante y guardarlo como un archivo llamado 12_P3_Accuracy.ERP. Lo necesitarás para un ejercicio posterior.
La rutina de promediado imprime los mejores, peores y valores medios de ASMe en la ventana de comandos. Siempre debes mirar estos valores para asegurarte de que no haya ningún problema con la calidad de los datos. Verás que el valor máximo es mucho mayor que la mediana, lo que te indica que podría haber un bin o canal problemático. Por supuesto, podríamos esperar una baja calidad de datos para los ensayos de error dada la poca presencia de ensayos. Consistente con esto, el valor máximo fue para la bin con Estímulos frecuentes seguido de una respuesta incorrecta, la cual solo tuvo 3 ensayos.
Eche un vistazo a todos los valores de ASMe usando EEGLAB > ERPLAB > Opciones de calidad de datos > Mostrar medidas de calidad de datos en una tabla. Para las pruebas correctas (Bins 1 y 2), los valores se ven bastante razonables. El SME cuantifica el error estándar de medición, y un error estándar de entre 1 y 3 µV es razonablemente pequeño en relación con la amplitud >15 µV de la P3b. Ahora mira los valores de estímulos raros seguidos de una respuesta incorrecta (Bin 3). La mayoría de los valores siguen siendo menores a 5 µV, lo que parece razonable dado el pequeño número de ensayos. Si miras los valores para el Bin 4, sin embargo, verás muchos valores que un poco más grandes. Esto tiene sentido dado que solo tuvimos 3 juicios en esta papelera.
¿Cuántos ensayos necesitas? Algunos investigadores han intentado dar una respuesta simple a esta pregunta, pero no existe una respuesta simple porque depende del número de participantes (Baker et al., 2020) y la magnitud del efecto que se está estudiando (ver Boudewyn et al., 2018).
Ahora vamos a trazar los ERPs (usando EEGLAB > ERPLAB > Plot ERP > Trazar formas de onda ERP; es posible que deba hacer clic en el botón RESET para borrar los parámetros de trazado que usamos en el ejercicio anterior). Comenzaremos trazando las pruebas Raras correctas e incorrectas, así que especifica los Bins 1 y 3. Ahora por fin podemos responder a la pregunta de si los errores producen una ERN en este experimento (al menos para este participante). El lado izquierdo de Screenshot 6.5 muestra lo que deberías ver en el canal FCz, donde el ERN suele ser más grande. Se puede ver que el voltaje es más negativo desde ~200-400 ms en las pruebas de error que en las pruebas correctas. ¡Esta es la ERN! La replicación es una piedra angular de la ciencia, y seguro que es agradable ver que este efecto se puede replicar.
Se puede ver que el voltaje es más positivo para ensayos de error que para ensayos correctos desde ~400-600 ms. Este efecto también se ha visto en muchos estudios previos, y se llama el error positividad o P e.
Captura de pantalla 6.5
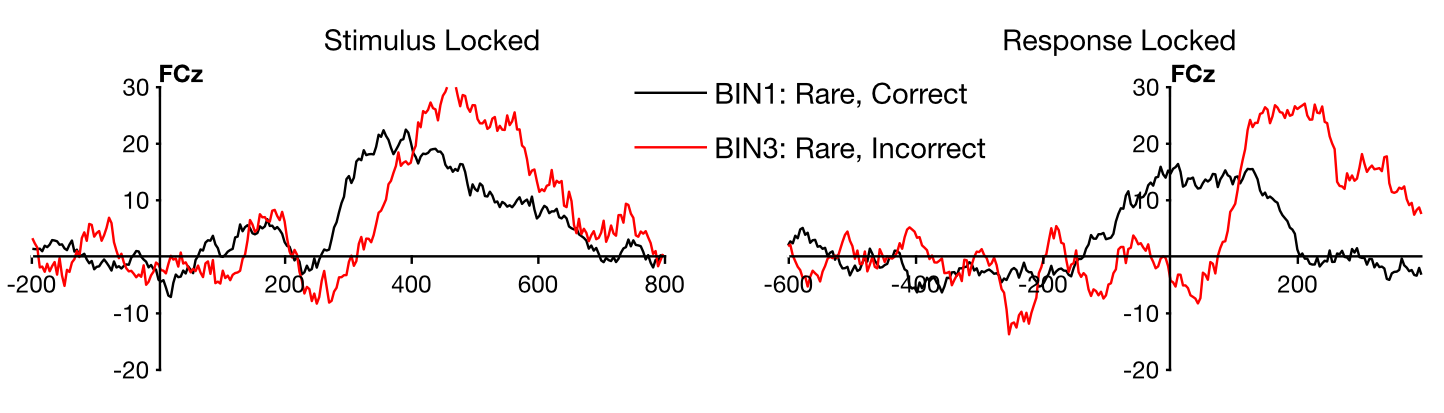
Como siempre, querrás mirar todos los canales para ver la distribución del efecto en el cuero cabelludo. Se puede ver que la diferencia entre los ensayos de error y los ensayos correctos (tanto en las ventanas de tiempo ERN como Pe) es mayor en los sitios de electrodos frontal y central de la línea media. Esto es lo que normalmente se observa cuando se utilizan como referencia las mastoides o sitios cercanos. Si te interesa, puedes intentar volver a hacer referencia al promedio de todos los sitios y ver cómo esto cambia la distribución del cuero cabelludo.
También debe intentar trazar las formas de onda frecuentes correctas e incorrectas (Bins 2 y 4). Sin embargo, es difícil ver mucho porque solo hubo 3 ensayos frecuentes incorrectos, por lo que las formas de onda son extremadamente ruidosas.
La ERN suele ocurrir justo alrededor del momento de la respuesta. Cuando los RTs varían mucho de un ensayo a otro, la ERN en los promedios bloqueados por estímulos ocurre en diferentes momentos en diferentes ensayos, y esto hace que la ERN parezca “manchada” en promedios bloqueados por estímulos. Las formas de onda también parecen como si el P3b estuviera simplemente desplazado hacia la derecha en las pruebas de error. De hecho, cuando Bill Gehring vio por primera vez el ERN, estaba mirando promedios bloqueados por estímulos, y no estaba seguro de que fuera un componente real. No obstante, cuando hizo promedios de respuesta bloqueada, el ERN era una desviación grande y hermosa en el tiempo cero. Se puede leer la historia de cómo descubrió la ERN en el Capítulo 3 de la Suerte (2014).
El participante que hemos estado viendo en este capítulo no tenía mucha variabilidad RT, por lo que la ERN es fácilmente visible en los promedios bloqueados por estímulos. Pero hagamos promedios de respuesta bloqueada para ver si esto hace que la ERN sea aún más clara. Para ello, siga las instrucciones del ejercicio anterior para hacer un promedio de respuesta bloqueada (especialmente usando una época de -600 a 400 ms), pero use BDF_P3_Accuracy_Response_Locked.txt como archivo descriptor bin.
Para el canal FCz, las formas de onda bloqueadas por respuesta deberían verse como las del lado derecho de la Captura de Pantalla 6.5. Ahora la ERN aparece como una deflexión negativa relativamente aguda, alcanzando su punto máximo poco después del tiempo cero (el tiempo de la pulsación del botón). Se puede ver que es una desviación distinta en lugar de simplemente ser un desplazamiento hacia la derecha en el P3b.


