6.1.3: Elipses no Centradas en el Origen

Última actualización
Guardar como PDF

Page ID: 108779

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Elipses Centradas en (h, k)

Tu tarea es dibujar la elipse\(\ 16(x-2)^{2}+4(y+3)^{2}=144\). ¿Cuál es el vértice de tu gráfica y dónde se ubicarán los focos de la elipse?

Elipses Centradas en (h, k)

Una elipse no siempre tiene que ser colocada con su centro en el origen. Si el centro es toda\(\ (h, k)\) la elipse se desplazarán\(\ h\) unidades hacia la izquierda o derecha y k unidades hacia arriba o hacia abajo. La ecuación se convierte\(\ \frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\). Abordaremos cómo cambian los vértices, co-vértices y focos en el siguiente problema.

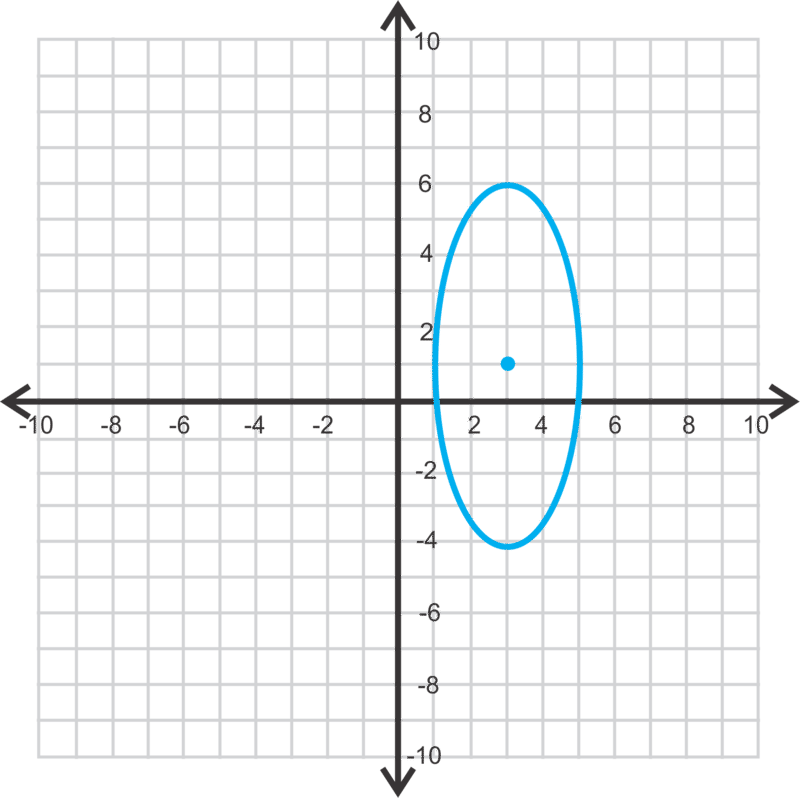
Vamos a graficar\(\ \frac{(x-3)^{2}}{16}+\frac{(y+1)^{2}}{4}=1\). Luego, encontraremos los vértices, co-vértices y focos.

Primero, sabemos que se trata de una elipse horizontal porque\(\ 16>4\). Por lo tanto, el centro es\(\ (3,-1)\) y\(\ a=4\) y\(\ b=2\). Usa esta información para graficar la elipse.

Para graficar, trazar el centro y luego salir 4 unidades a la derecha y a la izquierda y luego arriba y abajo dos unidades. Así es también como puedes encontrar los vértices y co-vértices. Los vértices son (3 ± 4, −1) o (7, −1) y (−1, −1). Los co-vértices son (3, −1 ± 2) o (3, 1) y (3, −3).

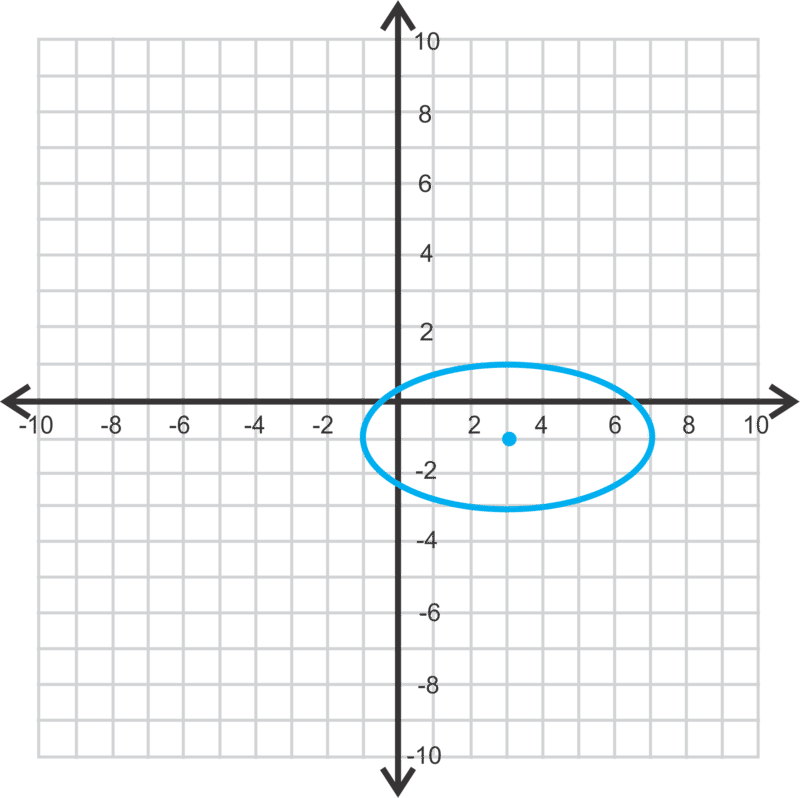
f-d_d9af0957c67bb6e0338c3f50c9bd7fc02b79dfc4cf846920ca92a85e+image_tiny+image_tiny.png

Para encontrar los focos, necesitamos encontrar el\(\ c\) uso\(\ c^{2}=a^{2}-b^{2}\).

\ (\\ comenzar {alineado}
c^ {2} &=16-4=12\\
c &=2\ sqrt {3}
\ end {alineado}\)

Por lo tanto, los focos son\(\ (3 \pm 2 \sqrt{3},-1)\).

A partir de este problema, podemos crear fórmulas para encontrar los vértices, co-vértices y focos de una elipse con centro\(\ (h, k)\). Además, al graficar una elipse, no centrada en el origen, asegúrate de trazar el centro.

Orientación	Ecuación	Vértices	Co-vértices	Focos
Horizontal	\(\ \frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\)	\(\ (h±a, k)\)	\(\ (h, k±b)\)	\(\ (h±c, k)\)
Vertical	\(\ \frac{(x-h)^{2}}{b^{2}}+\frac{(y-k)^{2}}{a^{2}}=1\)	\(\ (h, k±a)\)	\(\ (h±b, k)\)	\(\ (h, k±c)\)

Ahora, vamos a encontrar la ecuación de la elipse con vértices (−3, 2) y (7, 2) y co-vértice (2, −1).

Estos dos vértices crean un eje mayor horizontal, haciendo que la elipse sea horizontal. Si no estás seguro, traza la información dada en un conjunto de ejes. Para encontrar el centro, usa la fórmula de punto medio con los vértices.

\(\ \left(\frac{-3+7}{2}, \frac{2+2}{2}\right)=\left(\frac{4}{2}, \frac{4}{2}\right)=(2,2)\)

La distancia de uno de los vértices al centro es\(\ a,|7-2|=5\). La distancia desde el covértice hasta el centro es\(\ b,|-1-2|=3\). Por lo tanto, la ecuación es\(\ \frac{(x-2)^{2}}{5^{2}}+\frac{(y-2)^{2}}{3^{2}}=1\) o\(\ \frac{(x-2)^{2}}{25}+\frac{(y-2)^{2}}{9}=1\).

Por último, graficemos\(\ 49(x-5)^{2}+25(y+2)^{2}=1225\) y encontremos los focos.

Primero tenemos que conseguir esto en forma estándar, como las ecuaciones anteriores. Para hacer el lado derecho 1, necesitamos dividir todo por 1225.

\ (\\ begin {array} {c}
\ frac {49 (x-5) ^ {2}} {1225} +\ frac {25 (y+2) ^ {2}} {1225} =\ frac {1225} {1225}\
\ frac {(x-5) ^ {2}} {25} +\ frac {(y+2) ^ {2}} {49} =1
\ end {array}\)

Ahora, sabemos que la elipse será vertical porque 25 < 49. a=7, b=5 y el centro es (5, −2).

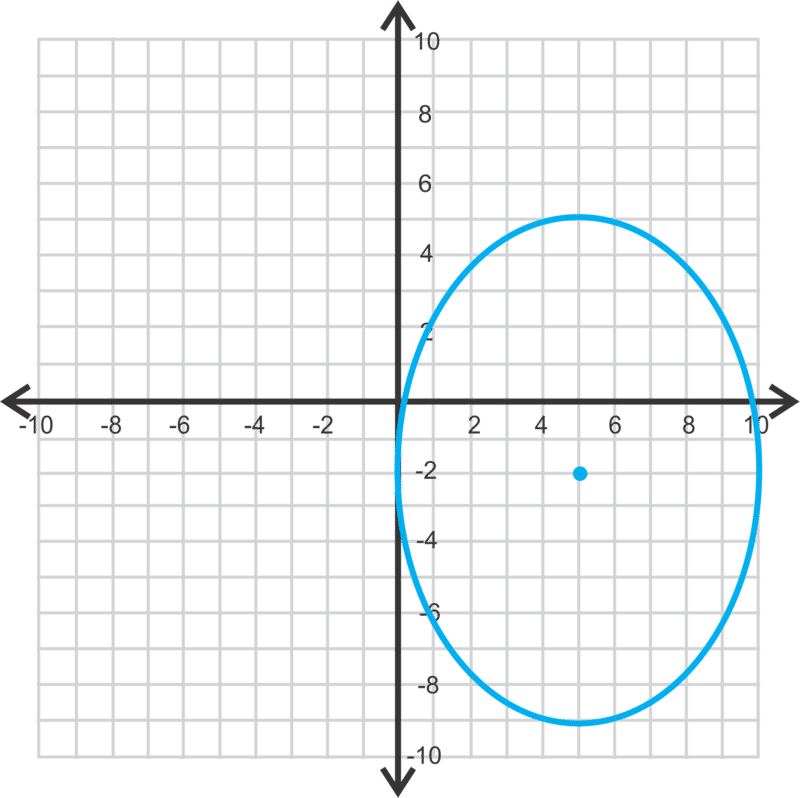
f-d_55c0f3ed918f8b1f580abfdcd62e59e26d71e0a9b88f869aae0f46e9+image_tiny+image_tiny.png

Para encontrar los focos, primero necesitamos encontrar\(\ c\) usando\(\ c^{2}=a^{2}-b^{2}\).

\ (\\ begin {array} {c}
c^ {2} &=49-25=24\\
c&=\ sqrt {24} =2\ sqrt {6}
\ end {array}\)

Los focos son\(\ (5,-2 \pm 2 \sqrt{6})\) o\(\ (5,-6.9)\) y\(\ (5,2.9)\).

Ejemplos

Ejemplo 1

Anteriormente, se le pidió encontrar el vértice de su gráfica y determinar dónde se ubicarán los focos de la elipse.

Solución

Primero necesitamos obtener nuestra ecuación en forma de\(\ \frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\). Entonces dividimos ambos lados por 144.

\ (\\ begin {array} {r}
\ frac {16 (x-2) ^ {2}} {144} +\ frac {4 (y+3) ^ {2}} {144} =\ frac {144} {144}\
\ frac {(x-2) ^ {2}} {9} +\ frac {(y+3) ^ {2}} {36}
\ final {matriz}\)

Ahora podemos ver eso\(\ h=2\) y\(\ 3=-k\) o\(\ k=-3\). Por lo tanto el origen es\(\ (2,-3)\).

Porque\(\ 9<36\), sabemos que se trata de una elipse vertical. Para encontrar los focos, use\(\ c^{2}=a^{2}-b^{2}\).

\ (\\ comenzar {alineado}
c^ {2} &=36-9=27\\
c &=\ sqrt {27} =3\ sqrt {3}
\ end {alineado}\)

Los focos son por lo tanto\(\ (2,-3+3 \sqrt{3})\) y\(\ (2,-3-3 \sqrt{3})\)

Ejemplo 2

Encuentra el centro, vértices, co-vértices y focos de\(\ \frac{(x+4)^{2}}{81}+\frac{(y-7)^{2}}{16}=1\).

Solución

El centro es\(\ (-4,7), a=\sqrt{81}=9\) y\(\ b=\sqrt{16}=4\), haciendo la elipse horizontal. Los vértices son\(\ (-4 \pm 9,7)\) o\(\ (-13,7)\) y\(\ (5,7)\). Los co-vértices son\(\ (-4,7 \pm 4)\) o\(\ (−4,3)\) y\(\ (-4,11)\). \(\ c^{2}=a^{2}-b^{2}\)Úselo para encontrar\(\ c\).

\ (\\ begin {array} {l}
c^ {2} &=81-16=65\\
c&=\ sqrt {65}
\ end {array}\)

Los focos son\(\ (-4-\sqrt{65}, 7)\) y\(\ (-4+\sqrt{65}, 7)\).

Ejemplo 3

Grafica\(\ 25(x-3)^{2}+4(y-1)^{2}=100\) y encuentra los focos.

Solución

Cambia esta ecuación a forma estándar para poder graficar.

\ (\\ begin {array} {l}
\ frac {25 (x-3) ^ {2}} {100} +\ frac {4 (y-1) ^ {2}} {100} =\ frac {100} {100}\
\ frac {(x-3) ^ {2}} {4} +\ frac {(y-1) ^ {2}} {25} =1
\ final {matriz}\)

centro:\(\ (3,1), b=2, a=5\)

Encuentra los focos.

\ (\\ comenzar {alineado}
c^ {2} &=25-4=21\\
c &=\ sqrt {21}
\ end {alineado}\)

Los focos son\(\ (3,1+\sqrt{21})\) y\(\ (3,1-\sqrt{21})\).

Ejemplo 4

Encuentra la ecuación de la elipse con co-vértices (−3, −6) y (5, −6) y enfoque (1, −2).

Solución

Los co-vértices (−3, −6) y (5, −6) son los extremos del eje menor. Tiene |−3−5|=8 unidades de largo, haciendo b=4. El punto medio entre los co-vértices es el centro.

\(\ \left(\frac{-3+5}{2},-6\right)=\left(\frac{2}{2},-6\right)=(1,-6)\)

El foco es (1, −2) y la distancia entre éste y el centro es de 4 unidades, o\(\ c\). Encuentra\(\ a\).

\ (\\ begin {array} {l}
16=a^ {2} -16\\
32=a^ {2}\\
a=\ sqrt {32} =4\ sqrt {2}
\ end {array}\)

La ecuación de la elipse es\(\ \frac{(x-1)^{2}}{16}+\frac{(y+6)^{2}}{32}=1\).

Revisar

Encuentra el centro, vértices, co-vértices y focos de cada elipse debajo.

\(\ \frac{(x+5)^{2}}{25}+\frac{(y+1)^{2}}{36}=1\)
\(\ (x+2)^{2}+16(y-6)^{2}=16\)
\(\ \frac{(x-2)^{2}}{9}+\frac{(y-3)^{2}}{49}=1\)
\(\ 25 x^{2}+64(y-6)^{2}=1600\)
\(\ (x-8)^{2}+\frac{(y-4)^{2}}{9}=1\)
\(\ 81(x+4)^{2}+4(y+5)^{2}=324\)
Grafica la elipse en #1.
Grafica la elipse en #2.
Grafica la elipse en #4.
Grafica la elipse en #5.

Usando la siguiente información, encuentra la ecuación de cada elipse.

vértices: (−2, −3) y (8, −3) covértices: (3, −5)
vértices: (5, 6) y (5, −12) enfoque: (5, −7)
co-vértices: (0, 4) y (14, 4) foco: (7, 1)
focos: (−11, −4) y (1, −4) vértice: (−12, −4)
Extensión Reescribe la ecuación de la elipse, 36x ² + 25y ² − 72x + 200y − 464 = 0 en forma estándar, completando el cuadrado tanto para los términos x como para y.

Respuestas para problemas de revisión

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 10.6.

Atribuciones de imagen

[Figura 1]
Crédito: Ad Meskens
Fuente: https://commons.wikimedia.org/wiki/File:Illu_pancrease.jpg; https://commons.wikimedia.org/wiki/File:President%27s_Park_with_White_House.jpg