Inicio
Educación Básica
Cálculo
3: Límites - Continuidad
3.2: Continuidad en un Punto, Prueba de Continuidad, Tipos de Discontinuidad

3.2: Continuidad en un Punto, Prueba de Continuidad, Tipos de Discontinuidad

Última actualización
Guardar como PDF

Page ID: 105985

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

En el concepto anterior, la continuidad de una función se presentaba intuitivamente a través de la imaginería de usar un lápiz para dibujar una gráfica sobre una hoja de papel (sobre un cierto intervalo del dominio) y nunca levantar el lápiz del papel. Mientras no se levante el lápiz del papel, se puede considerar que el gráfico es continuo durante ese intervalo de dibujo. Esta ciertamente no es una descripción rigurosa de la continuidad, pero dada esta analogía, qué expectativas podría tener sobre las operaciones aritméticas en dos funciones que son continuas en un intervalo común; o la existencia de mínimos y máximos de una función continua; o la existencia de valores intermedios entre dos valores de función?

Propiedades de las funciones continuas

El concepto anterior identificó las características de una función que es continua en un punto, y a lo largo de un intervalo. Vamos a explorar Dadas dos funciones f (x) y g (x) que son continuas a lo largo de un intervalo cerrado [a, b], ¿esperaría que las operaciones aritméticas en estas dos funciones también producirían funciones continuas sobre [a, b]?

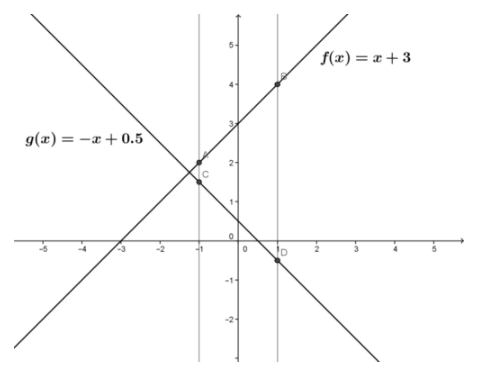
Dadas las funciones f (x) =x+3 y g (x) =−x+0.5 en el intervalo cerrado [−1,1], determinar si f (x) y g (x) son continuas en el intervalo.

Las funciones f (x) y g (x) se muestran en la gráfica. La inspección de cada gráfica de función y su ecuación, muestra que cada una de ellas se define sobre el intervalo cerrado y el límite de función en cada punto del intervalo es igual al valor de la función en el punto. Ambas funciones son continuas en el intervalo.

Screen Shot 2020-09-22 a las 8.45.53 PM.png

Fundación CK-12 - CC BY-NC-SA

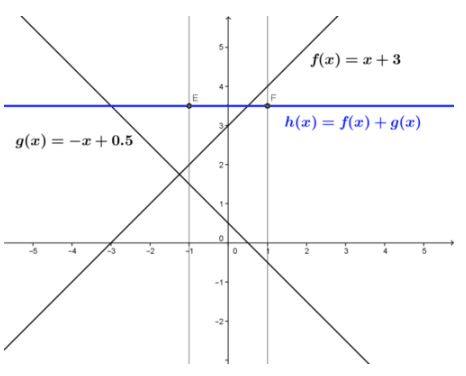
Usando las mismas funciones e intervalo anteriores, determine si h (x) =f (x) +g (x) es continuo en el intervalo.

La suma de las dos funciones viene dada por h (x) =3.5, y se muestra en la figura. La función sum, una constante, se define sobre el intervalo cerrado y el límite de función en cada punto del intervalo es igual al valor de función constante en cada punto. La función sum es continua en el intervalo.

Screen Shot 2020-09-22 a las 8.46.24 PM.png

Fundación CK-12 - CC BY-NC-SA

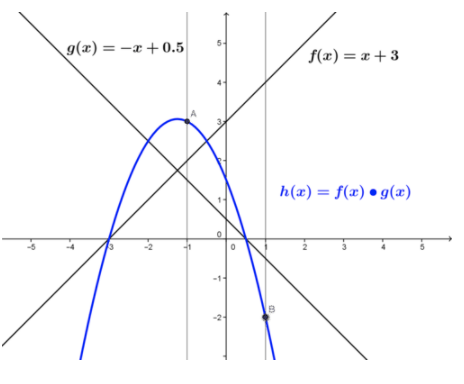
Aún usando el intervalo y las funciones anteriores, determinar si h (x) =f (x) g (x) es continuo en el intervalo.

El producto de las dos funciones viene dado por h (x) = (x+3) (−x+0.5) =−x ² +2.5x−1.5, y se muestra en la figura. La función producto, una parábola, se define sobre el intervalo cerrado y el límite de función en cada punto del intervalo es igual al valor de la función del producto en cada punto. La función del producto es continua en el intervalo.

Screen Shot 2020-09-22 a las 8.47.34 PM.png

Fundación CK-12 - CC BY-NC-SA

¿Y el cociente de dos funciones continuas?

Dadas las funciones f (x) =x+3 y g (x) =−x+0.5 en el intervalo cerrado [−1,1], determinar si ^{f (x)}/_{g (x)} es continuo en el intervalo.

El cociente de las dos funciones viene dado por

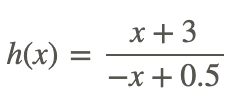
Screen Shot 2020-09-22 a las 8.48.54 PM.png

y se muestra en la figura.

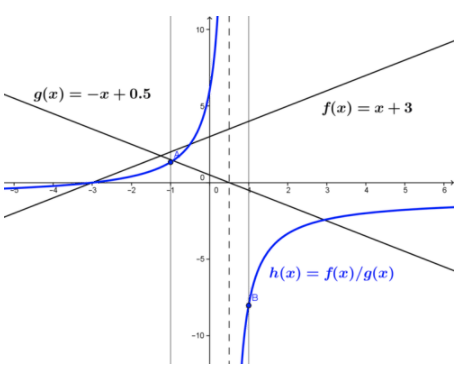
Screen Shot 2020-09-22 a las 8.49.22 PM.png

Fundación CK-12 - CC BY-NC-SA

En el intervalo cerrado [−1,1], x=0.5 es el único lugar donde la función h (x) no está definida, y

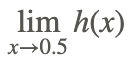
Screen Shot 2020-09-22 a las 9.05.21 PM.png

r en el intervalo cerrado.

Los hallazgos en las funciones simples anteriores pueden generalizarse en las siguientes propiedades.

Si f (x) y g (x) son continuos en cualquier valor real c sobre el intervalo cerrado [a, b], entonces los siguientes también son continuos en cualquier valor real c sobre el intervalo cerrado [a, b]:

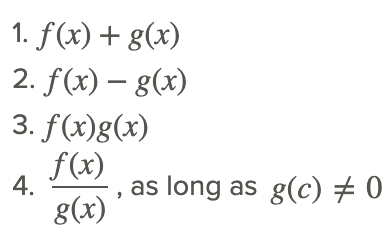
Screen Shot 2020-09-22 at 9.33.57 PM.png

El Teorema del Valor Intermedio y el Teorema del Valor Extremo (Min-Max) son otras dos propiedades de una función que es continua a lo largo de un intervalo cerrado.

El teorema del valor intermedio y el teorema del valor extremo

El Teorema del Valor Intermedio establece que si una función es continua en un intervalo cerrado [a, b], entonces la función asume cada valor entre f (a) y f (b).

El Teorema del Valor Intermedio puede ser utilizado para analizar y aproximar ceros de funciones.

Utilice la Función de Valor Intermedio para mostrar que hay al menos un cero de la función f (x) =3x ⁴ −3x ³ −2x+1 en el intervalo indicado [1,2].

La gráfica de esta función, que se muestra a continuación, tiene una forma algo parecida a una parábola, y es continua en el intervalo.

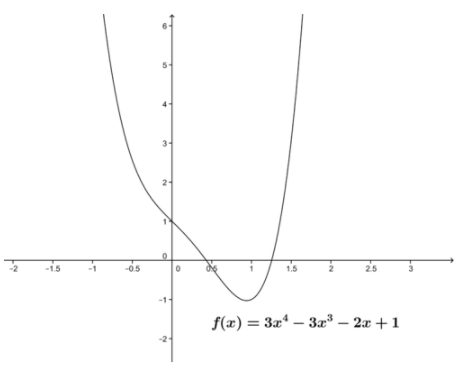
Screen Shot 2020-09-22 at 9.34.40 PM.png

CC BY-NC-SA

Para aplicar el Teorema del Valor Intermedio, necesitamos encontrar un par de valores x que tengan valores de función con diferentes signos. Algunos valores se muestran en la siguiente tabla.

x	1.1	1.2	1.3
*f (x)*	-0.80	-0.36	0.37

Vemos que el signo de los valores de la función cambia de negativo a positivo en algún lugar entre 1.2 y 1.3. De ahí que por el teorema del Valor Intermedio, hay algún valor c en el intervalo (1.2, 1.3) tal que f (c) =0.

El Valor Extremo (Teorema Min-Max) es una consecuencia del Teorema del Valor Intermedio.

El Teorema del Valor Extremo (Min-Max) establece que si una función f (x) es continua en un intervalo cerrado I, entonces f (x) tiene tanto un valor máximo como un valor mínimo en I.

Ejemplos

Ejemplo 1

Anteriormente, se le preguntó acerca de sus expectativas para la continuidad de funciones formadas por operaciones aritméticas en dos funciones continuas. La conclusión de esta sección es que, a excepción del cociente de funciones, las operaciones aritméticas sobre dos funciones que son continuas en un punto o en un intervalo producen una nueva función que es continua en el punto o en el intervalo. Con el cociente de dos funciones, la preocupación es siempre identificar dónde está el denominador 0; en esta ubicación la función del cociente no es continua.

Ejemplo 2

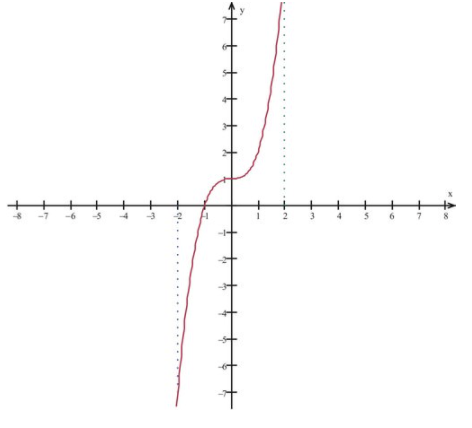
Considera f (x) =x ³ +1 e intervalo I= [−2,2]. Determinar los valores mínimo y máximo.

Dado que la función es continua en el intervalo cerrado I, esta función tiene un mínimo y un máximo en el intervalo. El gráfico de funciones muestra que en x=−2 la función tiene un valor mínimo f (−2) =−7; y en x=2, un valor máximo f (2) =9.

Screen Shot 2020-09-22 a las 9.35.33 PM.png

CC BY-NC-SA

Revisar

Para #1 -5, explica cómo sabes que la función tiene una raíz en el intervalo dado. (Pista: Use la Función de Valor Intermedio para mostrar que hay al menos un cero de la función en el intervalo indicado. ):

f (x) =x ³ +2x ² −x+1, en el intervalo [-3, -2].
f (x) =x ^.5 −x√3−1, en el intervalo [9,10].
f (x) =x2+x−2, en el intervalo [-3,0].
f (x) =4x2−1x2+3x+2, en el intervalo [-1,0].
f (x) =2x+3−4, en el intervalo [-3,0].
Verdadero o Falso: f (x) =sin (x) +cos (x) tiene una raíz en el intervalo [0, π].
Verdadero o Falso: Por el Teorema del Valor Intermedio f (x) =sin (x) +cos2 (x) no tiene raíz en el intervalo [0, π] ya que f (0) =f (π) =1.
Verdadero o Falso: f (x) =x2+1cos (x) tiene una raíz en el intervalo [0, π].
¿En qué intervalo es f (x) =x−sin (x) +1 garantizado por la IVT para tener una raíz?

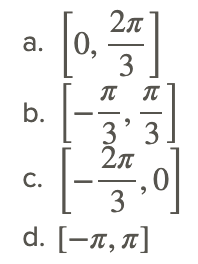
Screen Shot 2020-09-24 at 7.11.54 PM.png

10. Encuentra un intervalo en el que f (x) =e ^x +x tenga una raíz.

11. Encuentra intervalos en los que f (x) =x ³ +5x ² −4x−20 tiene una raíz.

Para #12 -15, use el Teorema del Valor Extremo para determinar si la declaración dada es verdadera o falsa.

El Teorema del Valor Extremo garantiza que la función |sin (x3) | ^0.5 tiene un valor mínimo en el intervalo [-3, 3].
El Teorema del Valor Extremo garantiza que la función (x−1) ³ tiene un valor máximo en el intervalo [1, 3].
El Teorema del Valor Extremo garantiza que la función x ² +3x+2 tiene un valor mínimo en el intervalo [-3, 0].
El Teorema del Valor Extremo garantiza que la función ^4x/_{x ² +3x+2} tiene un valor mínimo en el intervalo [-3, 0].

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 2.10.

vocabulario

Término	Definición
Continuo	La continuidad para un punto existe cuando los límites de los lados izquierdo y derecho coinciden con la función evaluada en ese punto. Para que una función sea continua, la función debe ser continua en cada punto de un dominio ininterrumpido.
Función continua	Una función continua es una función sin roturas ni huecos. Contiene un número infinito e incontable de valores.
discontinuo en un punto	Una función es discontinua en un punto a si la función no está definida en x=a.
Teorema del valor extremo	El teorema del valor extremo establece que en cada intervalo [a, b] donde una función es continua hay al menos un máximo y un mínimo. Es decir, debe tener al menos dos valores extremos.
Teorema del valor intermedio	El teorema del valor intermedio establece que si f (x) es continuo en algún intervalo [a, b] y n está entre f (a) y f (b), entonces hay algo de c∈ [a, b] tal que f (c) =n.
puntos de discontinuidad	Los puntos de discontinuidad para una función son los valores de entrada de la función donde la función es discontinua.

Recursos adicionales

PLIX: Juega, aprende, interactúa, explora - Propiedades de las funciones continuas

Video: La continuidad y el teorema del valor intermedio

Práctica: Continuidad en un Punto, Prueba de Continuidad, Tipos de Discontinuidad

Mundo Real: Nuevas Órbitas