9.4: Funciones de probabilidad y densidad de probabilidad
- Page ID
- 105902
La probabilidad es un concepto que es una parte familiar de nuestras vidas. Usamos la probabilidad como la medida de que algún evento (en un conjunto de eventos posibles) realmente ocurrirá. El conjunto de eventos posibles puede ser finito y, por lo tanto, denominarse una variable aleatoria discreta, o infinita y constituir una variable aleatoria continua. Una probabilidad, P, es un número tal que 0≤P≤1. Cuanto más cerca esté P a 0, más improbable es que ocurra el evento; cuanto más cerca esté P a 1, más probable es que ocurra el evento. Además, la suma de todas las probabilidades que cubren todos los eventos posibles en el conjunto, debe sumarse a 1. ¿Se puede determinar antes de comenzar qué tipo de variable aleatoria (discreta o continua) estaría asociada con probabilidades calculadas usando integrales definidas? ¿Por qué?
Funciones de densidad de probabilidad
En esta sección, veremos cómo calcular el valor de una probabilidad usando una función llamada función de densidad de probabilidad (pdf). Hay muchas formas diferentes de funciones de densidad de probabilidad, y veremos algunas.
Si el servicio postal te dijo que recibirás un paquete que has estado esperando mañana en algún momento, podrías preguntarte: ¿Cuál es la probabilidad de que reciba mi paquete en algún momento entre las 3:00 PM y las 5:00 PM dado que el horario de operaciones del servicio postal es entre las 7:00 AM y las 6:00 PM?
A falta de más información, una forma de encontrar una solución es señalar que dado que la oficina de correos opera por un total de 11 horas (7 AM a 6 PM), y el intervalo de interés es de las 2 horas entre las 3 PM y las 5 PM, la probabilidad de que llegue tu paquete podría ser
\[ P=\frac{2 \mbox{ hours}}{11 \mbox{ hours}}=0.182 \nonumber\]
Por lo que existe una probabilidad de 0.182 de que el servicio postal entregue su paquete en algún momento entre las 3 PM y las 5 PM. Debido a que no había nada especial en el intervalo de 3 pm a 5 pm, la probabilidad de 0.182 podría aplicarse a cualquier intervalo de 2 horas durante el periodo de 11 horas de operación. Esto también significa que existe una probabilidad de 0.818 de que el paquete no se entregue durante ese intervalo (es decir, 1-0.182).
Pero, matemáticamente, ¿cómo se mantiene el cálculo anterior cuando el intervalo de 11 horas y el intervalo de 2 horas contienen un número infinito de veces? ¿Cómo puede un infinito dividido por otro infinito producir una probabilidad de 0.182? (Nota: Los posibles tiempos de entrega en el intervalo de 11 horas representan una variable aleatoria continua.) Para resolver este problema, podemos representar la probabilidad de entrega del paquete en cualquier momento en el intervalo de 11 horas como definido por un rectángulo de altura\( \frac{1}{11} \nonumber\) y longitud 11, con área resultante igual a 1. Al observar el intervalo de 2 horas, podemos ver que es igual al\( \frac{2}{11} \nonumber\) área rectangular total de 1. Por ello es conveniente representar las probabilidades como áreas.
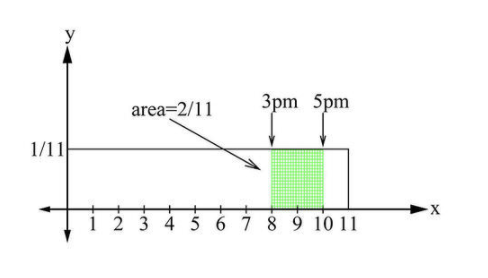
Dado que las áreas pueden definirse por integrales definidas, también podemos definir la probabilidad de que ocurra un evento dentro de un intervalo [a, b] por la integral definida\( P(a≤x≤b)=\int\limits_a^b f(x)dx \nonumber\) donde f (x) se llama la función de densidad de probabilidad (pdf).
Una función f (x) se denomina función de densidad de probabilidad si
- f (x) ≥0 para todos x
- El área debajo de la gráfica de f (x) sobre toda la línea real es exactamente 1
- La probabilidad de que x esté en el intervalo [a, b] es
\[ P(a≤x≤b)=\int\limits_a^b f(x)dx \nonumber\]
es decir, el área bajo la gráfica de f (x) de a a b.
En el problema anterior, la función de densidad de probabilidad f (x) se denomina función de densidad de probabilidad uniforme (plana) (pdf).
Existen muchas otras funciones de densidad de probabilidad que cuando se usan darían una respuesta diferente a la pregunta sobre el tiempo de entrega de nuestro paquete.
Supongamos que después de pensar y discutir con los vecinos, usted decide que sería mejor usar una función de densidad de probabilidad triangular como se muestra a continuación para la entrega de paquetes en su área. ¿Cuál es la probabilidad de que reciba su paquete en algún momento entre las 3:00 PM y las 5:00 PM?
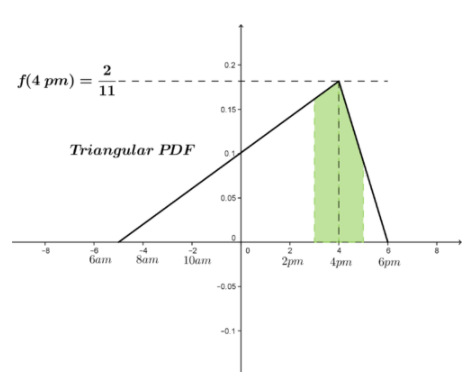
El pdf triangular muestra una variación que se puede modelar como:
\[ f(x)= \begin{cases} \frac{2}{99} (x+12) − \frac{14}{99}, −5 ≤ x ≤ 4 \\ \frac{−1}{11} (x+12)+ \frac{18}{11}, 4≤x≤6 \end{cases} \nonumber\]
Tenga en cuenta que el pdf es 0 fuera del intervalo anterior.
La probabilidad de que el paquete llegue entre las 3 y las 5 pm se puede determinar como
\( P(a≤x≤b)=\int\limits_a^b f(x)dx \nonumber\)
\( P(3≤x≤5)=\int\limits_3^5 f(x)dx \nonumber\)
\( = \int\limits_3^4 (\frac{2}{99} (x+12)− \frac{14}{99})dx+\int\limits_4^5 −\frac{1}{11} (x+12)−\frac{18}{11})dx \nonumber\)
\( =\frac{2}{99}[\frac{x^2}{2}+5x]_3^4−\frac{1}{11}[\frac{x^2}{2}−6x]_4^5 \nonumber\)
\( =\frac{17}{99}+\frac{1.5}{11} \nonumber\)
\( P(3≤x≤5)=\frac{30.5}{99}≈0.308 \nonumber\)
Usando el pdf triangular, la probabilidad de recibir el paquete entre las 3 y las 5 pm ha aumentado a 0.308.
La función de densidad de probabilidad normal
Una de las funciones de densidad de probabilidad más útiles es la función de densidad de probabilidad normal o gaussiana (a veces denominada curva de campana) definida como:
La curva gaussiana para una población con media μ y desviación estándar σ viene dada por\( f(x)=\frac{1}{σ\sqrt{2π}} e^{\frac{−(x−μ)^2}{(2σ2)}} \nonumber\), donde el factor\( \frac{1}{(σ\sqrt{2π})} \nonumber\) se llama la constante de normalización, que es necesaria para hacer que la probabilidad sobre todo el espacio sea igual a 1.
La función de densidad tiene la forma de curva de campana representada a continuación:
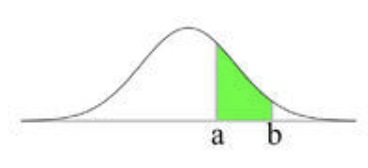
Esta función permite describir una población completa a partir de mediciones estadísticas tomadas de una pequeña muestra de la población. Las únicas medidas necesarias son la media (μ) y la desviación estándar (σ). Una vez que se conocen esos dos números, se define la curva normal.
Supongamos que las cajas que contienen 100 bolsitas de té tienen un peso medio de 10.2 onzas cada una y una desviación estándar de 0.1 onzas. ¿Qué porcentaje de todas las cajas se espera que pese entre 10 y 10.5 onzas? ¿Cuál es la probabilidad de que una caja pese menos de 10 onzas? ¿Cuál es la probabilidad de que una caja pese exactamente 10 onzas?
Usando la función de densidad de probabilidad normal,\( f(x)=\frac{1}{σ\sqrt{2π}} e^{\frac{−(x−μ)^2}{(2σ^2)}} \nonumber\).
Sustituyendo μ=10.2 y σ=0.1, obtenemos
\[ f(x)=\frac{1}{(0.1)\sqrt{2π}} e^{\frac{−(x−10.2)^2}{(2(0.1)^2)}} \nonumber\].
El porcentaje de todas las cajas de té que se espera que pesen entre 10 y 10.5 onzas se puede calcular como
\( P(10≤x≤10.5) = \int\limits_10^10.5 \frac{1}{(0.1) \sqrt{2π}} e^{\frac{−(x−10.2)^2}{(2(0.1)^2)}} dx \nonumber\).
La integral de\( e^{x^2} \nonumber\) no tiene un antiderivado elemental y por lo tanto no puede ser evaluada por técnicas estándar. Sin embargo, podemos utilizar técnicas numéricas, como La regla de Simpson o La regla trapezoidal, para encontrar un valor aproximado (pero muy preciso). Usando la función de programación de una calculadora científica o, software matemático, eventualmente obtenemos
\( \int\limits_{10}^{10.51} \frac{1}{(0.1)\sqrt{2π}} e^{\frac{−(x−10.2)^2}{(2(0.1)^2)}}dx≈0.976 \mbox{ That is, } P(10≤x≤10.5)≈0.976 \nonumber\).
Nota Tecnológica: Para realizar este cálculo con una calculadora gráfica de la familia TI-83/84, haga lo siguiente:
En el menú [DISTR.CR.T] (Figura 6.11.4) seleccione la opción 2, que pone la frase “normalcdf” en la pantalla de inicio. Agregue el límite inferior, el límite superior, la media, la desviación estándar, separados por comas, cierre los paréntesis y presione [ENTRAR]. El resultado se muestra en la Figura 6.11.5.
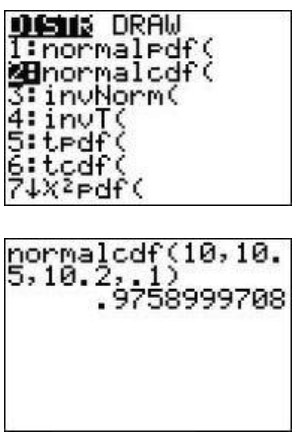
Para la probabilidad de que una caja pese menos de 10.2 onzas, usamos el área bajo la curva a la izquierda de x=10.2.
Integrando numéricamente, obtenemos
\[ P(9≤x≤10) = \int\limits_9^{10} \frac{1}{(0.1)\sqrt{2π}} e^{\frac{−(x−10.2)^2}{(2(0.1)^2)}} dx \nonumber\]
\[ P(9≤x≤10.2)≈0.02275 \nonumber\]
\[=2.28%, \nonumber\]
que dice que esperaríamos que 2.28% de las cajas pesen menos de 10 onzas.
Teóricamente la probabilidad aquí será exactamente cero porque estaremos integrando de 10 a 10 que es cero. Sin embargo, dado que todas las escalas tienen algún error (llámalo), prácticamente encontraríamos la probabilidad de que el peso caiga entre 10−y 10+.
Ejemplos
Ejemplo 1
Anteriormente, se le pidió que determinara qué tipo de variable aleatoria (discreta o continua) se asociaría con probabilidades calculadas usando integrales definidas.
Si dijeras que la variable aleatoria continua estaría asociada con probabilidades determinadas por integrales definidas, estarías en lo correcto.
Ejemplo 2
Un cociente de inteligencia o coeficiente intelectual es una puntuación derivada de diferentes pruebas estandarizadas que intentan medir el nivel de inteligencia de un ser humano adulto. El puntaje promedio de la prueba es de 100 y la desviación estándar es de 15. ¿Cuál es el porcentaje de la población que tiene una puntuación entre 85 y 115? ¿Qué porcentaje de la población tiene una puntuación superior a 140?
Usando la función de densidad de probabilidad normal\( f(x) = \frac{1}{σ \sqrt{2π}} e^{ \frac{−(x−μ)^2}{(2σ^2)}} \nonumber\),
y sustituyendo\( μ=100 \mbox{ and } σ=15, f(x)= \frac{1}{15\sqrt{2π}}e^{\frac{−(x−100)^2}{(2(15)^2)}} \nonumber\).
El porcentaje de la población que tiene una puntuación entre 85 y 115 es\( P(85≤x≤115)= \int\limits_85^115 \frac{1}{15\sqrt{2π}} e^{ \frac{−(x−100)^2}{(2(15)^2)}} \nonumber\).
Nuevamente, la integral de\( e^{−x^2} \nonumber\) no tiene un antiderivado elemental y por lo tanto no puede ser evaluada. Usando la función de programación de una calculadora científica o un software de computadora matemático, obtenemos\( \int\limits_85^115 \frac{1}{15\sqrt{2π}}e^{−(x−100)^2}{(2(15)^2)} dx≈0.68 \nonumber\). Es decir,\( P(85≤x≤115)≈68% \nonumber\)
Que dice que 68% de la población tiene un puntaje de CI entre 85 y 115.
Para medir la probabilidad de que una persona seleccionada aleatoriamente tenga un puntaje de CI superior a 140,\( P(x≥140)= \int\limits_{140}^\infty \frac{1}{15\sqrt{2π}}e^{\frac{−(x−100)^2}{(2(15)^2)}} dx \nonumber\)
Esta integral es aún más difícil de integrar ya que es una integral impropia. Para evitar el trabajo desordenado, podemos argumentar que como es extremadamente raro conocer a alguien con un puntaje de CI superior a 200 podemos aproximar la integral de 140 a 200 Entonces
\( P(x≥140) = \int\limits_{140}^{200} \frac{1}{15\sqrt{2π}}e^{\frac{−(x−100)^2}{(2(15)^2)}} dx \nonumber\)
Integrando numéricamente, obtenemos P (x≥140) ≈0.0039.
Por lo que la probabilidad de seleccionar al azar a una persona con un puntaje de CI superior a 140 es de 0.0039. ¡Eso es aproximadamente una persona por cada 250 individuos!
Revisar
Para #1 -4, encuentre el número r que hace de la función una función de densidad de probabilidad sobre el espacio de muestra dado.
- \( f(x)=r \nonumber\)sobre el espacio muestral de [-7, 7].
- \( f(x)=rx(x−5) \nonumber\)sobre el espacio muestral de [0, 5].
- \( f(x)= \frac{r}{(1+x)^2} \nonumber\)sobre el espacio muestral de [0, 25].
- \( f(x)=rsinx \nonumber\)sobre el espacio muestral de\( [0, \frac{π}{2}] \nonumber\).
- Dada una función de densidad de probabilidad triangular g (x) sobre el espacio muestral [0, 10], ¿cuál es el valor más alto de g (x) si ocurre en x=7?
- ¿Podría la función\( g(x)=\frac{−4}{25}x+0.9 \nonumber\) ser una función de densidad de probabilidad en el intervalo [0, 10]?
- Supongamos que f (x) es la función de densidad de probabilidad para la vida útil de una bombilla del fabricante, donde x se mide en horas. Explicar el significado de cada integral.
- \( \int_1000^5000 f(x)dx \nonumber\)
- \( \int_3000^∞ f(x)dx \nonumber\)
- Supongamos que\( f(x)=−\frac{1}{36}(x^2−9) \nonumber\) es la función de densidad de probabilidad para el tiempo de ocurrencia de un evento dentro de la ventana de tiempo [-3, +3 horas] (0 es la ocurrencia de tiempo). ¿Cuál es la probabilidad de que el evento ocurra dentro de ±1 hora del tiempo esperado?
- Para el problema #8, ¿qué ventana de tiempo garantiza un 90% de probabilidad de ocurrencia?
- El tiempo que un cliente pasa esperando hasta que su entrada se sirve en un determinado restaurante está modelado por una función de densidad exponencial\( f(x)=0.125e^{−0.125t} \nonumber\), donde\( \frac{1}{0.125}=8\nonumber\) es el tiempo de espera promedio en minutos.
- ¿Cuál es la probabilidad de que un cliente sea atendido en los primeros 3 minutos?
- ¿Cuál es la probabilidad de que un cliente tenga que esperar más de 10 minutos?
- La estatura promedio de una hembra adulta en Los Ángeles es de 63.4 pulgadas (5 pies, 3.4 pulgadas) con una desviación estándar de 3.2 pulgadas.
- ¿Cuál es la probabilidad de que la estatura de una hembra sea inferior a 63.4 pulgadas?
- ¿Cuál es la probabilidad de que la estatura de una hembra esté entre 63 y 65 pulgadas?
- ¿Cuál es la probabilidad de que la estatura de una hembra sea de más de 6 pies?
- ¿Cuál es la probabilidad de que la estatura de una hembra sea exactamente de 5 pies?
- La mediana de una distribución con una función de densidad de probabilidad f (x), es el valor M tal que\( \int_{-∞}^M f(x)dx=0.5 \nonumber\). La mitad de los valores de la distribución estarán por encima de M, y la mitad estará por debajo de M. Encuentre el valor mediano para cada una de las siguientes funciones de densidad de probabilidad:
- \( f(x)=−\frac{1}{36} (x^2−9) \nonumber\)sobre el intervalo [-3, 3].
- \( f(x)=0.125e^{−0.125t} \nonumber\)sobre el intervalo [0, ∞).
- La media de una distribución con la función de densidad de probabilidad f (x), es el valor dado por\( \int_{−∞}^∞ xf(x)dx \nonumber\). Encuentre el valor medio para cada una de las siguientes funciones de densidad de probabilidad:
- \( f(x)=−\frac{1}{36}(x^2−9) \nonumber\)sobre el intervalo [-3, 3].
- \( f(x)=0.125e^{−0.125t} \nonumber\)sobre el intervalo [0, ∞).
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 6.10.
El vocabulario
| Término | Definición |
|---|---|
| Función de densidad de probabilidad gaussiana | Un pdf normal (gaussiano) es un pdf continuo definido por f (x) =1σ2π√e− (x−μ) 2 (2σ2) donde μ es la media y σ es la desviación estándar. |
| media | La media de una distribución con la función de densidad de probabilidad f (x) es el valor dado por −∞ ∞ xf (x) dx. |
| mediana | La mediana de una distribución con una función de densidad de probabilidad f (x) es el valor M tal que −∞ Mf (x) dx=0.5. La mitad de los valores de la distribución estarán por encima de M, y la mitad estará por debajo de M. |
| función de densidad de probabilidad normal | Un pdf normal (gaussiano) es un pdf continuo definido por f (x) =1σ2π√e− (x−μ) 2 (2σ2) donde μ es la media y σ es la desviación estándar. |
| Una función f (x) se denomina función de densidad de probabilidad (pdf) si f (x) ≥0 para todos x, el área debajo de la gráfica de f (x) sobre todos los números reales es exactamente 1, y la probabilidad de que x esté en el intervalo [a, b] es P (a≤x≤b) =abf (x) dx. | |
| Probabilidad | La probabilidad es la posibilidad de que algo suceda. Se puede escribir como fracción, decimal o por ciento. |
| función de densidad de probabilidad | Una función f (x) se denomina función de densidad de probabilidad si f (x) ≥0 para todos x, el área debajo de la gráfica de f (x) sobre todos los números reales es exactamente 1, y la probabilidad de que x esté en el intervalo [a, b] es P (a≤x≤b) =abf (x) dx. |
| función de densidad de probabilidad triangular | Una función de densidad de probabilidad triangular (pdf) es un pdf continuo cuya forma triangular está definida por tres valores de x: un valor inferior, un valor de modo con el valor de distribución más alto y un valor superior. |
| función de densidad de probabilidad uniforme | Una función de densidad de probabilidad uniforme (o rectangular, plana) (pdf) P (x) es una distribución continua donde cada intervalo igual de x tiene la misma probabilidad. |
Recursos adicionales
Video: Más sobre las funciones de densidad de probabilidad
Mundo real: Muertes prevenibles

