1.3:1.3 Notación de puntos y notación de funciones
- Page ID
- 107316
Al realizar múltiples transformaciones, es muy fácil cometer un pequeño error. Esto es especialmente cierto cuando intentas hacer cada paso mentalmente. La notación de puntos es una herramienta útil para concentrar tus esfuerzos en un solo punto y te ayuda a evitar cometer pequeños errores.
¿Cómo\(f(3 x)+7\) se vería en la notación puntual y por qué es útil?
Uso de la notación de funciones y notación de puntos
Una transformación se puede escribir en notación de funciones y en notación de puntos. La notación de funciones es muy común y práctica porque permite graficar cualquier función usando el mismo proceso de pensamiento básico que se necesita para graficar una parábola en forma de vértice.
Otra forma de graficar una función es transformar cada punto uno a la vez. Este método funciona bien cuando una tabla de\(x, y\) valores está disponible o se identifica fácilmente a partir de la gráfica.
Esencialmente, toma cada coordenada\((x, y)\) y asigna una nueva coordenada basada en la transformación.
\((x, y) \longrightarrow(\)nuevo\(x,\) nuevo\(y)\)
Esta notación se llama notación puntual. La nueva\(y\) coordenada es directa y es directamente de lo que ocurre afuera\(f(x)\) porque\(f(x)\) es solo otra forma de escribir\(y\). Por ejemplo,\(f(x) \rightarrow 2 f(x)-1\) tendría una nueva\(y\) coordenada de\(2 y-1\).
La nueva\(x\) coordenada es más problemática. Viene de deshacer las operaciones que afectan\(x\). Por ejemplo,\(f(x) \rightarrow f(2 x-1)\) tendría una nueva\(x\) coordenada de\(\frac{x+1}{2}\)
Las representaciones de notación de función y notación de puntos de la transformación “Desplazamiento horizontal a la derecha tres unidades, desplazamiento vertical hacia arriba 4 unidades” son
\(f(x) \rightarrow f(x-3)+4\)
\((x, y) \rightarrow(x+3, y+4)\)
Observe que las operaciones con el\(x\) son diferentes.
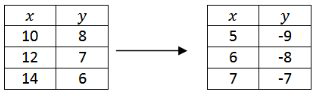
Aplicar la transformación anterior a la siguiente tabla de puntos.
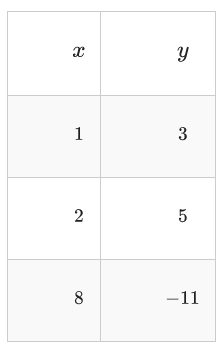
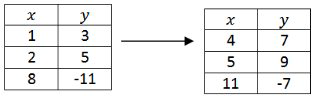
Observe que la notación puntual reduce en gran medida la visualización mental requerida para mantener todas las transformaciones rectas a la vez.
Ejemplos
Anteriormente, se le preguntó cuál\(f(3 x)+7\) sería la función cuando se escribiera en notación puntual. Cuando se escribe en notación puntual, se escribiría como\((x, y) \rightarrow\left(\frac{x}{3}, y+7\right) .\) Esto es útil porque resulta obvio que los\(x\) valores están todos divididos por tres y todos los\(y\) valores aumentan en 7.
Convierta la siguiente función en notación de puntos a palabras y luego notación de función.
\((x, y) \rightarrow(3 x+1,-y+7)\)
Estiramiento horizontal por un factor de 3 y luego un desplazamiento horizontal hacia la derecha una unidad. Reflexión vertical sobre el\(x\) eje y luego un desplazamiento vertical 7 unidades hacia arriba.
\(f(x) \rightarrow-f\left(\frac{1}{3} x-\frac{1}{3}\right)+7\)
Convierte la siguiente notación de función en palabras y luego notación de puntos. Por último, aplicar la transformación a tres puntos de ejemplo.
\(f(x) \rightarrow-2 f(x-1)+4\)
Reflexión vertical a través del\(x\) eje. Estiramiento vertical por un factor de
Desplazamiento\(2 .\) vertical 4 unidades. Desplazamiento horizontal a la derecha una unidad.
\((x, y) \rightarrow(x+1,-2 y+4)\)

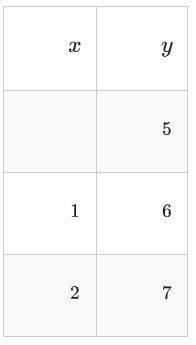
Convertir la siguiente notación de función en notación de puntos y aplicarla a la tabla de puntos incluida
\(f(x) \rightarrow \frac{1}{4} f(-x-3)-1\)
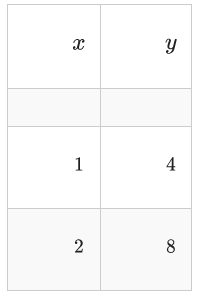
El\(y\) componente puede ser observado directamente. Para el\(x\) componente es necesario deshacer el argumento. \((x, y) \rightarrow\left(-x-3, \frac{1}{4} y-1\right)\)
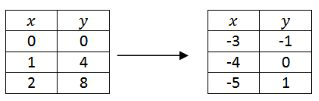
Convierta la siguiente notación de puntos a palabras y a notación de función y luego aplique la transformación a la tabla de puntos incluida.
\((x+3, y-1) \rightarrow(2 x+6,-y)\)
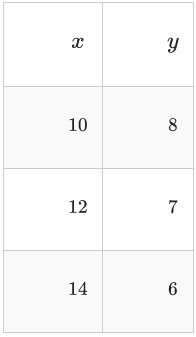
Este problema es diferente porque parece que hay una transformación
pasando al punto izquierdo original. Esta es una capa añadida de desafío
porque la transformación del interés es solo la diferencia entre los dos
puntos. Observe que la\(x\) coordenada simplemente se ha duplicado y la\(y\)
coordenada se ha hecho más grande en uno y se ha vuelto negativa. Este problema puede
ser reescrito como:
\((x, y) \rightarrow(2 x,-(y+1))=(2 x,-y-1)\)
\(f(x) \rightarrow-f\left(\frac{x}{2}\right)-1\)
Revisar
Convierte la siguiente notación de función en palabras y luego notación de puntos. Por último, aplicar la transformación a tres puntos de ejemplo.
1. 9\(f(x) \rightarrow-\frac{1}{2} f(x+1)\)
2. \(g(x) \rightarrow 2 g(3 x)+2\)
3. \(h(x) \rightarrow-h(x-4)-3\)
4. \(j(x) \rightarrow 3 j(2 x-4)+1\)
5. \(k(x) \rightarrow-k(x-3)\)
Convierta las siguientes funciones en notación de puntos a notación de función.
6. \((x, y) \rightarrow\left(\frac{1}{2} x+3, y-4\right)\)
7. \((x, y) \rightarrow(2 x+4,-y+1)\)
8. \((x, y) \rightarrow(4 x, 3 y-5)\)
9. \((2 x, y) \rightarrow(4 x,-y+1)\)
10. \((x+1, y-2) \rightarrow(3 x+3,-y+3)\)
Convierta las siguientes funciones en notación de funciones a notación de puntos.
11. \(f(x) \rightarrow 3 f(x-2)+1\)
12. \(g(x) \rightarrow-4 g(x-1)+3\)
13. \(h(x) \rightarrow \frac{1}{2} h(2 x+2)-5\)
14. \(j(x) \rightarrow 5 j\left(\frac{1}{2} x-2\right)-1\)
15. \(k(x) \rightarrow \frac{1}{4} k(2 x-4)\)

