2.3: Expansión polinomial y Triángulo de Pascal

La expresión\((2 x+3)^{5}\) tardaría un tiempo en multiplicarse. ¿Hay algún patrón que puedas usar?

Expansión con el Triángulo de Pascal

Expansión de un binomio

Pascal era un matemático francés en el\(17^{t h}\) siglo, pero el triángulo ahora llamado Triángulo de Pascal se estudió mucho antes de que Pascal lo usara. El patrón se utilizó alrededor del\(10^{t h}\) siglo en Persia, India y China, así como en muchos otros lugares.

El propósito principal de usar este triángulo es introducir cómo expandir binomios.

\((x+y)^{0}=1\)
\((x+y)^{1}=x+y\)
\((x+y)^{2}=x^{2}+2 y+y^{2}\)
\((x+y)^{3}=x^{3}+3 x^{2} y+3 x y^{2}+y^{3}\)

Observe que los coeficientes para los\(y\) términos\(x\) y del lado derecho se alinean exactamente con los números del triángulo de Pascal. Esto quiere decir que dada\((x+y)^{n}\) para cualquier potencia se\(n\) puede escribir la expansión usando los coeficientes del triángulo. Tenga en cuenta que para escribir los coeficientes para cualquier potencia\(n\), es necesario mirar la fila\(n+1\) para encontrar los coeficientes.

Si te pidieran expandir\((3 x-2)^{4}\) usando el Triángulo de Pascal, mirarías la fila 5 para encontrar los coeficientes. Los coeficientes serán 1,4,6,4,\(1 ;\) sin embargo, ya que ya hay coeficientes con el\(x\) y el término constante hay que tener especial cuidado.

\(1 \cdot(3 x)^{4}+4 \cdot(3 x)^{3} \cdot(-2)+6 \cdot(3 x)^{2} \cdot(-2)^{2}+4 \cdot(3 x) \cdot(-2)^{3}+1 \cdot(-2)^{4}\)

Entonces sólo se trata de multiplicar y hacer un seguimiento de los signos negativos.

\(81 x^{4}-216 x^{3}+216 x^{2}-96 x+16\)

Cuando estudies cómo contar con combinaciones entonces podrás calcular el valor de cualquier coeficiente sin escribir todo el triángulo.

Patrones y Triángulo de Pascal

Hay muchos patrones en el triángulo. Éstos son solo algunos.

1. Observe la forma en que se crea cada número sumando los dos números anteriores en el lado izquierdo y derecho.
2. A medida que vas más abajo del triángulo los valores en una fila se acercan a una curva de campana. Esto está estrechamente relacionado con la distribución normal en la estadística.
3. Para cualquier fila que tenga un segundo término que sea primo, todos los números además de 1 en esa fila son divisibles por ese número primo.

Uso de la vida real: En el juego Plinko donde un objeto se deja caer a través de una matriz triangular de clavijas, la probabilidad (que corresponde proporcionalmente a los valores en el triángulo) de aterrizar hacia el centro es mayor que aterrizar hacia el borde. Esto se debe a que cada número en el triángulo indica el número de formas en que un objeto que cae puede llegar a ese espacio a través de los números anteriores.

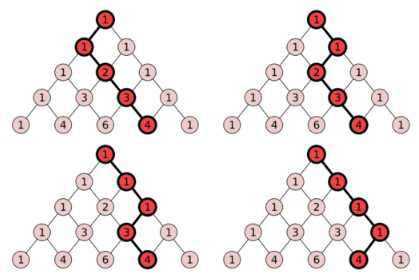
Ejemplos

Ejemplo 1

Antes, se le pidió que se multiplicara\((2 x+3)^{5}\). El triángulo de Pascal permite identificar que los coeficientes de\((2x+3)^{5}\) serán\(1,5,10,10,5,1 .\) Al sustituir cuidadosamente, la expansión será:

\(1 \cdot(2 x)^{5}+5 \cdot(2 x)^{4} \cdot 3+10 \cdot(2 x)^{3} \cdot 3^{2}+10 \cdot\left(2 x^{2}\right) \cdot 3^{3}+5(2 x)^{1} \cdot 3^{4}+3^{5}\)

Simplificar es cuestión de aritmética, pero la mayor parte del trabajo se realiza gracias a los patrones del Triángulo de Pascal.

Ejemplo 2

Facturar el siguiente polinomio reconociendo los coeficientes.

\(x^{4}+4 x^{3}+6 x^{2}+4 x+1\)

Los coeficientes son 1, 4, 6, 4 y 1 y esos coeficientes están en la quinta fila. La primera fila del Triángulo de Pascal muestra los coeficientes para la potencia 0 por lo que la quinta fila muestra los coeficientes para la 4ª potencia. Así, la forma factorizada es:

\((x+1)^{4}\)

Ejemplo 3

Facturar el siguiente polinomio reconociendo los coeficientes.

\(8 x^{3}-12 x^{2}+6 x-1\)

ya que el primer coeficiente no es 1, es necesario tomar la raíz apropiada del primer término de la expresión para encontrar el primer término del binomio. En este caso, el primer término del binomio debe ser\(2 x\). También, el último término debe ser -1 y el poder debe ser\(3 .\) Ahora todo lo que queda es verificar.

\((2 x-1)^{3}=(2 x)^{3}+3(2 x)^{2} \cdot(-1)+3(2 x)^{1}(-1)^{2}+(-1)^{3}=8 x^{3}-12 x^{2}+6 x-1\)

Ejemplo 4

Amplíe el siguiente binomio:\(\left(\frac{1}{2} x-3\right)^{5}\)

Sabes que los coeficientes serán 1, 5, 10, 10, 5, 1.

\(1\left(\frac{1}{2} x\right)^{5}+5\left(\frac{1}{2} x\right)^{4}(-3)+10\left(\frac{1}{2} x\right)^{3}(-3)^{2}+10\left(\frac{1}{2} x\right)^{2}(-3)^{3}+5\left(\frac{1}{2} x\right)(-3)^{4}+1 \cdot(-3)^{5}\)

\(=\frac{x^{5}}{32}-\frac{15 x^{4}}{16}+\frac{90 x^{3}}{8}-\frac{270 x^{2}}{4}+\frac{405 x}{2}-243\)

Recuerda simplificar las fracciones.

\(=\frac{x^{5}}{32}-\frac{15 x^{4}}{16}+\frac{45 x^{3}}{4}-\frac{135 x^{2}}{2}+\frac{405 x}{2}-243\)

Ejemplo 5

Ampliar el siguiente trinomio:\((x+y+z)^{4}\)

Desafortunadamente, el triángulo de Pascal no se aplica a los trinomios. En lugar de pensar en un triángulo bidimensional, se nearía a calcular una pirámide tridimensional que se llama Pirámide de Pascal. La suma de los cinco términos a continuación es su respuesta.

\(1 x^{4}+4 x^{3} z+6 x^{2} z^{2}+4 x z^{3}+1 z^{4}\)
\(4 x^{3} y+12 x^{2} y z+12 x y z^{2}+4 y z^{3}\)
\(6 x^{2} y^{2}+12 x y^{2} z+6 y^{2} z^{2}\)
\(4 x y^{3}+4 y^{3} z\)
\(1 y^{4}\)

Observe cuántos patrones existen en los coeficientes de esta capa de la pirámide.

Revisar

Facturar los siguientes polinomios reconociendo los coeficientes.

1. \(x^{2}+2 x y+y^{2}\)

2. \(x^{3}+3 x^{2}+3 x+1\)

3. \(x^{5}+5 x^{4}+10 x^{3}+10 x^{2}+5 x+1\)

4. \(27 x^{3}-27 x^{2}+9 x-1\)

5. \(x^{3}+12 x^{2}+48 x+64\)

Expande los siguientes binomios usando el Triángulo de Pascal.

6. \((2 x-3)^{3}\)

7. \((3 x+4)^{4}\)

8. \((x-y)^{7}\)

9. \((a+b)^{10}\)

10. \((2 x+5)^{5}\)

11. \((4 x-1)^{4}\)

12. \((5 x+2)^{3}\)

13. \((x+y)^{6}\)

14. \((3 x+2 y)^{3}\)

15. \((5 x-2 y)^{4}\)