2.2.6: Funciones de trigonometría inversa usando álgebra
- Page ID
- 107707
“Deshacer” una función cambiando\(x\) y\(y\) valores y resolviendo para\(y\).
Si te dieron una función, como\(f(x)=\dfrac{2x}{x+7}\), ¿puedes decir si la función tiene una inversa? ¿Hay alguna manera de que puedas encontrar su inversa a través de la manipulación algebraica?
Encontrar la inversa de una función
Un “inverso” es algo que deshace una función, devolviendo el argumento original. Por ejemplo, una función como\(y=\dfrac{1}{3}x\) tiene una función inversa de\(y=3x\), ya que cualquier valor colocado en la primera función será devuelto como lo que originalmente era si se introduce en la segunda función. En este caso, es fácil ver que para “deshacer” la multiplicación por\(\dfrac{1}{3}\), se debe multiplicar por 3. Sin embargo, en muchos casos puede no ser fácil inferir por examen cuál es la inversa de una función.
Para comenzar, examinemos qué se requiere para que una función tenga una inversa. Es importante recordar que cada función tiene una relación inversa y que esta relación inversa es una función sólo si la función original es uno a uno. Una función es uno a uno cuando su gráfica pasa tanto la prueba de línea vertical como la horizontal. Esto significa que cada línea vertical y horizontal cruzará la gráfica exactamente en un lugar.
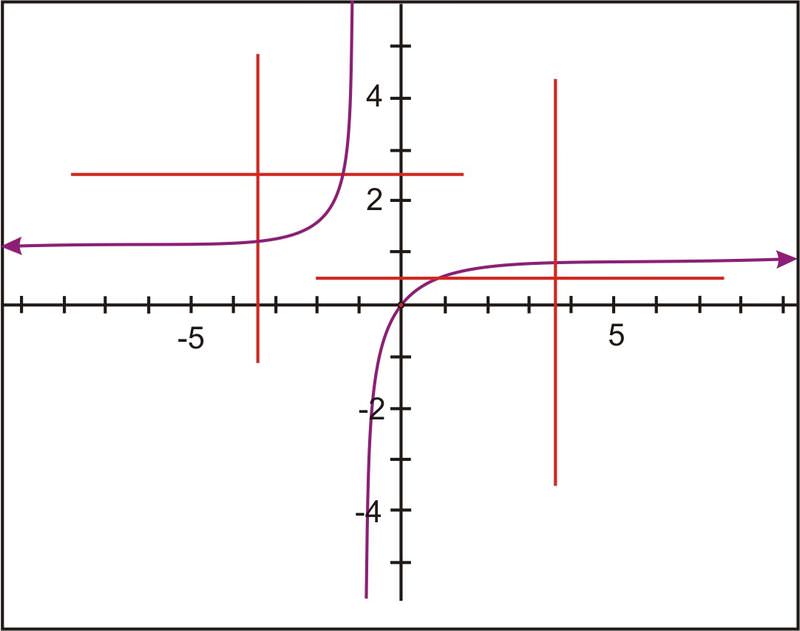
Esta es la gráfica de\(f(x)=\dfrac{x}{x+1}\). La gráfica sugiere que\(f\) es uno a uno porque pasa tanto las pruebas de línea vertical como horizontal. Para encontrar la inversa de\(f\), cambiar el\(x\) y\(y\) y resolver para\(y\).
Primero, cambiar\(x\) y\(y\).
\(x=\dfrac{y}{y+1}\)
A continuación, multiplique ambos lados por\((y+1)\).
\(\begin{aligned} (y+1)x&=\dfrac{y}{y+1}(y+1) \\ x(y+1)&=y \end{aligned}\)
Después, aplique la propiedad distributiva y ponga todos los términos y por un lado para que pueda sacar la y.
\(\begin{aligned} xy+x=y \\ xy−y=−x \\ y(x−1)=−x \end{aligned}\)
Dividir por\((x−1)\) para conseguir\(y\) por sí mismo.
\(y=\dfrac{−x}{x−1}\)
Por último, multiplicar el lado derecho por\(\dfrac{−1}{−1}\).
\(y=\dfrac{x}{1−x}\)
Por lo tanto la inversa de f es\(f^{−1}(x)=\dfrac{x}{1−x}\).
El símbolo\(f^{−1}\) se lee “f inverso” y no es el recíproco de f.
Encontrar la inversa de una función
1. Encuentra la inversa de\(f(x)=\dfrac{1}{x−5}\) algebraicamente.
Para encontrar la inversa algebraicamente, cambiar\(f(x)\) a\(y\) y luego cambiar\(x\) y\(y\).
\(\begin{aligned} y&=1x−5\\ x&=1y−5 \\ x(y−5)&=1 \\ xy−5x&=1 \\ xy&=5x+1 \\ y&=\dfrac{5x+1}{x}\end{aligned}\)
2. Encuentra la inversa de\(f(x)=5 \sin^{−1} (\dfrac{2}{x−3})\)
\ (\ begin {alineado}
f (x) &=5\ sin ^ {-1}\ izquierda (\ dfrac {2} {x-3}\ derecha)\\
x &=5\ sin ^ {-1}\ izquierda (\ dfrac {2} {y-3}\ derecha)\
\ dfrac {x} {5} &=\ sin ^ {-1}\ izquierda (\ dfrac {2} {y-3}\ derecha)\\
\ sin\ dfrac {x} {5} &=\ izquierda (\ dfrac {2} {y-3}\ derecha)\\
( y-3)\ sin\ dfrac {x} {5} &=2\\
(y-3) &=\ dfrac {2} {\ sin\ dfrac {x} {5}}\\
y &=\ dfrac {2} {\ sin\ dfrac {x} {5}} +3
\ final {alineado}\)
3. Encuentra la inversa de la función trigonométrica\(f(x)=4 \tan^{−1} (3x+4)\)
\ (\ begin {alineado}
x &=4\ tan ^ {-1} (3 y+4)\\
\ dfrac {x} {4} &=\ tan ^ {-1} (3 y+4)\\
\ tan\ dfrac {x} {4} &=3 y+4\
\\ tan\ dfrac {x} {4} -4 &=3 y\
\ dfrac {tan\\ dfrac {x} {4} -4} {3} &=y\\
f^ {-1} (x) &=\ dfrac {\ tan \ dfrac {x} {4} -4} {3}
\ final {alineado}\)
Anteriormente, se le pidió que encontrara la inversa de una función.
Solución
Dado que la función original es:
\(f(x)=y=\dfrac{2x}{x+7}\)
Primero puede cambiar todos los valores "" y\(x\) ""\(y\) "”:
\(x=\dfrac{2y}{y+7}\)
Luego puede reorganizar la ecuación y aislar “y”:
\ (\ begin {array} {r}
x (y+7) =2 y\\
x y+7 x=2 y\\
x y-2 y=-7 x\\
y (x-2) =-7 x\\
y=\ dfrac {-7 x} {x-2}
\ end {array}\)
La función inversa se escribe como\(f^{−1}(x)=\dfrac{−7x}{x−2}\)
Encuentra la inversa de\(f(x)=2x^3−5\)
Solución
\ (\ begin {alineado}
f (x) &=2 x^ {3} -5\\
y &=2 x^ {3} -5\\
x &=2 y^ {3} -5\\
x+5 &=2 y^ {3}
\\ dfrac {x+5} {2} &=y^ {3}\
\ sqrt [3] {\ dfrac {x+5} 2}} &=y
\ end {alineado}\)
Encuentra la inversa de\(y=\dfrac{1}{3} \tan^{−1}(\dfrac{3}{4} x−5)\)
Solución
\ (\ begin {alineado}
y &=\ dfrac {1} {3}\ tan ^ {-1}\ izquierda (\ dfrac {3} {4} x-5\ derecha)\\
x &=\ dfrac {1} {3}\ tan ^ {-1}\ izquierda (\ dfrac {3} {4} y-5\ derecha)\\
3 x &=\ tan ^ -1}\ izquierda (\ dfrac {3} {4} y-5\ derecha)\
\\ tan (3 x) &=\ dfrac {3} {4} y-5\
\ bronceado (3 x) +5 &=\ dfrac {3} {4} y\\
\ dfrac {4 (\ tan (3 x) +5)} {3} &=y
\ end {alineado}\)
Encuentra la inversa de\(g(x)=2 \sin(x−1)+4\)
Solución
\ (\ begin {alineado}
g (x) &=2\ sin (x-1) +4\\
y &=2\ sin (x-1) +4\\
x &=2\ sin (y-1) +4\\
x-4 &=2\ sin (y-1)\
\ dfrac {x-4} {2} &=\ sin (y-1)\\
1+\ sin ^ {-1}\ izquierda (\ dfrac {x-4} {2}\ derecha) &=y
\ fin {alineado}\)
Revisar
Encuentra la inversa de cada función.
- \(f(x)=3x+5\)
- \(g(x)=0.2x−7\)
- \(h(x)=0.1x^2\)
- \(k(x)=5x+6\)
- \(f(x)=\sqrt{x−4}\)
- \(g(x)=(x)^{\dfrac{1}{3}}+1\)
- \(h(x)=(x+1)^3\)
- \(k(x)=\dfrac{x^2}{3}\)
- \(f(x)=−2+4 \sin^{−1} (x+7)\)
- \(g(x)=1+3 \tan^{−1}(2x+1)\)
- \(h(x)=4 \cos^{−1}(3x)\)
- \(k(x)=−1 \tan^{−1} (6x)\)
- \(j(x)=5+2 \sin^{−1}(x+5)\)
- \(m(x)=−2 \tan (3x+1)\)
- \(p(x)=5−6 \sin(\dfrac{x}{2})\)
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 4.3.
El vocabulario
| Término | Definición |
|---|---|
| Prueba de Línea Horizontal | La prueba de línea horizontal dice que si una línea horizontal dibujada en cualquier lugar a través del gráfico de una función interseca la función en más de una ubicación, entonces la función no es uno a uno y no es invertible. |
| Función Uno a Uno | Una función es uno a uno si su inversa es también una función. Una función uno a uno pasa las pruebas de línea horizontal y vertical. |
| Prueba de línea vertical | La prueba de línea vertical dice que si una línea vertical dibujada en cualquier parte a través de la gráfica de una relación interseca la relación en más de una ubicación, entonces la relación no es una función. |
Recursos adicionales
Video: Funciones inversas

