2.6.9: Gráficas Sinusoidales Generales
- Page ID
- 107642
seno y coseno y su relación con el círculo unitario.
La función coseno son las coordenadas x del círculo unitario y la función sinusoidal son las coordenadas y. ya que el círculo unitario tiene el radio uno y está centrado en el origen, tanto el seno como el coseno oscilan entre el positivo y el negativo.
¿Qué sucede cuando el círculo no está centrado en el origen y no tiene un radio de 1?
Gráficas de Funciones sinusoidales
La familia de funciones sinusoidales se refiere a ondas sinusoidales o cosenoidales ya que son las mismas excepto por un desplazamiento horizontal. Esta familia de funciones también se llama familia de funciones periódicas porque la función se repite después de un período de tiempo determinado.
Considera una noria que gira uniformemente con un radio de 1 unidad. Comienza en (1, 0) o un ángulo de 0 radianes y gira en sentido antihorario a una velocidad de un ciclo por\(2\pi \) minuto (para que puedas usar el tiempo es igual a radianes).
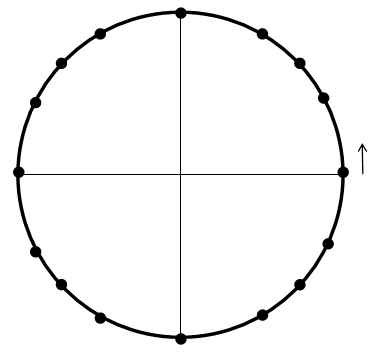
Se eligen los 16 puntos alrededor del círculo porque corresponden a los puntos clave del círculo unitario. Sus alturas (valores y) y anchuras (valores x) ya son conocidas y se pueden rellenar.
Primero considere la altura en cada uno de los puntos a medida que viaja alrededor de la mitad del círculo desde la ubicación inicial. Lleve un registro de su trabajo en una mesa.
| Ángulo (radianes) | Altura (unidades) |
| 0 | 0 |
| \(\dfrac{\pi }{6}\) | \(\dfrac{1}{2}\) |
| \(\dfrac{\pi }{4}\) | \(\dfrac{\sqrt{2}}{2}\approx 0.707\) |
| \(\dfrac{\pi }{3}\) | \(\dfrac{\sqrt{3}}{2}\approx 0.866\) |
| \(\dfrac{\pi}{2}\) | 1 |
| \(\dfrac{2\pi }{3}\) | \(\dfrac{\sqrt{3}}{2}\approx 0.866\) |
| \(\dfrac{3\pi }{4}\) | \(\dfrac{\sqrt{2}}{2}\approx 0.707\) |
| \(\dfrac{5\pi }{6}\) | \(\dfrac{1}{2}\) |
| \(\pi\) | 0 |
Observe la simetría de la altura alrededor\(\dfrac{\pi}{2}\) y vea el resto de la tabla en los ejemplos. Una vez terminada la tabla, se pueden trazar estos puntos en un plano de coordenadas regular donde el eje x es el ángulo y el eje y es la altura. Esta es la primera parte de la gráfica de la función sinusoidal.
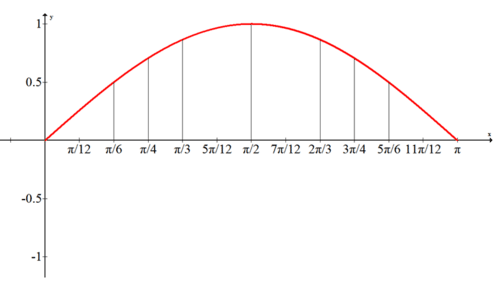
Para terminar la gráfica de la función sinusoidal, terminar la tabla de alturas de los puntos en los cuadrantes III y IV y dibujar un ciclo completo (conocido como periodo) de la función sinusoidal.
| Ángulo (radianes) | Altura (unidades) |
| \(\pi\) | 0 |
| \(\dfrac{7\pi }{6}\) | \(−\dfrac{1}{2}\) |
| \(\dfrac{5\pi }{4}\) | \(−\dfrac{\sqrt{2}}{2}\approx −0.707\) |
| \(\dfrac{4\pi }{3}\) | \(−\dfrac{\sqrt{3}}{2}\approx −0.866\) |
| \(\dfrac{3\pi}{2}\) | -1 |
| \(\dfrac{5\pi }{3}\) | \(−\dfrac{\sqrt{3}}{2}\approx −0.866\) |
| \(\dfrac{7 \pi}{4}\) | \(−\dfrac{\sqrt{2}}{2}\approx −0.707\) |
| \(\dfrac{11 \pi}{6}\) | \(−\dfrac{1}{2}\) |
| \(2\pi\) |
0 |
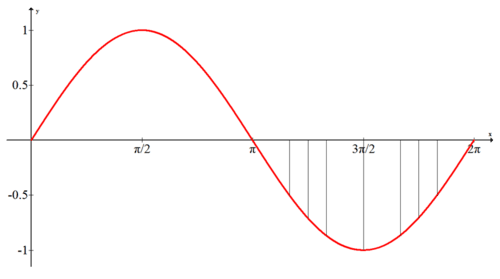
Similar al seno, puedes usar tu conocimiento de los ángulos 0,\(\dfrac{\pi}{2}\),\(\pi \)\(\dfrac{3\pi}{2}\),\(2\pi \) en el círculo unitario para obtener un ciclo completo de la gráfica coseno. Mientras que la función seno usa las coordenadas y, la función coseno son las coordenadas x del círculo unitario y mide el ancho. Al hacer referencia a un círculo unitario o a tu memoria, puedes llenar una tabla mucho más corta que antes.
| Ángulo (radianes) | Ancho (unidades) |
| 0 | 1 |
| \(\dfrac{\pi}{2}\) | 0 |
| \(\pi\) | -1 |
| \(\dfrac{3\pi}{2}\) | 0 |
| \(2\pi\) | 1 |
Primero grafica estos cinco puntos y luego conéctelos con una curva suave. Esto producirá la gráfica coseno.
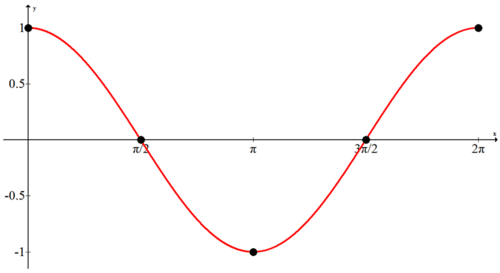
Determinar estos cinco puntos principales es la clave para graficar gráficas de seno o coseno incluso cuando la gráfica está desplazada o estirada.
Anteriormente, se le preguntó qué sucede cuando el círculo no está centrado en el origen y no tiene un radio de 1.
Solución
El círculo unitario produce las gráficas de seno y coseno de función padre. Cuando el círculo unitario se desplaza hacia arriba o hacia abajo, se hace más ancho o más estrecho, o se gira más rápido o más lento en cualquier dirección, entonces las gráficas de las funciones seno y coseno se transformarán usando reglas básicas de transformación de funciones.
¿Qué sucede a ambos lados de las gráficas de seno y coseno? ¿Puedes explicar por qué?
Solución
Las gráficas de las funciones seno (azul) y coseno (rojo) se repiten para siempre en ambas direcciones.


Si piensas en el ejemplo con la noria, el paseo seguirá dando vueltas y ha estado girando desde siempre. Es por ello que el mismo ciclo de la gráfica se repite una y otra vez.
¿Cómo son iguales los gráficos de seno y coseno y en qué se diferencian?
Solución
La gráfica sinusoidal es la misma que la gráfica coseno desplazada por\(\dfrac{\pi}{2}\). Además del desplazamiento, ambas curvas son idénticas debido a la perfecta simetría de los círculos.
¿Dónde están dos máximos y dos mínimos de la gráfica sinusoidal?

Solución
Un máximo de la gráfica sinusoidal ocurre en\(\left(\dfrac{\pi}{2}, 1\right)\). Un mínimo ocurre en\(\left(\dfrac{3\pi}{2}, −1 \right)\). Este es un ciclo de la gráfica sinusoidal. Ya que completa un ciclo cada vez\(2\pi \), cuando añades\(2\pi \) a una coordenada x estarás en el mismo punto del ciclo dándote otro máximo o mínimo.
\(\left(\dfrac{5\pi}{2},1\right)\)es otro máximo. \(\left(\dfrac{7\pi}{2},−1\right)\)es otro mínimo.
En el intervalo ¿\([−2\pi ,4\pi )\)dónde tiene ceros el coseno?
Solución
Observe dónde la curva coseno tiene coordenadas x iguales a cero. Tenga en cuenta que 4\ pi está excluido del intervalo. Los valores son\(−\dfrac{3\pi}{2},−\dfrac{\pi}{2},\dfrac{\pi}{2},\dfrac{3\pi}{2},\dfrac{5\pi}{2},\dfrac{7\pi}{2}\).

Revisar
1. Boceto\(p(x)=\sin x\) desde la memoria.
2. Boceto\(j(x)=\cos x\) desde la memoria.
3. ¿Dónde ocurren los máximos de la gráfica de coseno?
4. ¿Dónde ocurren los mínimos de la gráfica de coseno?
5. Encuentra todos los ceros de la función sinusoidal en el intervalo\(\left[−\pi ,\dfrac{5\pi}{2}\right]\).
6. Encuentra todos los ceros de la función coseno en el intervalo\(\left(−\dfrac{\pi}{2}, \dfrac{7\pi}{2}\right]\).
7. Vista previa: usando tu conocimiento de las transformaciones de funciones y la gráfica coseno, predice cómo\(f(x)=2\cos x\) será la gráfica de.
8. Vista previa: usando tu conocimiento de las transformaciones de funciones y la gráfica coseno, predice cómo será la gráfica\(g(x)=\cos x+2\) de.
9. Vista previa: usando tu conocimiento de las transformaciones de funciones y la gráfica coseno, predice cómo\(h(x)=\cos (x−\pi )\) será la gráfica de.
10. Vista previa: usando tu conocimiento de las transformaciones de funciones y la gráfica coseno, predice cómo\(k(x)=−\cos x\) será la gráfica de.
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 5.2.
El vocabulario
| Término | Definición |
|---|---|
| coseno | El coseno de un ángulo en un triángulo rectángulo es un valor que se encuentra dividiendo la longitud del lado adyacente al ángulo dado por la longitud de la hipotenusa. |
| seno | El seno de un ángulo en un triángulo rectángulo es un valor que se encuentra dividiendo la longitud del lado opuesto al ángulo dado por la longitud de la hipotenusa. |
| familia de funciones sinusoidales | La familia de funciones sinusoidales se refiere a ondas sinusoidales o cosenoidales ya que son las mismas excepto por un desplazamiento horizontal. Esta familia de funciones también se llama familia de funciones periódicas porque la función se repite después de un período de tiempo determinado. |
| Transformaciones | Las transformaciones se utilizan para cambiar la gráfica de una función padre en la gráfica de una función más compleja. |
| círculo de unidad | El círculo unitario es un círculo de radio uno, centrado en el origen. |
| Ceros | Los ceros de una función\(f(x)\) son los valores de\(x\) esa causa\(f(x)\) para ser igual a cero. |
Recursos adicionales
Video: Transformación de Gráficas Trigonométricas: Amplitud, Periodo y Desplazamiento de Fase
Mundo real: Banding Together

