2.7.4: Gráficas sinusoidales y cosecantes

Onda basada en el valor y y radio de un círculo; gráfica basada en el recíproco.

Gráficas sinusoidales y cosecantes

Imagina por un momento que tienes un reloj que tiene una sola mano, ¡que gira en sentido antihorario! No obstante, la mano es muy delgada hasta la punta, donde hay una bola al final. De hecho, la mano es tan delgada que no la notarás. Solo notas la bola en el extremo de la mano giratoria. Esta mano está girando más rápido de lo normal. Aquí hay una foto del reloj:

Figura\(\PageIndex{1}\)

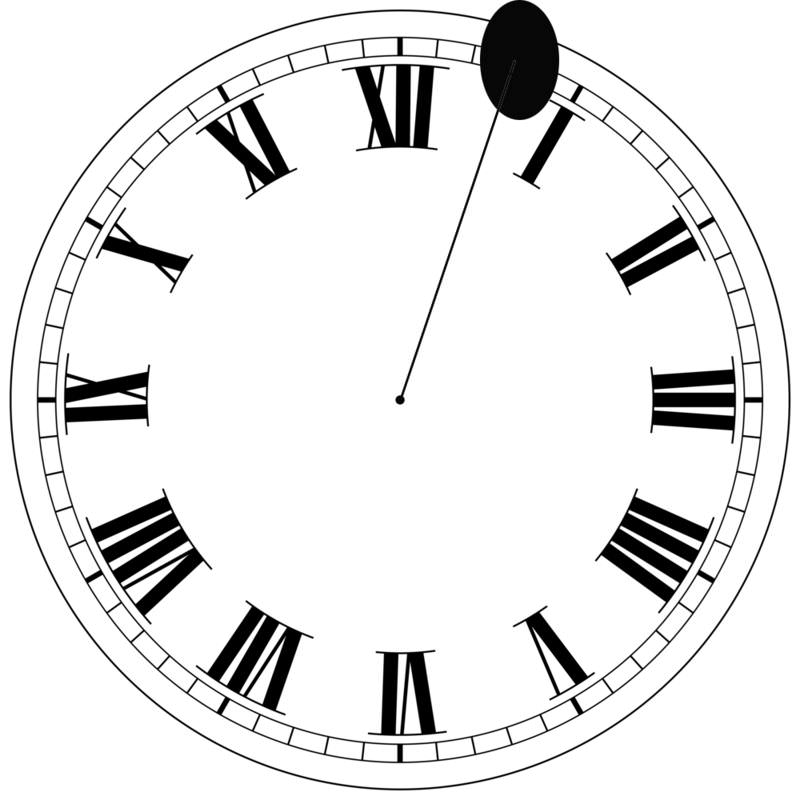
Considera cómo sería si pones una luz al lado del reloj y dejas que la sombra de las manecillas caiga sobre la pared del fondo.

¿Qué patrón trazaría esa sombra? Si lo piensas, podrías darte cuenta de que la sombra haría un movimiento hacia arriba y hacia abajo, una y otra vez a medida que giraba la manecilla del reloj. Ahora imagina que en lugar de una pared, había un gran trozo de papel para que cayera la sombra. Y donde quiera que cayera la sombra, habría una marca en el papel. Por último, imagínese mover el papel a medida que gira el reloj. ¿Te imaginas una especie de patrón que esto trazaría?

Gráficas sinusoidales y cosecantes

A estas alturas, ya se ha familiarizado con los valores específicos de seno, coseno y tangentes para ciertos ángulos de rotación alrededor de la cuadrícula de coordenadas. En matemáticas, a menudo podemos aprender mucho al observar cómo cambia una cantidad a medida que variamos constantemente otra. Estaremos viendo el valor sinusoidal como una función del ángulo de rotación alrededor del plano de coordenadas. Nos referimos a cualquiera de tales funciones como una función circular, ya que pueden definirse usando el círculo unitario. Recordemos de secciones anteriores que el seno de un ángulo en posición estándar es la relación de\(\dfrac{y}{r}\), donde\(y\) está la\(y\) coordenada −de cualquier punto del círculo y\(r\) es la distancia desde el origen hasta ese punto.

Figura\(\PageIndex{2}\)

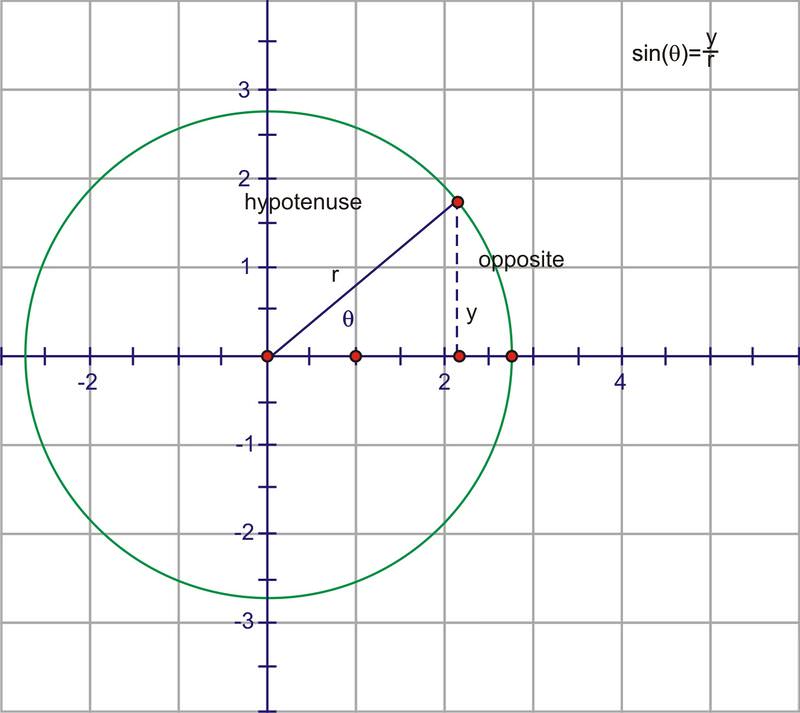
Debido a que las relaciones son las mismas para un ángulo dado, independientemente de la longitud del radio r, podemos usar el círculo unitario como base para todos los cálculos.

Figura\(\PageIndex{3}\)

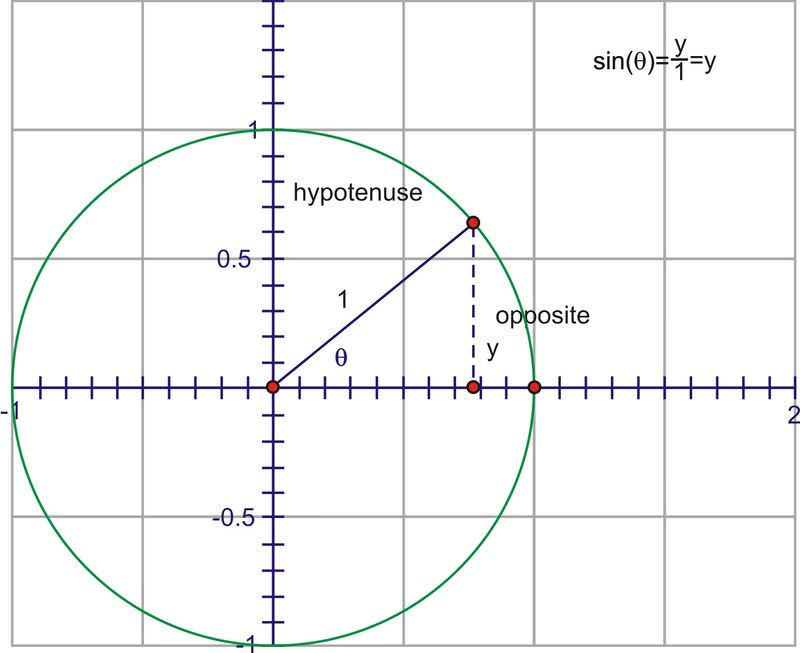
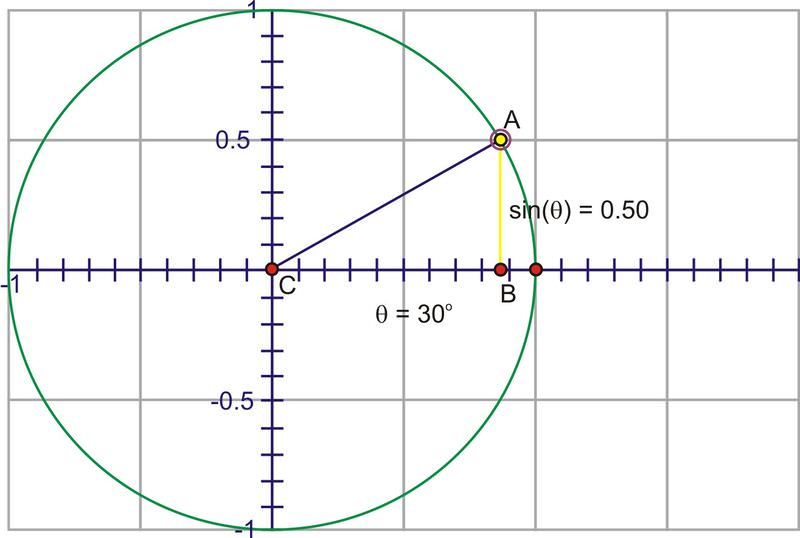
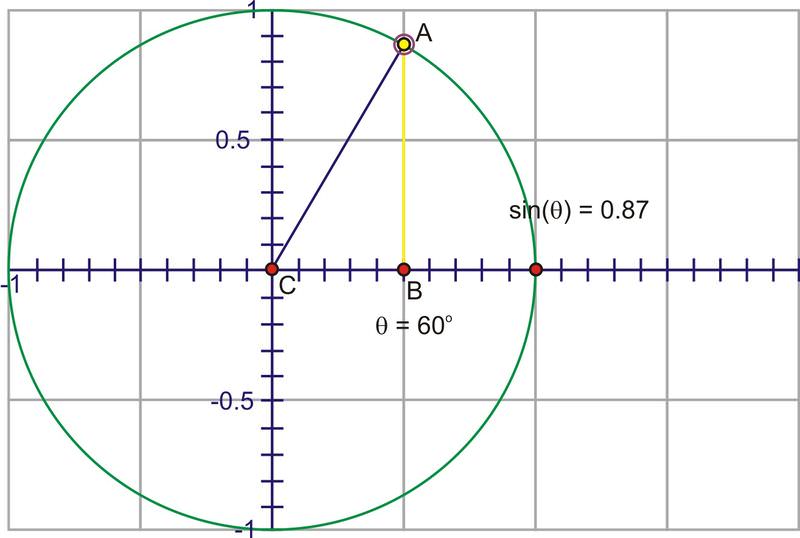
El denominador es ahora 1, así que tenemos la expresión más simple,\(\sin x=y\). La ventaja de esto es que podemos usar la coordenada y del punto en el círculo unitario para trazar el valor de\(\sin \theta \) a través de una rotación completa. Imagínese si empezamos en 0 y luego giramos en sentido antihorario a través de ángulos gradualmente crecientes. Dado que la coordenada y es el valor sinusoidal, observe la altura del punto a medida que gira.

A través del Cuadrante I esa altura se hace mayor, comenzando en 0, aumentando rápidamente al principio, luego más lenta hasta que el ángulo alcanza\(90^{\circ}\), en cuyo punto, la altura está en su valor máximo, 1.

Figura\(\PageIndex{4}\)

Figura\(\PageIndex{5}\)

Figura\(\PageIndex{6}\)

Figura\(\PageIndex{7}\)

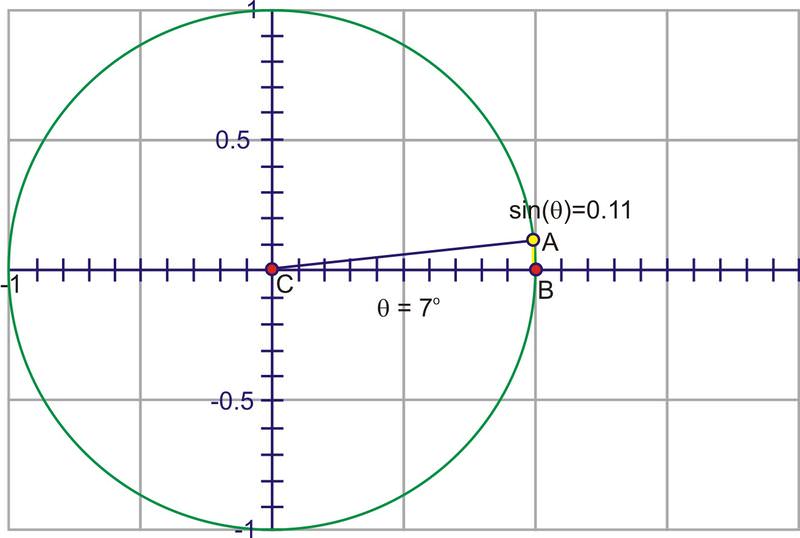
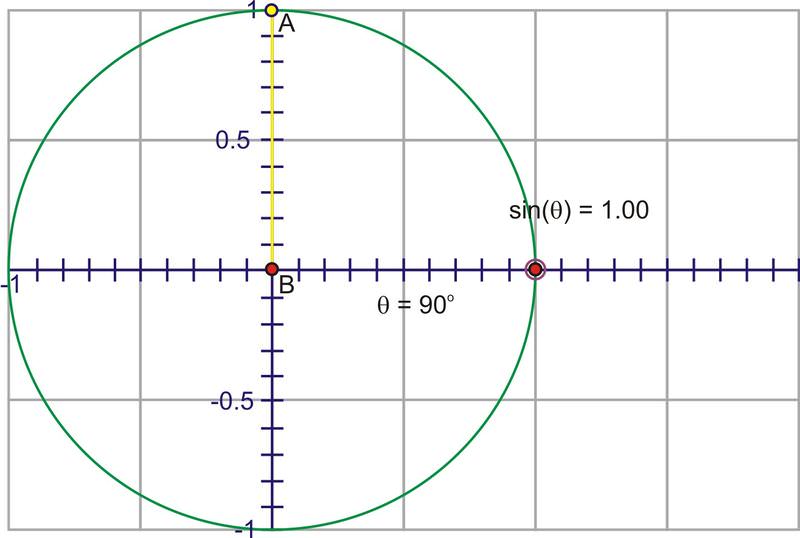
A medida que gira hacia el segundo cuadrante, la altura comienza a disminuir hacia cero.

Figura\(\PageIndex{8}\)

Figura\(\PageIndex{9}\)

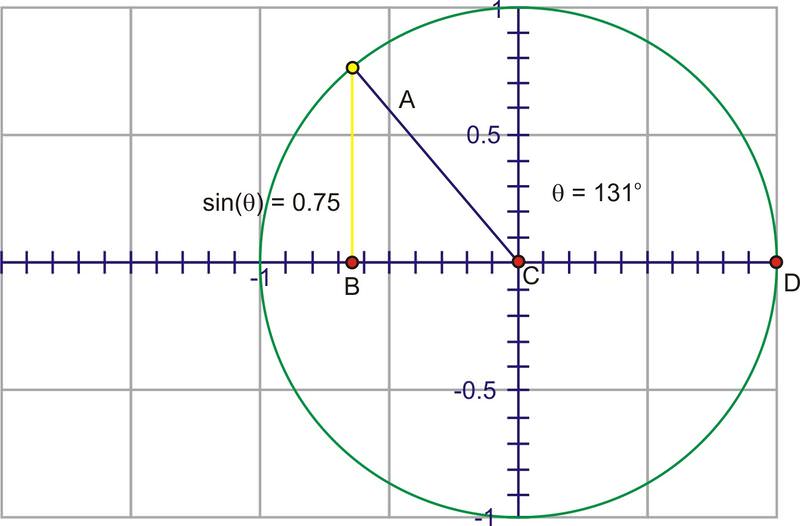
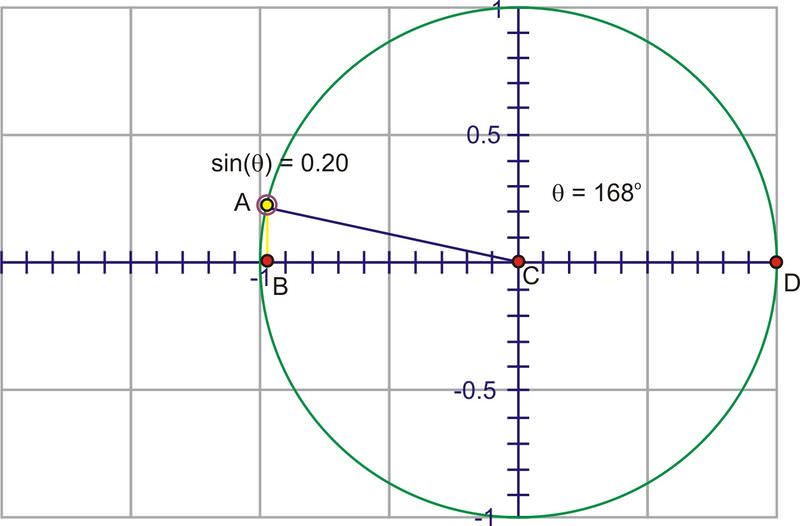
Cuando comienzas a rotar hacia el tercer y cuarto cuadrantes, la longitud del segmento aumenta, pero esta vez en una dirección negativa, creciendo a -1 en\(270^{\circ}\) y volviendo hacia 0 en\(360^{\circ}\).

Figura\(\PageIndex{10}\)

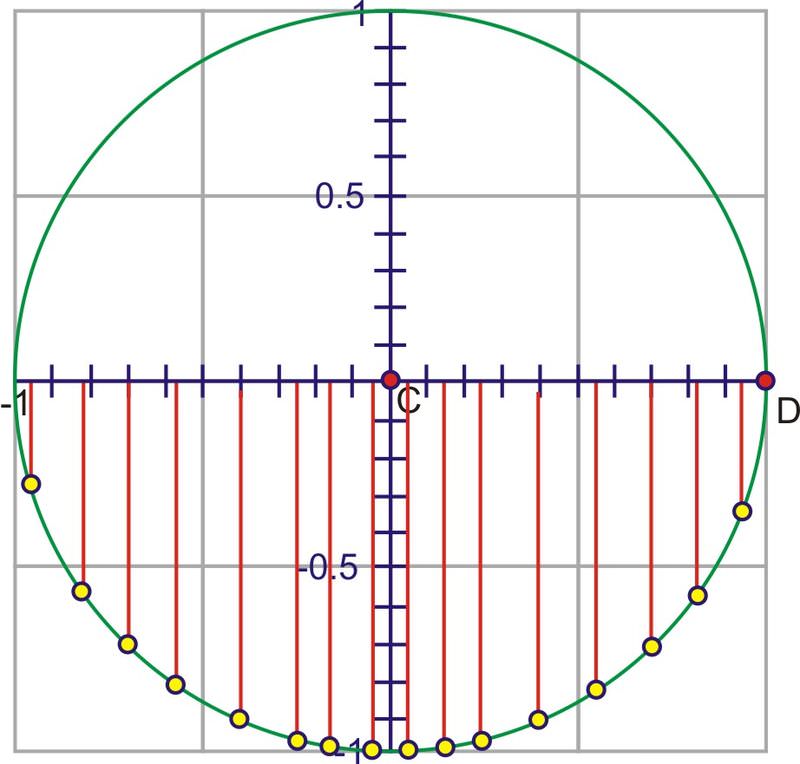
Después de una rotación completa, aunque el ángulo continúe aumentando, los valores sinusoidales se repetirán. Lo mismo habría sido cierto si optamos por rotar en el sentido de las agujas del reloj para investigar ángulos negativos, y es por ello que la función sinusoidal es una función periódica. El periodo es\(2\pi \) porque esa es la medida del ángulo antes de que el seno del ángulo repita sus valores.

Traduzcamos este movimiento circular en una gráfica del valor sinusoidal vs. el ángulo de rotación. La siguiente secuencia de imágenes demuestra la conexión. Estas imágenes se trazan\((\theta, \sin \theta )\) en el plano de coordenadas como\((x,y)\).

Figura\(\PageIndex{11}\)

Figura\(\PageIndex{12}\)

Figura\(\PageIndex{13}\)

Figura\(\PageIndex{14}\)

Figura\(\PageIndex{15}\)

Figura\(\PageIndex{16}\)

Figura\(\PageIndex{17}\)

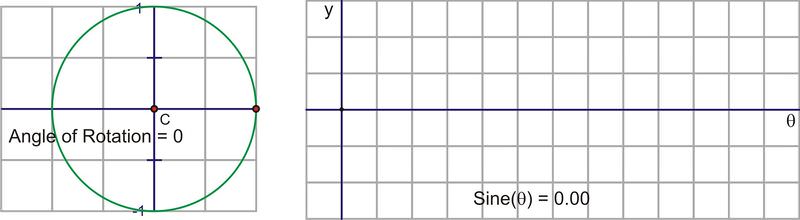
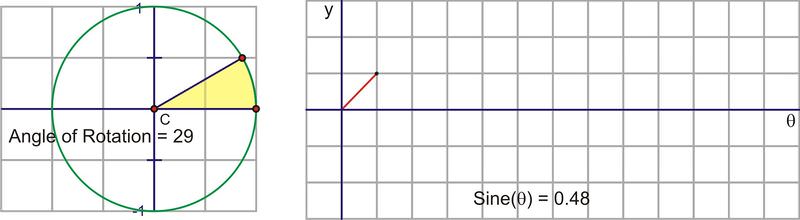
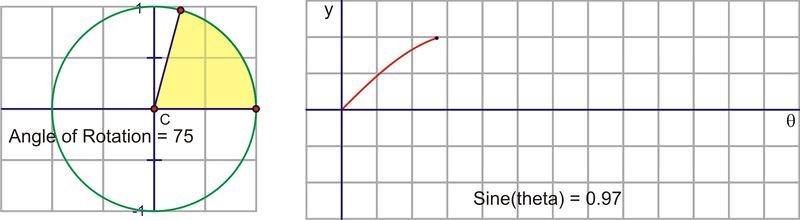
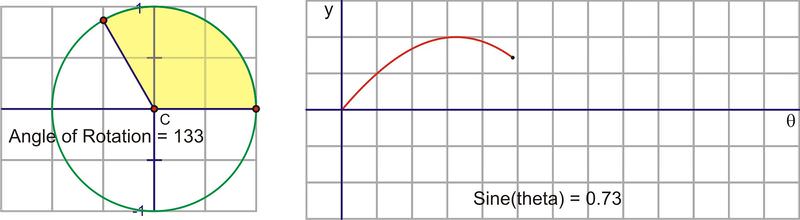
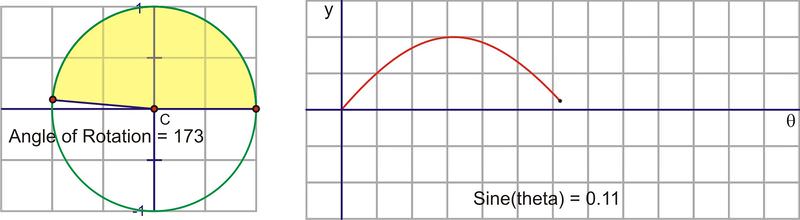
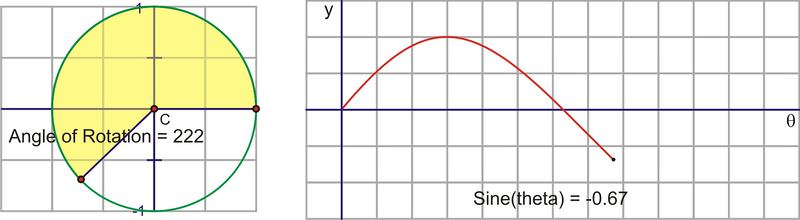
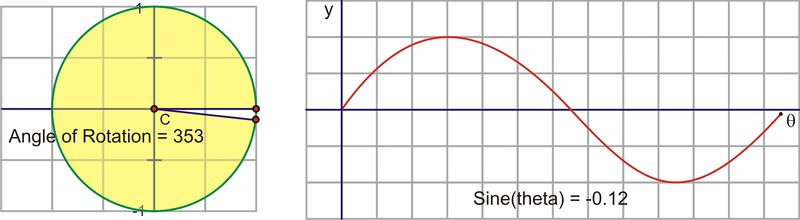
Después de que giramos alrededor del círculo una vez, los valores comienzan a repetirse. Por lo tanto, la curva sinusoidal, o “onda”, también continúa repitiéndose. La forma más fácil de esbozar una curva sinusoidal es trazar los puntos para los ángulos del cuadrante. El valor de\(\sin \theta \) va de 0 a 1 a 0 a -1 y de nuevo a 0. Graficado a lo largo de un eje horizontal, se vería así:

Figura\(\PageIndex{18}\)

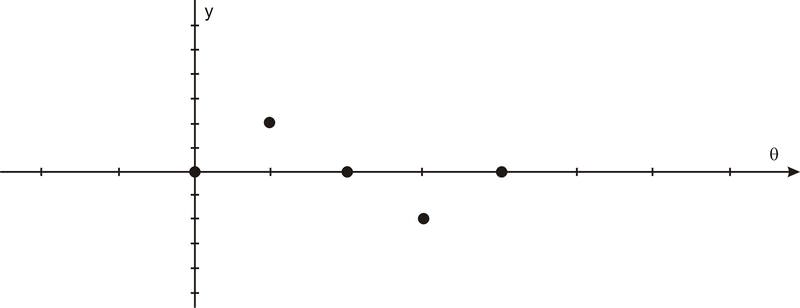
Llenar los huecos intermedios y permitir múltiples rotaciones así como ángulos negativos da como resultado la gráfica de\(y=\sin x\) dónde\(x\) está cualquier ángulo de rotación, en radianes.

Figura\(\PageIndex{19}\)

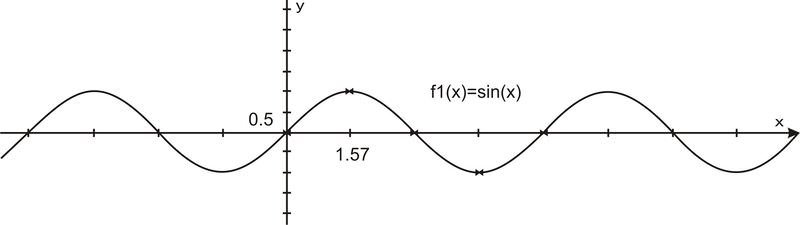
Como ya hemos mencionado,\(\sin x\) tiene un periodo de\(2\pi \). También debe tener en cuenta que los valores y−nunca van por encima de 1 o por debajo de -1, por lo que el rango de una curva sinusoidal es\(\{−1\leq y\leq 1\}\). Debido a que los ángulos pueden ser de cualquier valor y continuarán girando alrededor del círculo infinitamente, no hay restricción en el ángulo\(x\), por lo que el dominio de\(\sin x\) es todo real.

Cosecante es el recíproco de seno, o 1y. Por lo tanto, siempre que el seno sea cero, el cosecante va a tener una asíntota vertical porque quedará indefinida. También tiene el mismo signo que la función sinusoidal en los mismos cuadrantes. Aquí está la gráfica.

Figura\(\PageIndex{20}\)

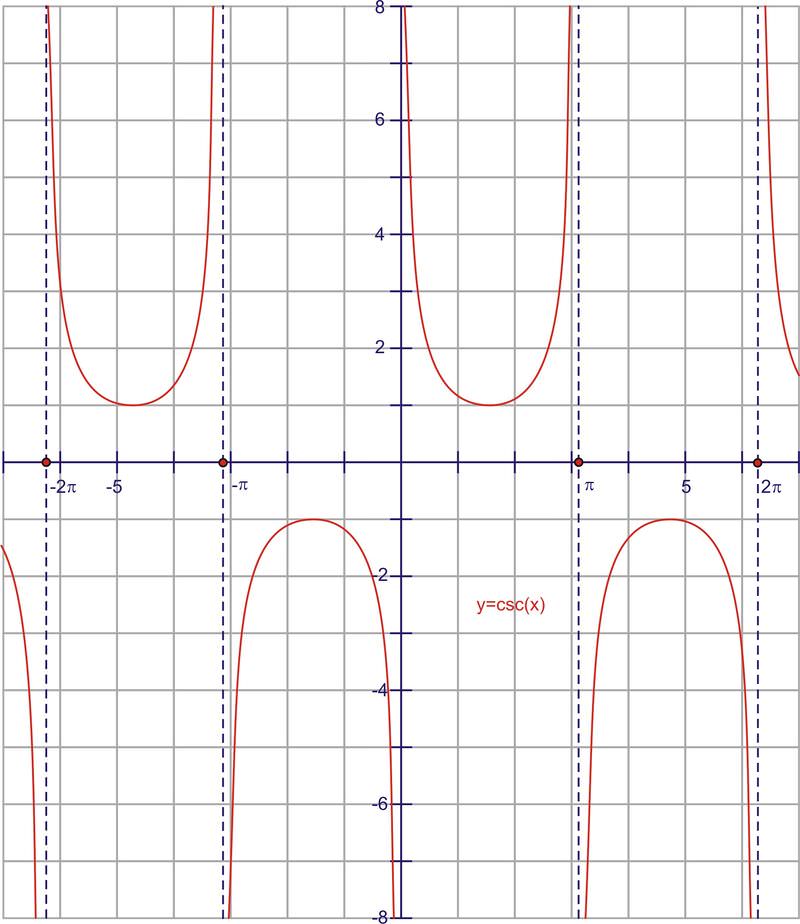
El periodo de la función es\(2\pi \), igual que seno. El dominio de la función es todos los números reales, excepto los múltiplos de\(\pi \left\{\ldots−2\pi ,−\pi ,0,\pi ,2\pi \ldots \right\}\). El rango es todos los números reales mayores o iguales a 1, así como todos los números reales menores o iguales a -1. Observe que el rango es todo excepto donde se define el seno (que no sean los puntos en la parte superior e inferior de la curva sinusoidal

Figura\(\PageIndex{21}\)

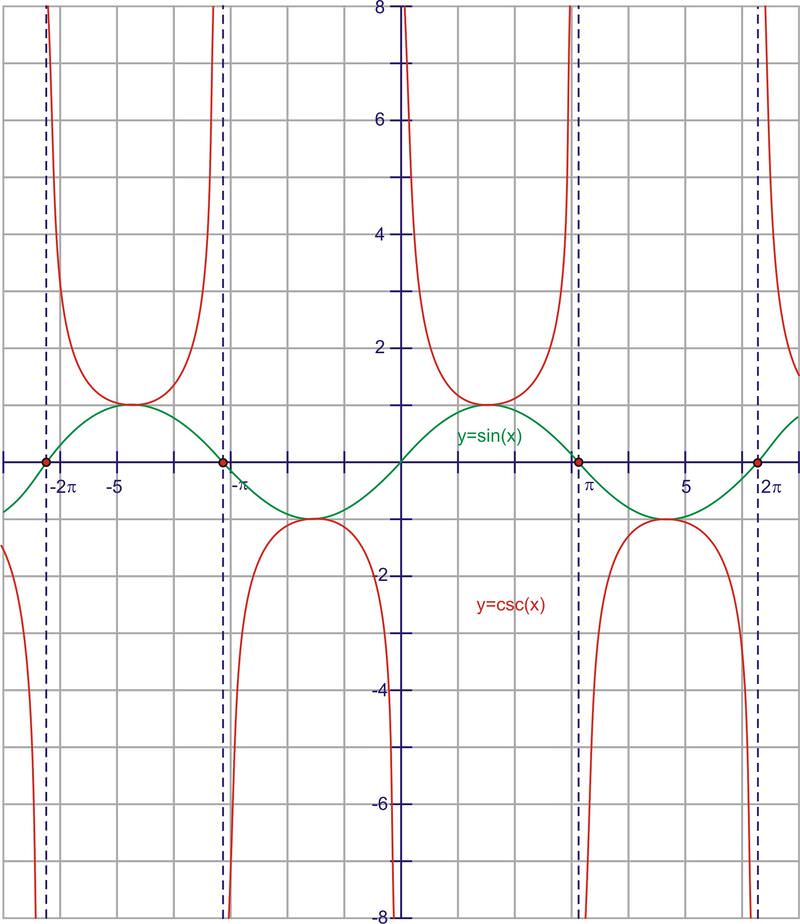
Observe nuevamente las relaciones recíprocas en 0 y las asíntotas. También observe los puntos de intersección de las gráficas en 1 y -1. A muchos estudiantes se les recuerda a las parábolas cuando miran el medio periodo de la gráfica cosecante. Si bien son similares en que cada uno tiene un mínimo o máximo local y tienen el mismo comportamiento inicial y final, las comparaciones terminan ahí. Las parábolas no están restringidas por asíntotas, mientras que la curva cosecante sí.

Funciones de Graficar

Grafica las siguientes funciones:

1. \(g(x)=\dfrac{1}{2}\sin (3x)\).

Figura\(\PageIndex{22}\)

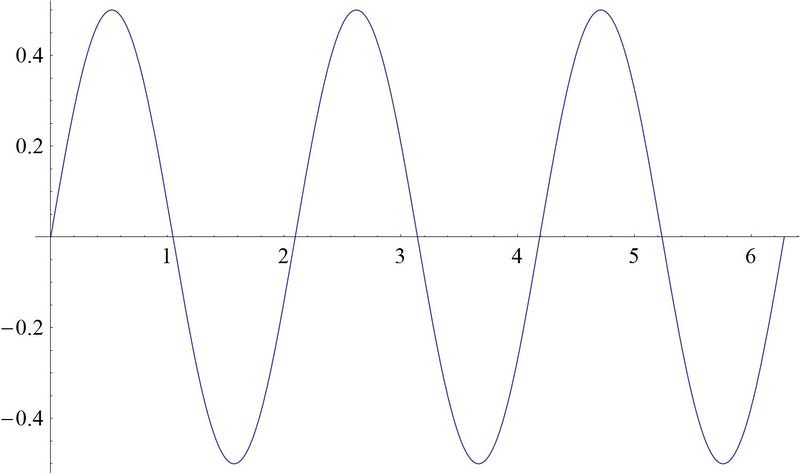
Como puede ver\(\dfrac{1}{2}\) en la gráfica, el frente de la función reduce la altura de la función, mientras que el 3 dentro del argumento de la función hace que la función sea “aplastada” a lo largo del eje “x”.

2. \(f(x)=\dfrac{1}{3} \csc\left(\dfrac{1}{2}x\right)\).

Figura\(\PageIndex{23}\)

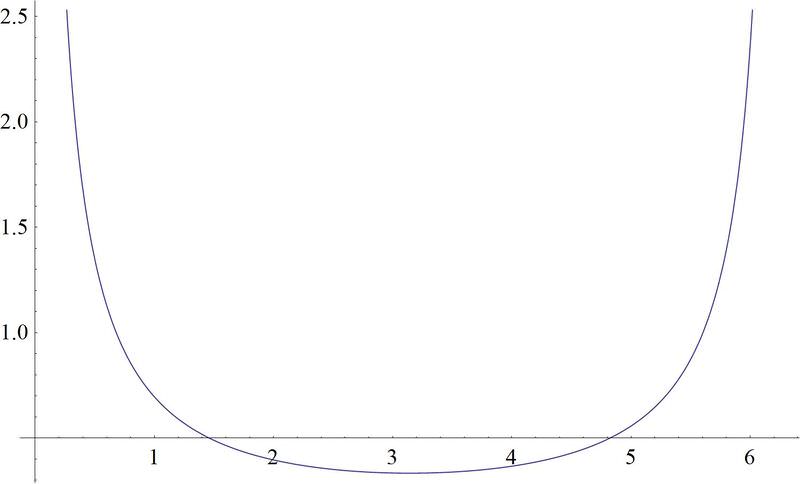
3. \(f(x)=5\sin \left(2\left(x+\dfrac{\pi }{3}\right)\right)\).

Figura\(\PageIndex{23}\)

Ejemplo\(\PageIndex{1}\)

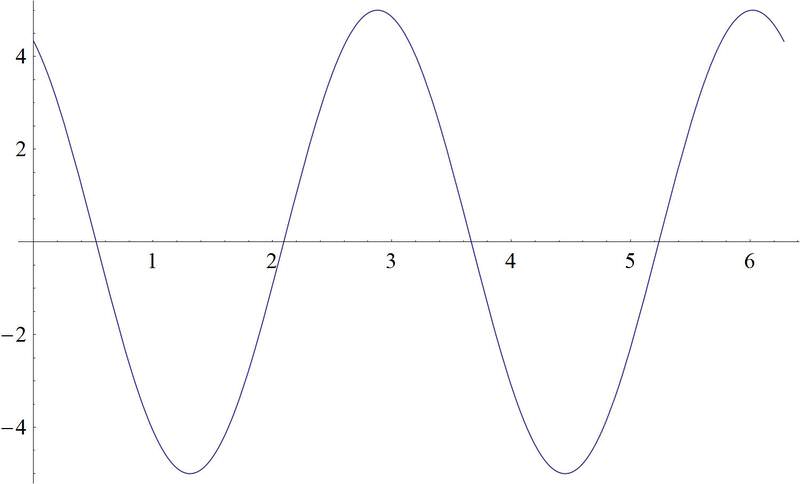
Anteriormente, se le preguntó qué patrón trazaría la sombra.

Solución

Como has visto en esta lección, la sombra de una luz aplicada verticalmente a una manecilla de reloj giratoria trazaría una gráfica sinusoidal. La gráfica empezaría en cero cuando la mano esté tendida plana a lo largo del eje “x” positivo. Posteriormente aumentaría hasta que la mano estuviera vertical. Entonces disminuiría hasta que la mano giratoria estuviera apuntando recto hacia abajo. Por último, la gráfica volvería a aumentar a cero cuando la mano regrese al eje “x” positivo.

Ejemplo\(\PageIndex{2}\)

Gráfica\(g(x)=5\csc\left(\dfrac{1}{4}\left(x+\pi \right)\right)\).

Solución

Figura\(\PageIndex{24}\)

Ejemplo\(\PageIndex{3}\)

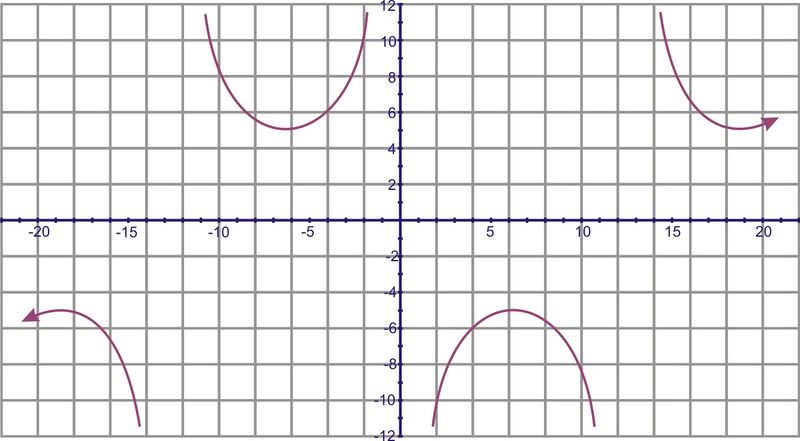
Determine la función que crea esta gráfica:

Figura\(\PageIndex{25}\)

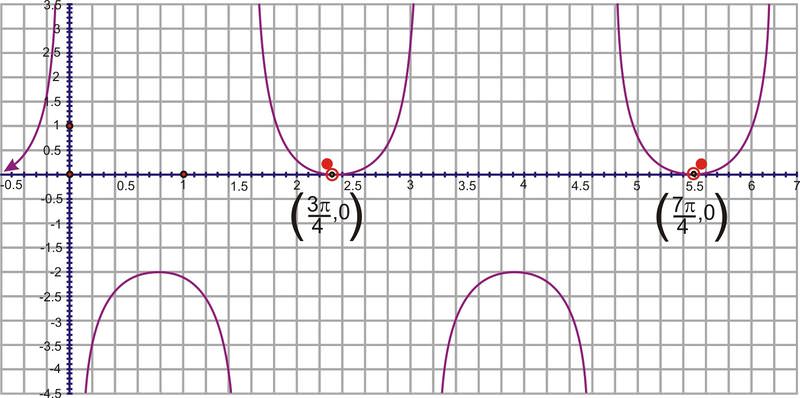
Solución

Esto podría ser una función secante o cosecante. Utilizaremos un modelo cosecante. En primer lugar, el desplazamiento vertical es -1. El periodo es la diferencia entre los dos valores x dados\(\dfrac{7 \pi}{4}−\dfrac{3 \pi}{4}=\pi \), así que la frecuencia es\(\dfrac{2\pi }{\pi }=2\). El desplazamiento horizontal incorpora la frecuencia, por lo que en\(y=\csc x\) el valor x correspondiente a\(\left(\dfrac{3 \pi}{4},0\right)\) es\(\left(\dfrac{\pi }{2},1\right)\). La diferencia entre los x−valores es\(\dfrac{3 \pi}{4}−\dfrac{\pi }{2}=3\dfrac{\pi}{4}−\dfrac{2 \pi}{4}=\dfrac{\pi}{4}\) y luego se multiplica por la frecuencia,\(2\cdot \dfrac{\pi}{4}=\dfrac{\pi }{2}\). La ecuación es\(y=−1+\csc \left(2\left(x−\dfrac{\pi }{2}\right)\right)\).

Ejemplo\(\PageIndex{4}\)

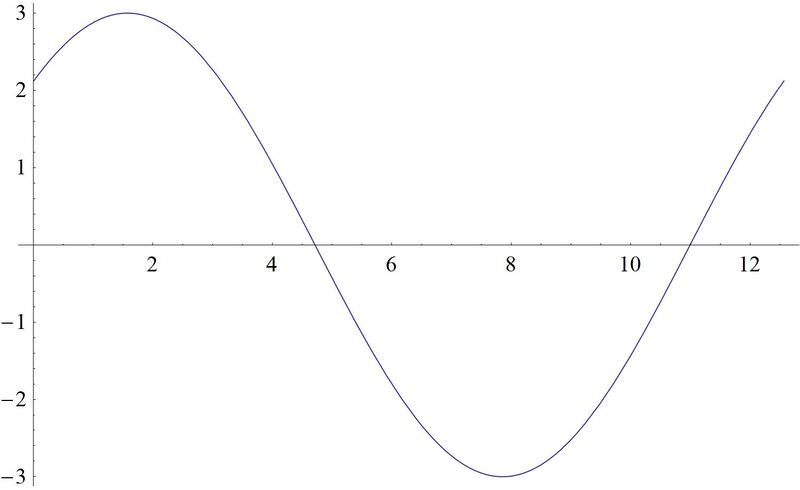
Gráfica\(h(x)=3\sin \left(\dfrac{1}{2}\left(x+\dfrac{\pi }{2}\right)\right)\).

Solución

Figura\(\PageIndex{26}\)

Revisar

Grafica cada una de las siguientes funciones.

1. \(f(x)=\sin (x)\).
2. \(h(x)=\sin (2x)\).
3. \(k(x)=\sin (2x+\pi )\).
4. \(m(x)=2\sin (2x+\pi )\).
5. \(g(x)=2\sin (2x+\pi )+2\).
6. \(f(x)=\csc(x)\).
7. \(h(x)=\csc(2x)\).
8. \(k(x)=\csc(2x+\pi )\).
9. \(m(x)=2\csc(2x+\pi )\).
10. \(g(x)=2\csc(2x+\pi )+2\).
11. \(h(x)=\sin (3x)\).
12. \(k(x)=\sin \left(3x+\dfrac{\pi }{2}\right)\).
13. \(m(x)=3\sin \left(3x+\dfrac{\pi }{2}\right)\).
14. \(g(x)=3\sin \left(3x+\dfrac{\pi }{2}\right)+3\).
15. \(h(x)=\csc(3x)\)
16. \(k(x)=\csc\left(3x+\dfrac{3 \pi }{2}\right)\).
17. \(m(x)=4\csc\left(3x+\dfrac{3 \pi }{2}\right)\).
18. \(g(x)=4\csc\left(3x+\dfrac{3 \pi }{2}\right)−3\).

Reseña (Respuestas)

Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 2.9.

El vocabulario

Término	Definición
Función Circular	Una función circular es una función medida al examinar el ángulo de rotación alrededor del plano de coordenadas.

Recursos adicionales

Video: Animación: Graficando la función sinusoidal U\ sin g el círculo unitario