4.1.2: Ley de los senos
- Page ID
- 107644
Proporción basada en proporciones de lados y senos de los ángulos opuestos para triángulos no rectos.
Cuando se le da un triángulo rectángulo, puede utilizar la trigonometría básica para resolver la información faltante. Cuando se le da SSS o SAS, puede utilizar la Ley de Cosinos para resolver la información faltante. Pero, ¿qué sucede cuando te dan dos lados de un triángulo y un ángulo que no está incluido? Hay muchas maneras de mostrar que dos triángulos son congruentes, pero SSA no es uno de ellos. ¿Por qué no?
La ley de los senos
Cuando se le dan dos lados y un ángulo que no se incluye entre los dos lados, se puede utilizar la Ley de los Sines. La Ley de Sines establece que en cada triángulo la relación de cada lado al\ pecado e de su ángulo correspondiente es siempre la misma. Esencialmente, aclara el concepto general de que frente al ángulo más grande es siempre el lado más largo.
a\ sin a=b\ sin b=C\ sin C
Aquí hay una prueba de la Ley de los Sines:
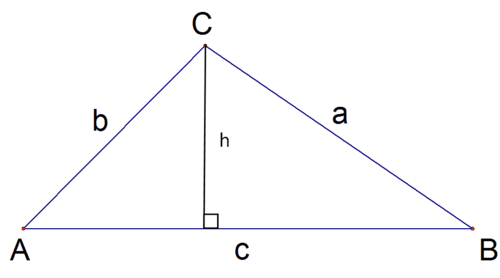
Mirando el triángulo derecho formado a la izquierda:
\(\begin{aligned} \sin A &=\dfrac{h}{b}\\ h&=b\sin A\end{aligned}\)
Mirando el triángulo rectángulo formado a la derecha:
\(\begin{aligned} \sin B &=\dfrac{h}{a}\\ h&=a\sin B \end{aligned}\)
Equiparando las alturas que deben ser idénticas:
\(\begin{aligned} a\sin B&=b\sin A \\ \dfrac{a}{\sin A}&=\dfrac{b}{\sin B} \end{aligned}\)
La mejor manera de usar la Ley de los Sines es dibujar una imagen extremadamente consistente en todas y cada una de las veces, aunque eso signifique volver a dibujar y volver a etiquetar una imagen. La razón por la que la consistencia es importante es porque a veces dada la información de SSA define cero, uno o incluso dos triángulos posibles.
Dibuja siempre el ángulo dado en la parte inferior izquierda con los dos lados dados arriba.
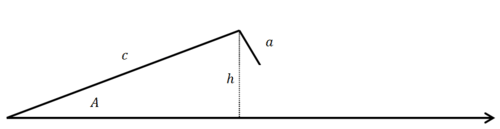
En esta imagen el lado a es deliberadamente demasiado corto, pero en la mayoría de los problemas no lo sabrás. Necesitarás comparar a con la altura.
\(\begin{aligned} \sin A &=\dfrac{h}{c}\\ h&=c \sin A\end{aligned}\)
Esto se refiere comúnmente a probar el caso ambiguo. Existen cuatro pruebas diferentes para determinar el número de triángulos que existen dadas las mediciones.
Caso 1:\(a<h\)
En pocas palabras, el lado a no es lo suficientemente largo para llegar al lado opuesto y construir el triángulo es imposible. Existen triángulos cero.
Caso 2:\(a=h\)
El lado a apenas alcanza el lado opuesto formando un ángulo de 90^ {\ circ}.
Caso 3:\(h<a<c\)
En este caso lado a puede oscilar hacia el interior del triángulo o el exterior del triángulo- hay dos triángulos posibles. Esto se llama el caso ambiguo porque la información dada no identifica de manera única un triángulo. Para resolver para ambos triángulos, use la Ley de Sines para resolver\(C_1\) primero el ángulo y luego use el suplemento para determinar\(C_2\).
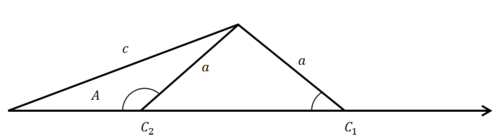
Caso 4:\(c\leq a\)
En este caso, el lado a solo puede oscilar hacia el exterior del triángulo, solo produciendo\(C_1\).
Para el caso de SSA, siempre se debe verificar cuántos triángulos hay antes de comenzar a encontrar medidas. Toma el siguiente triángulo:
\(\angle A=40^{\circ}\),\(c=13\), y\(a=2\).
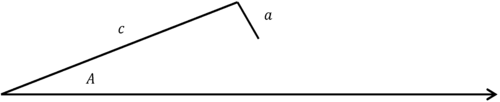
Antes de intentar encontrar\(\angle C\), es necesario verificar que un triángulo sea posible y si hay más de una solución. Usa la ecuación de arriba,
\(\begin{aligned} \sin 40^{\circ} &=\dfrac{h}{13}\\ h&=13\sin 40^{\circ}\approx 8.356 \end{aligned}\)
Debido a que a<h (2<8.356), esta información no forma un triángulo propio.
Anteriormente, se le preguntó por qué SSA no es un método para demostrar que dos triángulos son congruentes.
Solución
SSA no es un método de Geometría que muestre que dos triángulos son congruentes porque no siempre define un triángulo único. A veces no hay triángulo, ni un triángulo, ni dos triángulos.
\(\angle A=17^{\circ}\),\(c=14\), y\(a=4.0932 \ldots\) Si es posible, encuentra\(\angle C\).

Solución
Comprueba que un triángulo es posible:
\(\begin{aligned} \sin 17^{\circ} &=\dfrac{h}{14}\\ h&=14 \sin 17^{\circ}\approx 4.0932 \end{aligned}\)
Ya que\(a=h\), esta información forma exactamente un triángulo y el ángulo C debe ser\(90^{\circ}\).
\(\angle A=22^{\circ}\),\(c=11\) y\(a=9\). Si es posible, encuentra\(\angle C\).

Solución
Comprueba que un triángulo es posible:
\(\begin{aligned} \sin 22^{\circ} &=\dfrac{h}{11}\\ h&=11 \sin 22^{\circ}\approx 4.12 \end{aligned}\)
Ya que\(h<a<c\), debe haber dos ángulos posibles para el ángulo C.
Aplicar la Ley de los Sinos:
\ (\ begin {alineado}
\ frac {9} {\ sin 22^ {\ circ}} &=\ frac {11} {\ sin C_ {1}}\\
9\ sin C_ {1} &=11\ sin 22^ {\ circ}\
\ sin C_ {1} &=\ frac {11\ sin 22^ {\ circ}} {9}\
C_ {1} &=\ sin ^ {-1}\ izquierda (\ frac {11\ sin 22^ {\ circ}} {9}\ derecha)\ aprox. 27.24^ {\ circ}\\
C_ {2} &=180-C_ {1}\ aprox 152.75^ {\ circ}
\ final {alineado}\)
Dado\ Delta ABC donde A=12^ {\ circ},\(B=50^{\circ}\),\ (a=14 encontrar b.
Solución
\(\begin{aligned} \dfrac{14}{\sin 12^{\circ}}&=\dfrac{b}{\sin 50^{\circ}} \\ b&=\dfrac{14\sin 50^{\circ}}{\sin 12^{\circ}}\approx 51.58\end{aligned}\)
Dado\(\Delta ABC\) dónde\(A=70^{\circ}\),\(b=8\),\(a=3\), encontrar\(\angle B\) si es posible.
Solución
\(\begin{aligned} \sin 70^{\circ}&=\dfrac{h}{8} \\ h&=8\sin 70^{\circ}\approx 7.51 \ldots\end{aligned}\)
Porque\(a<h\), este triángulo es imposible.
Revisar
Para 1-3, dibuje una imagen del triángulo y establezca cuántos triángulos podrían formarse con los valores dados.
- \(A=30^{\circ}\),\(a=13\),\(b=15\)
- \(A=22^{\circ}\),\(a=21\),\(b=12\)
- \(A=42^{\circ}\),\(a=36\),\(b=37\)
Para 4-7, encuentre todas las medidas posibles de\ ángulo B (si existe alguna) para cada uno de los siguientes valores de triángulo.
- \(A=86^{\circ}\),\(a=15\),\(b=11\)
- \(A=30^{\circ}\),\(a=24\),\(b=43\)
- \(A=48^{\circ}\),\(a=34\),\(b=39\)
- \(A=80^{\circ}\),\(a=22\),\(b=20\)
Para 8-12, encuentre la longitud de b para cada uno de los siguientes valores de triángulo.
- \(A=94^{\circ}\),\(a=31\),\(B=34^{\circ}\)
- \(A=112^{\circ}\),\(a=12\),\(B=15^{\circ}\)
- \(A=78^{\circ}\),\(a=20\),\(B=16^{\circ}\)
- \(A=54^{\circ}\),\(a=15\),\(B=112^{\circ}\)
- \(A=39^{\circ}\),\(a=9\),\(B=98^{\circ}\)
- En\(\Delta ABC\),\(b=10\) y\(\angle A=39^{\circ}\). ¿Cuál es un valor posible para un que produciría dos triángulos?
- En\(\Delta ABC\),\(b=10\) y\(\angle A=39^{\circ}\). ¿Cuál es un valor posible para un que no produciría triángulos?
- En\(\Delta ABC\),\(b=10\) y\(\angle A=39^{\circ}\). ¿Cuál es un valor posible para un que produciría un triángulo?
Reseña (Respuestas)
Para ver las respuestas de Revisar, abra este archivo PDF y busque la sección 4.6.
vocabulario
| Término | Definición |
|---|---|
| ambiguo | Ambiguo significa que la información dada no es específica. En el contexto de la Geometría o Trigonometría, significa que los datos dados pueden no identificar de manera única una forma. |
| SSA | SSA significa lado, lado, ángulo y se refiere al hecho de que dos lados y el ángulo no incluido de un triángulo son conocidos en un problema. |
Recurso Adicional
Video: Resolver sistemas lineales multivariables - Descripción general
Práctica: Derecho de los Sines

